Dimension de Minkowski–Bouligand

Dimension de Minkowski–Bouligand
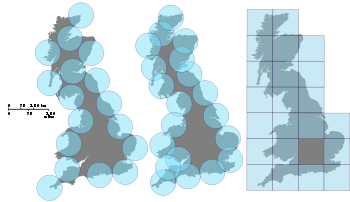
Recouvrement de la côte de Grande-Bretagne[1] par des réseaux carrés de maille décroissante

En géométrie fractale, la dimension de Minkowski–Bouligand, également appelée dimension de Minkowski ou dimension box-counting, est une manière de déterminer la dimension fractale d'un ensemble S dans un espace euclidien \scriptstyle{\mathbb{R}^n}, ou, plus généralement, un espace métrique (X,d).

Pour calculer cette dimension pour une fractale S, placer cette fractale dans un réseau carré et compter le nombre de cases nécessaires pour recouvrir l'ensemble. La dimension de Minkowski est calculée en observant comment ce nombre de cases évolue à mesure que le réseau s'affine à l'infini.

Supposons que N(ε) soit le nombre de cases de côté ε nécessaires pour recouvrir l'ensemble. Alors la dimension de Minkowski est définie par:

\dim_{\rm box}(S) := \lim_{\varepsilon \to 0} \frac {\log N(\varepsilon)}{\log (1/\varepsilon)}

Si la limite n'existe pas, alors on parle de dimension supérieure pour la limite supérieure et dimension inférieure pour la limite inférieure. En d'autres termes la dimension de Minkowski n'est bien définie que si ces deux valeurs sont égales. La dimension supérieure est parfois appelée dimension d'entropie, dimension de Kolmogorov ou notée upper box. La limite inférieure est parfois notée lower box.

Les deux sont fortement liées à la dimension de Hausdorff. Dans certains cas, ces trois valeurs sont différentes (voir plus bas pour plus de détails).

Sommaire

Types de recouvrement possibles

Trois types de recouvrements

La dimension de Minkowski reste identique pour les différents types de recouvrements pour lesquels N(ε) désigne[2]:

  • le nombre de cases de côté ε, sur un réseau carré, nécessaires pour recouvrir l'ensemble (à droite, sur l'illustration),
  • le plus petit nombre de boules de rayon ε couvrant l'ensemble (au milieu).
  • le plus petit nombre de cubes de côté ε couvrant l'ensemble.
  • le plus petit nombre d'ensembles de diamètre au plus ε couvrant l'ensemble.
  • le plus grand nombre de boules disjointes de rayon ε centrées sur l'ensemble (à gauche).

Définition par le voisinage

Une autre définition équivalente[2] de la dimension de Minkowski considère la façon dont le volume du voisinage de S décroit à mesure que ce voisinage rétrécit. Elle est donnée par la formule :

\dim_{box}(S) = n - \lim_{\varepsilon \to 0} \frac{\log \text{vol}(S_\varepsilon)}{\log \varepsilon},

où, pour tout \scriptstyle{\varepsilon>0}, l'ensemble \scriptstyle{S_\varepsilon} est défini comme le ε-voisinage de S, c'est-à-dire l'ensemble des points de \scriptstyle{\mathbb{R}^n} qui sont à une distance inférieure à ε de S. Ou, de manière équivalente, \scriptstyle{S_\varepsilon} est l'union de toutes les boules ouvertes de rayon ε centrées dans S.:

S_{\varepsilon} = \{x \in \mathbb{R}^n:|x-y|\le \varepsilon / y \in S\}

Propriétés

Les deux dimensions (upper et lower box) sont finiment additives, c'est-à-dire que si { A1, .... An } est une collection finie d'ensembles, alors

\dim (A_1 \cup \dotsb \cup A_n) = \max \{ \dim A_1 ,\dots, \dim A_n \}

Toutefois, cette propriété ne vaut pas pour une collection infinie d'ensembles. Par exemple, la dimension d'un point vaut 0. Mais la dimension de Minkowski des nombres rationnels sur l'intervalle [0, 1] a pour valeur 1.

Liens avec la dimension de Hausdorff

La dimension de Minkowski peut être vue comme la façon dont on peut recouvrir un ensemble avec de petits objets de même taille alors que la dimension de Hausdorff considère des recouvrements par des petits objets de taille variant, peut-être, de manière très significative. De plus, la dimension de Hausdorff s'appuie sur une mesure, ce qui n'est pas le cas pour la dimension de Minkowski, ce qui occasionne certaines propriétés jugées indésirables[2] (voir ci-dessous).

Malgré cela, la dimension de Minkowski est couramment utilisée pour la mesure d'objets fractals, car la mesure de Hausdorff est difficile à mettre en application.

Les dimensions de Minkowski et de Hausdorff sont égales pour nombre d’ensembles fractals, ceci est notamment conjecturé (Schroeder,1991) pour les ensembles fractals strictement auto-similaires. Par exemple, les dimensions de Hausdorff et de Minkowski de l’ensemble de Cantor sont égales à log(2) / log(3).

La dimension de Hausdorff et la dimension de Minkowski sont liées par l’inégalité suivante :

\dim_\operatorname{Haus} \leq \dim_\operatorname{lower box} \leq \dim_\operatorname{upper box}

En général, les inégalités sont strictes. en voici quelques exemples :

Exemple 1: La dimension de Minkowski supérieure peut être plus grande que la dimension inférieure si l’ensemble fractal a un comportement différent à différentes échelles. Par exemple, prenons l’intervalle [0,1] et examinons l’ensemble des nombres satisfaisant les conditions suivantes :

  • pour tout n, toutes les décimales entre la 22n-ème décimale et la (22n + 1 − 1)-ème décimale valent zéro ;
  • les décimales entre la 22n + 1 et 22n + 2 − 1 peuvent prendre n’importe quelle valeur.

Cette fractale a pour dimension supérieure 2/3 et pour dimension inférieure 1/3, un résultat qui peut être vérifié aisément en calculant N(ε) pour \varepsilon=10^{-2^n} et en remarquant que leur valeurs se comportent différemment pour n pair et impair. La dimension de Hausdorff, pour le même ensemble, vaut 0.

Exemple 2 : L’ensemble des nombres rationnels \scriptstyle{\mathbb{Q}}, un ensemble dénombrable avec \textstyle{\dim_\operatorname{Haus} = 0}, a pour dimension de Minkowski \textstyle{\dim_\operatorname{box} = 1} parce que sa clôture, \scriptstyle{\mathbb{R}}, a pour dimension 1.

Exemple 3 : La dimension de Minkowski manque également de propriétés de stabilité que l’on attendrait d’une dimension. Par exemple, on s’attendrait à ce que l’ajout d’un ensemble dénombrable n’ait aucun effet sur la valeur de la dimension. Cette propriété ne fonctionne pas pour la dimension de Minkowski. Ainsi :

\dim_\operatorname{box} \left\{0,1,\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \ldots\right\} = \frac{1}{2}.

Notes et références

  1. ↑ Le choix de cette côte a été proposé par Benoît Mandelbrot en 1967 pour illustrer le concept de dimension fractale.
  2. ↑ a, b et c (en) Kenneth Falconer, Fractal Geometry: Mathematical Foundations and Applications, Chichester, John Wiley & Sons, Ltd., 1990 & 2003, 2e éd., poche (ISBN 978-0-470-84862-3) (LCCN 2004271361), p. xxv 

Voir aussi

Liens externes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Dimension de Minkowski–Bouligand de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Dimension de Minkowski — Dimension de Minkowski–Bouligand En géométrie fractale, la dimension de Minkowski–Bouligand, également appelée dimension de Minkowski ou dimension box counting, est une manière de déterminer la dimension fractale d un ensemble S dans un Espace… …   Wikipédia en Français

  • Minkowski–Bouligand dimension — Estimating the box counting dimension of the coast of Great Britain In fractal geometry, the Minkowski–Bouligand dimension, also known as Minkowski dimension or box counting dimension, is a way of determining the fractal dimension of a set S in a …   Wikipedia

  • Minkowski-Bouligand dimension — In fractal geometry, the Minkowski Bouligand dimension, also known as Minkowski dimension or box counting dimension, is a way of determining the fractal dimension of a set S in a Euclidean space R^n, or more generally in a metric space ( X , d ) …   Wikipedia

  • Dimension box-counting — Dimension de Minkowski–Bouligand En géométrie fractale, la dimension de Minkowski–Bouligand, également appelée dimension de Minkowski ou dimension box counting, est une manière de déterminer la dimension fractale d un ensemble S dans un Espace… …   Wikipédia en Français

  • Dimension de Hamel — Dimension Voir « dimension » sur le Wiktionnaire …   Wikipédia en Français

  • Dimension spatiale — Dimension Voir « dimension » sur le Wiktionnaire …   Wikipédia en Français

  • Dimension fractale — Mesure de la dimension fractale de la côte de Grande Bretagne En géométrie fractale, la dimension fractale, D, est une grandeur qui a vocation à traduire la façon qu a un ensemble fractal de remplir l espace, à toutes les échelles. Dans le cas… …   Wikipédia en Français

  • Minkowski — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Personnes Hermann Minkowski (1864 1909), mathématicien et physicien théoricien allemand ; Oskar Minkowski (1858 1931), médecin allemand, frère du… …   Wikipédia en Français

  • Dimensión — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

  • Dimension topologique — En mathématiques, la dimension topologique est une notion destinée à étendre à des espaces métriques la notion algébrique de dimension d un espace vectoriel. Définition Soit E un espace métrisable à base dénombrable. On définit la dimension… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”