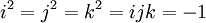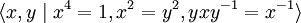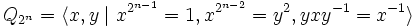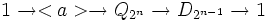Groupe quaternionique

Groupe quaternionique

Groupe de quaternions

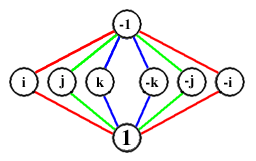Diagramme du cycle de Q. Chaque couleur précise une série de puissances d'un élément quelconque connecté à l'élément neutre (1). Par exemple, le cycle rouge reflète le fait que i 2 = -1, i 3 = -i  et i 4 = 1. Le cycle rouge reflète aussi le fait que (-i )2 = -1, (-i )3 = i  et (-i )4 = 1.

En mathématiques et dans théorie des groupes, le groupe des quaternions est un groupe non abélien d'ordre 8.

La représentation du groupe de quaternion irréductible de dimension quatre sur les nombres réels forme un corps gauche, c'est-à-dire non commutatif. Il est appelé corps des quaternions.

Sommaire

Définition

Le groupe des quaternions est souvent désigné par le symbole Q ou Q8 et est écrit sous forme multiplicative, avec les 8 éléments suivants :

Q = {1, -1, i, -i, j, -j, k, -k}\,

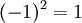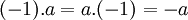Ici, 1 est l'élément neutre, (- 1)^2 = 1\, et ( - 1).a = a.(- 1) = - a\, pour tout a dans Q. Les règles de multiplication restantes peuvent être obtenues à partir de la relation suivante :

i^2 = j^2 = k^2 = ijk = -1\,

Table du groupe

La table de multiplication pour Q est donnée par :

1 i j k -1 -i -j -k
1 1 i j k -1 -i -j -k
i i -1 k -j -i 1 -k j
j j -k -1 i -j k 1 -i
k k j -i -1 -k -j i 1
-1 -1 -i -j -k 1 i j k
-i -i 1 -k j i -1 k -j
-j -j k 1 -i j -k -1 i
-k -k -j i 1 k j -i -1

Le groupe ainsi obtenu est non commutatif comme on peut le voir sur la relation ij = - ji\,. Cependant Q est un groupe hamiltonien : chaque sous-groupe de Q est un sous-groupe normal, mais le groupe est non abélien. Chaque groupe hamiltonien contient une copie de Q.

Propriétés

Représentation

Article détaillé : Représentations du groupe des quaternions.

Considérant un espace vectoriel réel de dimension quatre dont une base est notée {1, i, j, k}, on la munit d'une structure d'algèbre associative en utilisant la table de multiplication ci-dessus et la distributivité. Le résultat est un corps appelé les corps des quaternions. 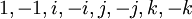Inversement, on peut démarrer avec les quaternions et définir le groupe des quaternions comme le sous-groupe multiplicatif constitué des 8 éléments {1, - 1, i, - i, j, - j, k, - k}\,.

La théorème d'Artin-Wedderburn généralise cette approche. Il permet, avec la théorie des représentations d'un groupe fini de construire des algèbres semi-simples contenant un corps gauche, c'est-à-dire non commutatif.

Nature du groupe

Les trois éléments i, j et k sont tous d'ordre 4 dans Q et deux quelconques d'entre eux engendrent le groupe entier. Q admet la présentation

\langle x,y \mid x^4 = 1, x^2 = y^2, yxy^{-1} = x^{-1}\rangle

On peut prendre, par exemple, x = i et y = j.

Le centre et le sous-groupe des commutateurs de Q est le sous-groupe {±1}. Le groupe quotient Q/{±1} est isomorphe au groupe de Klein V. Les classes de conjugaison sont au nombre de cinq : {1}, {-1}, {i, -i}, {j, -j} et {k, -k}.

Le groupe des automorphismes intérieurs de Q est isomorphe à Q modulo son centre, et est par conséquent aussi isomorphe au groupe de Klein. Le groupe des automorphismes de Q est isomorphe à S4, le groupe symétrique sur quatre lettres. Le groupe des automorphismes extérieurs de Q est alors S4/V qui est isomorphe à S3. Le groupe des quaternions Q peut être vu comme agissant sur les 8 éléments non nuls de l'espace vectoriel à 2 dimensions sur le corps fini F3. Pour une image, voir Visualisation de GL(2,p).

Groupe de quaternions généralisé

Un groupe est appelé un groupe de quaternions généralisé s'il possède une présentation

Q_{2^n}=\langle x,y \mid x^{2^{n-1}} = 1, x^{2^{n-2}} = y^2, yxy^{-1} = x^{-1}\rangle

pour un certain entier n ≥ 3. L'ordre de ce groupe est 2n. Le groupe de quaternions ordinaire correspond au cas n = 3. Le groupe de quaternions généralisé peut être réalisé comme le sous-groupe des quaternions unités engendré par

x = e^{2\pi i/2^{n-1}}
y = j\,

Un tel groupe peut être mis en relation avec un groupe diédral d'ordre 2n-1 par la suite exacte :

1\to <a>\to Q_{2^n}\to D_{2^{n-1}}\to 1

Les groupes de quaternions généralisés sont membres d'une famille encore plus large de groupes dicycliques. Les groupes de quaternions généralisés ont la propriété que chaque sous-groupe abélien est cyclique. Il peut être montré qu'un p-groupe fini avec cette propritété (chaque sous-groupe abélien est cyclique) est soit cyclique ou un groupe de quaternions généralisé comme défini ci-dessus.

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Groupe de quaternions ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Groupe quaternionique de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Groupe Sporadique — En mathématiques, un groupe sporadique est l un des 26 groupes exceptionnels dans la classification des groupes simples finis. Un groupe simple est un groupe G qui ne possède aucun sous groupe normal à part le sous groupe trivial réduit à l… …   Wikipédia en Français

  • Groupe Symplectique — En mathématiques, le terme groupe symplectique est utilisé pour désigner deux familles différentes de groupes linéaires. On les note Sp(2n, E) et Sp(n), ce dernier étant parfois nommé groupe compact symplectique pour le distinguer du premier.… …   Wikipédia en Français

  • Groupe symplectique linéaire — Groupe symplectique En mathématiques, le terme groupe symplectique est utilisé pour désigner deux familles différentes de groupes linéaires. On les note Sp(2n, E) et Sp(n), ce dernier étant parfois nommé groupe compact symplectique pour le… …   Wikipédia en Français

  • Groupe sporadique — En mathématiques, un groupe sporadique est l un des 26 groupes exceptionnels dans la classification des groupes simples finis. Un groupe simple est un groupe G non trivial qui ne possède aucun sous groupe normal à part son sous groupe trivial… …   Wikipédia en Français

  • Groupe symplectique — En mathématiques, le terme groupe symplectique est utilisé pour désigner deux familles différentes de groupes linéaires. On les note Sp(2n, E) et Sp(n), ce dernier étant parfois nommé groupe compact symplectique pour le distinguer du premier.… …   Wikipédia en Français

  • Structure presque quaternionique — En mathématiques, une structure presque quaternionique sur une variété différentielle réelle est une donnée visant à associer à son fibré tangent une structure d espace vectoriel sur le corps[1] des quaternions. Sa définition a varié depuis le… …   Wikipédia en Français

  • Théorème de Frattini — Pour les articles homonymes, voir Frattini. En mathématiques, en plus précisément en théorie des groupes, le théorème de Frattini permet de préciser la structure d une famille de groupes finis, appelée p groupes. Il stipule que le quotient d un p …   Wikipédia en Français

  • Holonomie — En mathématiques, et plus précisément en géométrie différentielle, l holonomie d une connexion sur une variété différentielle est une mesure de la façon dont le transport parallèle le long de boucles fermées modifie les informations géométriques… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Matrice (mathématiques) — Pour les articles homonymes, voir Matrice. En mathématiques, les matrices sont des tableaux de nombres qui servent à interpréter en termes calculatoires et donc opérationnels les résultats …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”