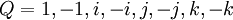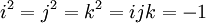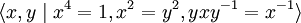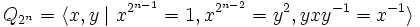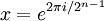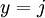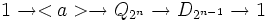Groupe quaternionien

Groupe quaternionien

Groupe de quaternions

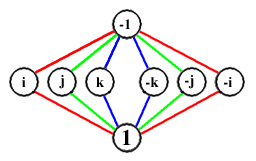Diagramme du cycle de Q. Chaque couleur précise une série de puissances d'un élément quelconque connecté à l'élément neutre (1). Par exemple, le cycle rouge reflète le fait que i 2 = -1, i 3 = -i  et i 4 = 1. Le cycle rouge reflète aussi le fait que (-i )2 = -1, (-i )3 = i  et (-i )4 = 1.

En mathématiques et dans théorie des groupes, le groupe des quaternions est un groupe non abélien d'ordre 8.

La représentation du groupe de quaternion irréductible de dimension quatre sur les nombres réels forme un corps gauche, c'est-à-dire non commutatif. Il est appelé corps des quaternions.

Sommaire

Définition

Le groupe des quaternions est souvent désigné par le symbole Q ou Q8 et est écrit sous forme multiplicative, avec les 8 éléments suivants :

Q = {1, -1, i, -i, j, -j, k, -k}\,

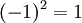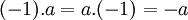Ici, 1 est l'élément neutre, (- 1)^2 = 1\, et ( - 1).a = a.(- 1) = - a\, pour tout a dans Q. Les règles de multiplication restantes peuvent être obtenues à partir de la relation suivante :

i^2 = j^2 = k^2 = ijk = -1\,

Table du groupe

La table de multiplication pour Q est donnée par :

1 i j k -1 -i -j -k
1 1 i j k -1 -i -j -k
i i -1 k -j -i 1 -k j
j j -k -1 i -j k 1 -i
k k j -i -1 -k -j i 1
-1 -1 -i -j -k 1 i j k
-i -i 1 -k j i -1 k -j
-j -j k 1 -i j -k -1 i
-k -k -j i 1 k j -i -1

Le groupe ainsi obtenu est non commutatif comme on peut le voir sur la relation 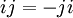ij = - ji\,. Cependant Q est un groupe hamiltonien : chaque sous-groupe de Q est un sous-groupe normal, mais le groupe est non abélien. Chaque groupe hamiltonien contient une copie de Q.

Propriétés

Représentation

Article détaillé : Représentations du groupe des quaternions.

Considérant un espace vectoriel réel de dimension quatre dont une base est notée {1, i, j, k}, on la munit d'une structure d'algèbre associative en utilisant la table de multiplication ci-dessus et la distributivité. Le résultat est un corps appelé les corps des quaternions. 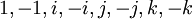Inversement, on peut démarrer avec les quaternions et définir le groupe des quaternions comme le sous-groupe multiplicatif constitué des 8 éléments {1, - 1, i, - i, j, - j, k, - k}\,.

La théorème d'Artin-Wedderburn généralise cette approche. Il permet, avec la théorie des représentations d'un groupe fini de construire des algèbres semi-simples contenant un corps gauche, c'est-à-dire non commutatif.

Nature du groupe

Les trois éléments i, j et k sont tous d'ordre 4 dans Q et deux quelconques d'entre eux engendrent le groupe entier. Q admet la présentation

\langle x,y \mid x^4 = 1, x^2 = y^2, yxy^{-1} = x^{-1}\rangle

On peut prendre, par exemple, x = i et y = j.

Le centre et le sous-groupe des commutateurs de Q est le sous-groupe {±1}. Le groupe quotient Q/{±1} est isomorphe au groupe de Klein V. Les classes de conjugaison sont au nombre de cinq : {1}, {-1}, {i, -i}, {j, -j} et {k, -k}.

Le groupe des automorphismes intérieurs de Q est isomorphe à Q modulo son centre, et est par conséquent aussi isomorphe au groupe de Klein. Le groupe des automorphismes de Q est isomorphe à S4, le groupe symétrique sur quatre lettres. Le groupe des automorphismes extérieurs de Q est alors S4/V qui est isomorphe à S3. Le groupe des quaternions Q peut être vu comme agissant sur les 8 éléments non nuls de l'espace vectoriel à 2 dimensions sur le corps fini F3. Pour une image, voir Visualisation de GL(2,p).

Groupe de quaternions généralisé

Un groupe est appelé un groupe de quaternions généralisé s'il possède une présentation

Q_{2^n}=\langle x,y \mid x^{2^{n-1}} = 1, x^{2^{n-2}} = y^2, yxy^{-1} = x^{-1}\rangle

pour un certain entier n ≥ 3. L'ordre de ce groupe est 2n. Le groupe de quaternions ordinaire correspond au cas n = 3. Le groupe de quaternions généralisé peut être réalisé comme le sous-groupe des quaternions unités engendré par

x = e^{2\pi i/2^{n-1}}
y = j\,

Un tel groupe peut être mis en relation avec un groupe diédral d'ordre 2n-1 par la suite exacte :

1\to <a>\to Q_{2^n}\to D_{2^{n-1}}\to 1

Les groupes de quaternions généralisés sont membres d'une famille encore plus large de groupes dicycliques. Les groupes de quaternions généralisés ont la propriété que chaque sous-groupe abélien est cyclique. Il peut être montré qu'un p-groupe fini avec cette propritété (chaque sous-groupe abélien est cyclique) est soit cyclique ou un groupe de quaternions généralisé comme défini ci-dessus.

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Groupe de quaternions ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Groupe quaternionien de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Groupe classique — En mathématiques, les groupes classiques sont différentes familles de groupes de transformations liées à l algèbre linéaire, principalement les groupes linéaires, orthogonaux, symplectiques et unitaires. Ces groupes peuvent aussi être présentés… …   Wikipédia en Français

  • Algèbre simple — En mathématiques, une algèbre (unitaire associative) sur un corps commutatif est dite simple si son anneau sous jacent est simple, c est à dire s il n admet pas d idéal bilatère autre que {0} et lui même, et si de plus il n est pas réduit à 0. Si …   Wikipédia en Français

  • Forme hermitienne — Cet article concerne le cas général abstrait. Pour un cas plus élémentaire, voir Forme sesquilinéaire complexe. En mathématiques, une forme hermitienne est une fonction de deux variable sur un espace vectoriel sur un corps relativement à une… …   Wikipédia en Français

  • Algèbre involutive simple — En mathématiques, une algèbre involutive simple sur un corps commutatif est une algèbre involutive qui n admet par d idéaux stable par l involution autre que {0} et elle même. Les algèbres involutives simples centrales (en un sens à préciser plus …   Wikipédia en Français

  • Algèbre involutive — En mathématiques, une algèbre involutive est une algèbre munie d une isomorphisme sur son algèbre opposée, et donc le carré est l identité. Dans cet article, K désigne un anneau commutatif, et les algèbres sur un anneau commutatif sont supposées… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”