Liste Des Groupes Finis Simples

Liste des groupes finis simples

En mathématiques, la classification des groupes finis simples établit que chacun de ces groupes est soit un cyclique, soit alterné, soit membre d'une des seize familles de groupes de type de Lie (incluant le groupe de Tits), soit l'un des 26 groupes sporadiques (le groupe de Tits est parfois inclus dans les groupes de type de Lie, d'autres fois dans les groupes sporadiques).

La liste ci-dessous recense les groupes finis simples en les organisant par famille et précise à chaque fois leur ordre, la taille de leur multiplicateur de Schur, celle de leur groupe d'automorphisme extérieur et éventuellement certaines représentations habituelles. Les groupes finis simples sont déterminés par leur ordre, excepté les groupes B_n(q) et C_n(q) dont l'ordre est identique pour n > 2 et q impair, et les groupes A₈ (ou A₃(2)) et A₂(4) dont l'ordre est 20 160.

À titre de notation, dans cette liste, n désigne un entier positif, p un nombre premier et q une puissance entière de p. L'ordre du groupe d'automorphisme extérieur est donné sous la forme d·f·g, où d est l'ordre du groupe des automorphismes diagonaux, f est celui du groupe d'automorphismes de corps (engendrés par un automorphisme de Frobenius) et g celui du groupe des automorphismes de graphe (provenant des automorphismes du diagramme de Dynkin).

Familles infinies

Groupes cycliques Z_p

Article détaillé : Groupe cyclique.

Notation: Z_p
Autres noms: Z/pZ
Simplicité: Toujours simples.
Ordre: p
Multiplicateur de Schur: Trivial.
Groupe d'automorphisme extérieur: Cyclique d'ordre p-1.
Remarque: Les groupes cycliques sont les seuls groupes simples qui ne sont pas parfaits.

Groupes alternés A_n

Article détaillé : Groupe alterné.

Notation: A_n, pour n > 4. Il existe un conflit avec la notation des groupes de type Lie A_n(q) qui n'ont aucun lien avec les groupes alternés ; certains auteurs utilisent des polices distinctes afin de les distinguer.
Autre noms: Alt_n.
Simplicité: Résolubles pour n < 5, simples dans le cas contraire.
Ordre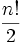: $\frac{n!}{2}$ pour n > 1.
Multiplicateur de Schur: 2 pour n = 5 ou n > 7, 6 pour n = 6 ou 7.
Groupe d'automorphisme extérieur: En général 2. Exceptions : pour n = 1, n = 2, il est trivial, et pour n = 6, il possède un ordre 4 (abélien élémentaire).
Isomorphismes

A₁ et A₂ sont triviaux. A₃ est cyclique d'ordre 3. A₄ est isomorphe à A₁(3) (résoluble). A₅ est isomorphe à A₁(4) et à A₁(5). A₆ est isomorphe à A₁(9)et au groupe dérivé B₂(2)′. A₈ est isomorphe à A₃(2).

Remarques: Un sous-groupe d'index 2 du groupe symétrique de permutations de n points lorsque n > 1.

Groupes classiques

Groupes de Chevalley linéaires A_n(q)

Article détaillé : Groupes de Chevalley.

Notation: A_n(q)
Autres noms: Groupes linéaires projectifs spéciaux, PSL_n+1(q), L_n+1(q), PSL(n+1,q)
Simplicité: A₁(2) et A₁(3) sont résolubles, les autres sont simples.
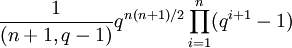
Ordre: ${1\over (n+1,q-1)}q^{n(n+1)/2}\prod_{i=1}^n(q^{i+1}-1)$
Multiplicateur de Schur: Pour les groupes simples, il est cyclique d'ordre (n+1, q − 1), excepté pour A₁(4) (ordre 2), A₁(9) (ordre 6), A₂(2) (ordre 2), A₂(4) (ordre 48, produit de groupes cycliques d'ordres 3, 4, 4), A₃(2) (ordre 2).
Groupe d'automorphisme extérieur: (2, q − 1) ·f·1 pour n = 1 ; (n+1, q − 1) ·f·2 pour n > 1, où q = p^f.
Isomorphismes: A₁(2) est isomorphe au groupe symétrique sur 3 points d'ordre 6. A₁(3) est isomorphe au groupe alterné A₄ (résoluble). A₁(4) et A₁(5) sont isomorphes, et tous deux isomorphes au groupe alterné A₅. A₁(7) et A₂(2) sont isomorphes. A₁(8) est isomorphe au groupe dérivé G₂(3)′. A₁(9) est isomorphe à A₆ et au groupe dérivé B₂(2)'. A₃(2) est isomorphe à A₈.
Remarques: Ces groupes sont obtenus à partir des groupes linéaires généraux GL_n+1(q) en prenant les éléments de déterminant 1 (donnant les groupes linéaires spéciaux SL_n+1(q)) puis après mise en quotient par le centre.

Groupes de Chevalley orthogonaux B_n(q)

n > 1

Simplicité: B₂(2) est non simple et possède un sous-groupe simple d'index 2; les autres sont simples.
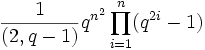
Ordre: ${1\over (2,q-1)} q^{n^2} \prod_{i=1}^n(q^{2i}-1)$
Multiplicateur de Schur: (2,q − 1) excepté pour 'B₂(2) (non simple), B₃(2)

(ordre 2) et B₃(3) (ordre 6).

Groupe d'automorphisme extérieur: (2, q − 1) ·f·1 pour q impair ou n>2; (2, q − 1) ·f·2 si q est pair et n=2, où q = p^f.
Autres noms: $O 2 n + 1 (q)$ , $Ω 2 n + 1 (q)$ (pour q impair).
Isomorphismes: B_n(2^m) est isomorphe à C_n(2^m). B₂(2) est isomorphe au groupe symétrique sur 6 points, et le groupe dérivé B₂(2)' est isomorphe à A₁(9) et à A₆. B₂(3) est isomorphe à ²A₃(2²).
Remarques: Ce groupe est obtenu à partir du groupe orthogonal en dimension 2n+1 en prenant le noyau du déterminant et l'application norme de spin. B₁(q) existe aussi, mais est le même que A₁(q). B₂(q) possède un automorphisme de graphe non-trivial lorsque q est une puissance de 2.

Groupes de Chevalley symplectiques C_n(q)

n > 2

Simplicité: Tous simples.
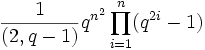
Ordre: ${1\over (2,q-1)} q^{n^2} \prod_{i=1}^n(q^{2i}-1)$
Multiplicateur de Schur: (2,q − 1) excepté pour C₃(2)

(ordre 2).

Groupe d'automorphisme extérieur

(2, q − 1) ·f·1 où q = p^f.

Autres noms: Groupe projectif symplectique, PSp_2n(q), PSp_n(q) (non recommandé), S_2n(q).
Isomorphismes: C_n(2^m) est isomorphe à B_n(2^m).
Remarques: Ce groupe est obtenu à partir du groupe symplectique en 2n dimensions par mise en quotient du centre. C₁(q) existe aussi, mais est le même que A₁(q). C₂(q) existe aussi, mais est le même que B₂(q).

Groupes de Chevalley orthogonaux D_n(q)

n > 3

Simplicité: Tous simples.
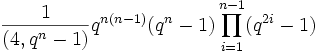
Ordre: ${1\over (4,q^n-1)} q^{n(n-1)} (q^n-1) \prod_{i=1}^{n-1}(q^{2i}-1)$
Multiplicateur de Schur: L'ordre est (4, qⁿ-1) (cyclique pour n impair, abélien élémentaire pour n pair) excepté pour D₄(2) (ordre 4, abélien élémentaire).
Groupe d'automorphisme extérieur

(2, q − 1) ²·f·S₃ pour n=4, (2, q − 1) ²·f·2 pour n>4 pair, (4, qⁿ − 1) ²·f·2 pour n impair, où q = p^f, et S₃ est le groupe symétrique sur 3 points d'ordre 6.

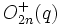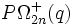Autres noms: $O_{2n}^+(q)$ , $P\Omega_{2n}^+(q)$ .
Remarques: Ce groupe est obtenu à partir de la séparation du groupe orthogonal en dimension 2n en prenant le noyau du déterminant (ou l'invariant de Dickson en caractéristique 2) et l'application norme de spin puis en supprimant le centre.

Les groupes de type D₄ ont un groupe de diagramme d'automorphisme inhabituellement grand d'ordre 6, contenant l'automorphisme de trialité. D₂(q) existe aussi, mais est le même que A₁(q)\times A_1(q). D₃(q) existe aussi, mais est le même que A₃(q).

Groupes de Steinberg unitaires ²A_n(q²)

Autres noms: groupes de Chevalley tordus, groupes spéciaux projectifs unitaires
Notations: ²A_n(q²), PSU_n+1(q), PSU(n+1, q), U_n+1(q), ²A_n(q), ²A_n(q,q²), pour n > 1
Simplicité: ²A₁(q²) et ²A₂(2²) sont résolubles, les autres sont simples.
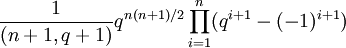
Ordre: ${1\over (n+1,q+1)}q^{n(n+1)/2}\prod_{i=1}^n(q^{i+1}-(-1)^{i+1})$
Multiplicateur de Schur: Cyclique d'ordre (n + 1, q + 1) pour les groupes simples, excepté pour ²A₃(2²) (ordre 2) ²A₃(3²) (ordre 36, produit de groupes cycliques d'ordres 3,3,4), ²A₅(2²) (ordre 12, produit de groupes cycliques d'ordres 2,2,3)
Groupe d'automorphisme extérieur: (n+1, q + 1) · f·1 où q² = p^f.
Isomorphismes: Le groupe résoluble 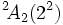${}^2\!A_2(2^2)$ est isomorphe à une extension du groupe de quaternion d'ordre 8 par un groupe abélien élémentaire d'ordre 9. 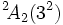${}^2\!A_2(3^2)$ est isomorphe au groupe dérivé G₂(2)'. 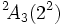${}^2\!A_3(2^2)$ est isomorphe à B₂(3).
Remarques: Ceci est obtenu à partir du groupe unitaire en n+1 dimensions en prenant les sous-groupes d'éléments de déterminant 1 puis par mise en quotient en dehors par le centre.

Groupes de Steinberg orthogonaux ²D_n(q²)

n > 3

Simplicité: Tous simples.
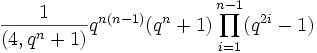
Ordre: ${1\over (4,q^n+1)} q^{n(n-1)} (q^n+1) \prod_{i=1}^{n-1}(q^{2i}-1)$
Multiplicateur de Schur: Cyclique d'ordre (4, qⁿ + 1).
Groupe d'automorphisme extérieur

(4, qⁿ + 1) ·f·1 où $q 2 = p f$ .

Autres noms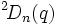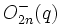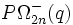: ${}^2\!D_n(q)$ , $O_{2n}^{-}(q)$ , $P \Omega_{2n}^{-}(q)$ , groupe de Chevalley tordu.
Remarques: Ceci est le groupe obtenu à partir du groupe orthogonal non séparé en dimension 2n en prenant le noyau du déterminant (ou l'invariant de Dickson de caractéristique 2) et l'application de norme de spin puis en supprimant le centre.

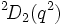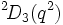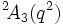${}^2\!D_2(q^2)$ existe aussi, mais est le même que A₁(q). ${}^2\!D_3(q^2)$ existe aussi, mais est le même que ${}^2\!A_3(q^2)$ .

Groupes de type de Lie exceptionnels

Groupes de Chevalley E₆(q)

Simplicité: Tous simples.
Ordre

q³⁶ (q¹²−1) (q⁹−1) (q⁸−1) (q⁶−1) (q⁵−1) (q²−1) /(3,q-1)

Multiplicateur de Schur: (3,q − 1)
Groupe d'automorphisme extérieur

(3, q − 1) ·f·2 où q = p^f.

Autres noms: Groupe de Chevalley exceptionnel.
Remarques: possède deux représentations de dimension 27, et agit sur l'algèbre de Lie de dimension 78.

Groupes de Chevalley E₇(q)

Simplicité: Tous simples.
Ordre

q⁶³ (q¹⁸−1) (q¹⁴−1) (q¹²−1) (q¹⁰−1) (q⁸−1) (q⁶−1) (q²−1) /(2,q-1)

Multiplicateur de Schur: (2,q − 1)
Groupe d'automorphisme extérieur

(2, q − 1) ·f·1 where q = p^f.

Autres noms: Groupe de Chevalley exceptionnel.
Remarques: possède une représentation de dimension 56, et agit sur l'algèbre de Lie correspondante de dimension 133.

Groupes de Chevalley E₈(q)

Simplicité: Tous simples.
Ordre

q¹²⁰ (q³⁰−1) (q²⁴−1) (q²⁰−1) (q¹⁸−1) (q¹⁴−1) (q¹²−1) (q⁸−1) (q²−1)

Multiplicateur de Schur: Trivial.
Groupe d'automorphisme extérieur

1·f·1 où q = p^f.

Autres noms: Groupe de Chevalley exceptionnel.
Remarques: il agit sur l'algèbre de Lie correspondante de dimension 248. E₈(3) contient le groupe simple de Thompson.

Groupes de Chevalley F₄(q)

Simplicité: Tous simples.
Ordre

q²⁴ (q¹²−1) (q⁸−1) (q⁶−1) (q²−1)

Multiplicateur de Schur: Trivial excepté pour F₄(2) (ordre 2).
Groupe d'automorphisme extérieur

1·f·1 pour q impair, 1·f·2 pour q pair, où q = p^f.

Autres noms: Groupe de Chevalley exceptionnel.
Remarques: Ces groupes agissent sur les algèbres de Jordan exceptionnelles à 27 dimensions, qui leur donnent des représentations à 26 dimensions. Ils agissent aussi sur les algèbres de Lie correspondantes de dimension 52. F₄(q) possède un automorphisme de graphe non-trivial lorsque q est une puissance de 2.

Groupes de Chevalley G₂(q)

Simplicité: G₂(2) est non simple mais possède un sous-groupe simple d'index 2; les autres sont simples.
Ordre

q⁶ (q⁶−1) (q²−1)

Multiplicateur de Schur: Trivial pour les groupes simples excepté pour G₂(3) (ordre 3) et G₂(4) (order 2).
Groupe d'automorphisme extérieur

1·f·1 pour q non puissance de 3, 1·f·2 pour q puissance de 3, où q = p^f.

Autres noms: Groupe de Chevalley exceptionnel.
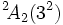Isomorphismes: Le groupe dérivé G₂(2)' est isomorphe à ${}^2\!A_2(3^2)$ .
Remarques: Ces groupes sont des groupes d'automorphismes des algèbres de Cayley de dimension 8 sur des corps finis, qui leur donnes des représentations de dimension 7. Ils agissent aussi sur les algèbres de Lie correspondantes de dimension 14. G₂(q) possède un automorphisme de graphe lorsque q est une puissance de 3.

Groupes de Steinberg ²E₆(q²)

Simplicité: Tous simples.
Ordre

q³⁶ (q¹²−1) (q⁹+1) (q⁸−1) (q⁶−1) (q⁵+1) (q²−1) /(3,q+1)

Multiplicateur de Schur: (3, q + 1) excepté pour 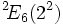${}^2\!E_6(2^2)$ (ordre 12, produit de groupes cyclique d'ordres 2,2,3).
Groupe d'automorphisme extérieur

(3, q + 1) ·f·1 où q² = p^f.

Autres noms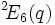: ${}^2\!E_6(q)$ , Groupe de Chevalley tordu.
Remarques: Une des doubles couvertures exceptionnelle de 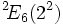${}^2\!E_6(2^2)$ est un sous-groupe du groupe Bébé Monstre,

et l'extension centrale exceptionnelle par le groupe abélien élémentaire d'ordre 4 est un sous-groupe du groupe Monstre.

Groupes de Steinberg ³D₄(q³)

Simplicité: Tous simples.
Ordre

q¹² (q⁸+q⁴+1) (q⁶−1) (q²−1)

Multiplicateur de Schur: Trivial.
Groupe d'automorphisme extérieur

1·f·1 où q³ = p^f.

Autres noms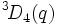: ${}^3\!D_4(q)$ , Groupes de Chevalley tordus.
Remarques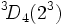: ${}^3\!D_4(2^3)$ agit sur l'unique réseau pair à 26 dimensions de déterminant 3 sans racine.

Groupes de Suzuki ²B₂(2²ⁿ⁺¹) les

Simplicité: Simple pour n>1. Le groupe

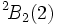${}^2\!B_2(2)$ est résoluble.

Ordre

q² (q²+1) (q−1) où q = 2²ⁿ⁺¹.

Multiplicateur de Schur: Trivial pour n>2, abélien élémentaire d'ordre 4 pour ${}^2\!B_2(8)$ .
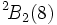Groupe d'automorphisme extérieur

1·f·1 où f = 2n+1.

Autres noms: $S u z (2 2 n + 1)$ , $S z (2 2 n + 1)$ .
Isomorphismes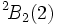: ${}^2\!B_2(2)$ est le groupe de Frobenius d'ordre 20.
Remarques: Les groupes de Suzuki sont des groupes de Zassenhaus agissant sur les ensembles de taille (2²ⁿ⁺¹)²+1, et ont des représentations de dimension 4 sur le corps avec $2 2 n + 1$ éléments. Ce sont les seuls groupes simples non cycliques dont l'ordre n'est pas divisible par 3. Ils ne sont pas reliés au groupe de Suzuki sporadique.

Groupes de Ree ²F₄(2²ⁿ⁺¹) et groupe de Tits

Simplicité: Simple pour n>1. Le groupe dérivé 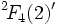${}^2\!F_4(2)'$ est simple d'index 2

dans 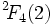${}^2\!F_4(2)$ , il est appelé le groupe de Tits, en l'honneur du mathématicien français Jacques Tits.

Ordre

q¹² (q⁶+1) (q⁴−1) (q³+1) (q−1) où q = 2^2n+1.

^{Le groupe de Tits est d'ordre 17971200 = 2¹¹ · 3³ · 5² · 13.}

Multiplicateur de Schur: Trivial pour n>1 et pour le groupe de Tits.
Groupe d'automorphisme extérieur

1·f·1 où f = 2n+1. Ordre 2 pour le groupe de Tits.

Remarques: Le groupe de Tits n'est pas à strictement parler un groupe de type Lie, et en particulier, n'est pas le groupe de point d'un groupe algébrique simple connecté avec des valeurs dans un certain corps, n'a pas non plus une paire BN. Néanmoins, la plupart des auteurs le comptent comme une sorte de groupe de type Lie honoraire.

Groupes de Ree ²G₂(3²ⁿ⁺¹)

Simplicité: Simple pour n>1. Le groupe 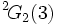${}^2\!G_2(3)$ est non simple, mais son groupe dérivé 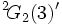${}^2\!G_2(3)'$ est un sous-groupe simple d'index 3.
Ordre

q³ (q³+1) (q−1) où q = 3²ⁿ⁺¹

Multiplicateur de Schur: Trivial pour n>1.
Groupe d'automorphisme extérieur

1·f·1 où f = 2n+1.

Autres noms: $R e e (3 2 n + 1)$ , $R (3 2 n + 1)$ .
Isomorphismes: Le groupe dérivé 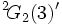${}^2\!G_2(3)'$ est isomorphe à A₁(8).
Remarques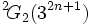: ${}^2\!G_2(3^{2n+1})$ possède une représentation de permutation doublement transitive sur $3 3(2 n + 1) + 1$ points et agit sur un espace vectoriel à 7 dimensions sur le corps avec $3 2 n + 1$ éléments.

Groupes sporadiques

Article principal : Groupe sporadique.

Groupes de Mathieu

Article principal : Groupe de Mathieu.

Groupe de Mathieu M₁₁

Ordre: 2⁴ · 3² · 5 · 11=7 920
Multiplicateur de Schur: Trivial.
Groupe d'automorphisme extérieur: Trivial.
Remarques: Un groupe de permutation 4-transitif sur 11 points, et le point stabilisateur dans $M 12$ . Le sous-groupe fixant un point est quelquefois appelé $M 10$ , et possède un sous-groupe d'index 2 isomorphe au groupe alterné A₆.

Groupe de Mathieu M₁₂

Ordre: 2⁶ · 3³ · 5 · 11 = 95 040
Multiplicateur de Schur: Ordre 2.
Groupe d'automorphisme extérieur: Ordre 2.
Remarques: Un groupe de permutation 5-transitif sur 12 points.

Groupe de Mathieu M₂₂

Ordre: 2⁷ · 3² · 5 · 7 · 11 = 443 520
Multiplicateur de Schur: Cyclique d'ordre 12. Il y a eu plusieurs erreurs dans les calculs initiaux du multiplicateur de Schur, ainsi certains livres et articles anciens listent des valeurs incorrectes.
Groupe d'automorphisme extérieur: Ordre 2.
Remarques: Un groupe de permutation 3-transitif sur 22 points.

Groupe de Mathieu M₂₃

Ordre: 2⁷ · 3² · 5 · 7 · 11 · 23 = 10 200 960
Multiplicateur de Schur: Trivial.
Groupe d'automorphisme extérieur: Trivial.
Remarques: Un groupe de permutation 4-transitif sur 23 points, contenu dans $M 24$ .

Groupe de Mathieu M₂₄

Ordre: 2¹⁰ · 3³ · 5 · 7 · 11 · 23 = 244823040
Multiplicateur de Schur: Trivial.
Groupe d'automorphisme extérieur: Trivial.
Remarques: Un groupe de permutation 5-transitif sur 24 points.

Groupes du réseau de Leech

Article principal : Réseau de Leech.

Groupe de Janko J₂

Article principal : Groupe de Janko.

Ordre: 2⁷ · 3³ · 5² · 7 = 604 800
Multiplicateur de Schur: Ordre 2.
Groupe d'automorphisme extérieur: Ordre 2.
Autres noms: Groupe de Hall-Janko, HJ
Remarques

C'est le groupe d'automorphisme d'un graphe de rang 3 sur 100 points, et est aussi contenu dans G₂(4).

Groupe de Conway Co₁

Article principal : Groupes de Conway.

Ordre: 2²¹ · 3⁹ · 5⁴ · 7² · 11 · 13 · 23 = 4 157 776 806 543 360 000
Multiplicateur de Schur: Ordre 2.
Groupe d'automorphisme extérieur: Trivial.
Autres noms: ·1
Remarques: La double couverture parfaite de Co₁ est le groupe d'automorphisme du réseau de Leech, et est quelquefois noté par ·0.

Groupe de Conway Co₂

Article principal : Groupes de Conway.

Ordre: 2¹⁸ · 3⁶ · 5³ · 7 · 11 · 23 = 42 305 421 312 000
Multiplicateur de Schur: Trivial.
Groupe d'automorphisme extérieur: Trivial.
Autres noms: ·2
Remarques: Sous-groupe de Co₁ qui fixe un vecteur de la norme 4 dans le réseau de Leech.

Groupe de Conway Co₃

Article principal : Groupes de Conway.

Ordre: 2¹⁰ · 3⁷ · 5³ · 7 · 11 · 23 = 495 766 656 000
Multiplicateur de Schur: Trivial.
Groupe d'automorphisme extérieur: Trivial.
Autres noms: ·3
Remarques: Sous-groupe de Co₁ qui fixe un vecteur de la norme 6 dans le réseau de Leech.

Groupe de Higman-Sims HS

Article principal : Groupe de Higman-Sims.

Ordre: 2⁹ · 3² · 5³· 7 · 11 = 44 352 000
Multiplicateur de Schur: Ordre 2.
Groupe d'automorphisme extérieur: Ordre 2.
Remarques: Il agit comme un groupe de permutation de rang 3 sur le graphe de Higman Sims avec 100 points et est contenu dans le Co₃.

Groupe de McLaughlin McL

Article principal : Groupe de McLaughlin.

Ordre: 2⁷ · 3⁶ · 5³· 7 · 11 = 898 128 000
Multiplicateur de Schur: Ordre 3.
Groupe d'automorphisme extérieur: Ordre 2.
Remarques: Il agit comme un groupe de permutation de rang 3 sur le graphe de McLauglin avec 275 points et est contenue dans Co₃.

Groupe de Suzuki sporadique Suz

Article principal : Groupe de Suzuki.

Ordre: 2¹³ · 3⁷ · 5²· 7 · 11 · 13 = 448 345 497 600
Multiplicateur de Schur: Ordre 6.
Groupe d'automorphisme extérieur: Ordre 2.
Autres noms: $S z$
Remarques: Le revêtement à 6 variétés agit sur un réseau à 12 dimensions sur les entiers d'Eisenstein. Il n'est pas relié aux groupes de Suzuki de type de Lie.

Sous-groupes du Monstre

Groupe de Fischer Fi₂₂

Article principal : Groupe de Fischer.

Ordre: 2¹⁷ · 3⁹ · 5² · 7 · 11 · 13 = 64 561 751 654 400
Multiplicateur de Schur: Ordre 6.
Groupe d'automorphisme extérieur: Ordre 2.
Autres noms: $M (22)$
Remarques: Un groupe 3-transposition dont la double couverture est contenue dans $F i 23$ .

Groupe de Fischer Fi₂₃

Article principal : Groupe de Fischer.

Ordre: 2¹⁸ · 3¹³ · 5² · 7 · 11 · 13 · 17 · 23 = 4 089 470 473 293 004 800
Multiplicateur de Schur: Trivial.
Groupe d'automorphisme extérieur: Trivial.
Autres noms: $M (23)$
Remarques: Un groupe 3-transposition contenue dans $F i 24$ .

Groupe de Fischer Fi₂₄′

Article principal : Groupe de Fischer.

Ordre: 2²¹ · 3¹⁶ · 5² · 7³ · 11 · 13 · 17 · 23 · 29 = 1 255 205 709 190 661 721 292 800
Multiplicateur de Schur: Ordre 3.
Groupe d'automorphisme extérieur: Ordre 2.
Autres noms: $M (24)'$ , $F i 24'$ .
Remarques: La triple couverture est contenue dans le groupe Monstre.

Groupe de Held He

Article principal : Groupe de Held.

Ordre: 2¹⁰ · 3³ · 5²· 7³· 17 = 4 030 387 200
Multiplicateur de Schur: Trivial.
Groupe d'automorphisme extérieur: Ordre 2.
Autres noms: Groupe de Held-Higman-McKay, HHM, F₇.
Remarques: Il centralise un élément d'ordre 7 dans le groupe Monstre.

Groupe de Harada-Norton HN

Article principal : Groupe de Harada-Norton.

Ordre: 2¹⁴ · 3⁶ · 5⁶ · 7 · 11 · 19 = 273 030 912 000 000
Multiplicateur de Schur: Trivial.
Groupe d'automorphisme extérieur: Ordre 2.
Autres noms: F₅, $D$
Remarques: Il centralise un élément d'ordre 5 dans le groupe Monstre.

Groupe de Thompson fini Th

Article principal : Groupe de Thompson.

Ordre: 2¹⁵ · 3¹⁰ · 5³ · 7² · 13 · 19 · 31 = 90745943887872000
Multiplicateur de Schur: Trivial.
Groupe d'automorphisme extérieur: Trivial.
Autres noms: F₃, $E$
Remarques: Il centralise un élément d'ordre 3 dans le Monstre et est contenu dans E₈(3).

Groupe Bébé Monstre B

Article détaillé : Groupe Bébé Monstre.

Ordre: 2⁴¹ · 3¹³ · 5⁶ · 7² · 11 · 13 · 17 · 19 · 23 · 31 · 47 = 4 154 781 481 226 426 191 177 580 544 000 000
Multiplicateur de Schur: Ordre 2.
Groupe d'automorphisme extérieur: Trivial.
Autres noms: F₂
Remarques: Le double revêtement du groupe Bébé Monstre est contenu dans le groupe Monstre.

Groupe Monstre M

Articles détaillés : Groupe Monstre et Conjecture Monstrous Moonshine.

Notations: M, F₁, M₁
Autres noms: Groupe de Fischer-Griess, monstre de Fischer, Géant amical.
Ordre: 2⁴⁶ · 3²⁰ · 5⁹ · 7⁶ · 11² · 13³ · 17 · 19 · 23 · 29 · 31 · 41 · 47 · 59 · 71 = 808 017 424 794 512 875 886 459 904 961 710 757 005 754 368 000 000 000
Multiplicateur de Schur: Trivial.
Groupe d'automorphisme extérieur: Trivial.
Remarques: Le groupe Monstre est le groupe d'automorphisme de l'algèbre de Griess à 196884 dimensions et de l'algèbre vertex monstre, il agit naturellement sur l'algèbre de Lie Monstre. Il contient quasiment tous les autres groupes sporadiques, à part 6 groupes sporadiques que l'on nomme parias. Il est relié à la conjecture Monstrous Moonshine.

Parias

Groupe de Janko J₁

Article principal : Groupe de Janko.

Ordre: 2³ · 3 · 5 · 7 · 11 · 19 = 175 560
Multiplicateur de Schur: Trivial.
Groupe d'automorphisme extérieur: Trivial.
Autres noms: $J (1)$ , $J (11)$
Remarques: C'est un sous-groupe de G₂(11), et donc possède une représentation à 7 dimensions sur le corps à 11 éléments.

Groupe de Janko J₃

Article principal : Groupe de Janko.

Ordre: 2⁷ · 3⁵ · 5 · 17 · 19 = 50 232 960
Multiplicateur de Schur: Ordre 3.
Groupe d'automorphisme extérieur: Ordre 2.
Autres noms: Groupe de Higman-Janko-McKay, HJM
Remarques: J₃ semble ne pas être relié à un quelconque groupe sporadique (ou à quoi que ce soit d'autre). Sa triple couverture possède une représentation à 9 dimensions sur le corps à 4 éléments.

Groupe de Janko J₄

Article principal : Groupe de Janko.

Ordre: 2²¹ · 3³ · 5 · 7 · 11³ · 23 · 29 · 31 · 37 · 43 = 86 775 571 046 077 562 880
Multiplicateur de Schur: Trivial.
Groupe d'automorphisme extérieur: Trivial.
Remarques: possède une représentation à 112 dimensions sur le corps à 2 éléments.

Groupe de O'Nan O'N

Article principal : Groupe de O'Nan.

Notation: O'N, O'NS
Autres noms: Groupe de O'Nan-Sims
Ordre: 2⁹ · 3⁴ · 5 · 7³ · 11 · 19 · 31 = 460 815 505 920
Multiplicateur de Schur: Ordre 3.
Groupe d'automorphisme extérieur: Ordre 2.
Remarques: Le triple revêtement possède deux représentations à 45 dimensions sur le corps à 7 éléments, échangé par un automorphisme extérieur.

Groupe de Rudvalis Ru

Article principal : Groupe de Rudvalis.

Ordre: 2¹⁴ · 3³ · 5³· 7 · 13 · 29 = 145 926 144 000
Multiplicateur de Schur: Ordre 2.
Groupe d'automorphisme extérieur: Trivial.
Remarques: Le double revêtement agit sur un réseau à 28 dimensions sur les entiers de Gauss.

Groupe de Lyons Ly

Article principal : Groupe de Lyons.

Notations: Ly, LyS.
Autres noms: Groupe de Lyons-Sims.
Ordre: 2⁸ · 3⁷ · 5⁶ · 7 · 11 · 31 · 37 · 67 = 51 765 179 004 000 000
Multiplicateur de Schur: Trivial.
Groupe d'automorphisme extérieur: Trivial.
Remarques: Possède une représentation à 111 dimensions sur Z/5Z, le corps des congruences modulo 5.

Liste par ordre croissant

La liste suivant recense les groupes simples finis non-cycliques d'ordre inférieur à 10 000. Les groupes cycliques ne sont pas inclus dans cette liste dans la mesure où tout groupe cyclique d'ordre p est simple dès que p est premier, ce qui est le cas pour 1 229 nombres inférieurs à 10 000.

Groupe	Ordre (valeur)	Ordre (factorisation)
A₅ = A₁(4) = A₁(5)	60	2² · 3 · 5
A₁(7) = A₂(2)	168	2³ · 3 · 7
A₆ = A₁(9) = B₂(2)′	360	2³ · 3² · 5
A₁(8) = ²G₂(3)′	504	2³ · 3² · 7
A₁(11)	660	2² · 3 · 5 · 11
A₁(13)	1 092	2² · 3 · 7 · 13
A₁(17)	2 448	2⁴ · 3² · 17
A₇	2 520	2³ · 3² · 5 · 7
A₁(19)	3 420	2² · 3² · 5 · 19
A₁(16)	4 080	2⁴ · 3 · 5 · 17
A₂(3)	5 616	2⁴ · 3³ · 13
²A₂(9)	6 048	2⁵ · 3³ · 7
A₁(23)	6 072	2³ · 3 · 11 · 23
A₁(25)	7 800	2³ · 3 · 5² · 13
M₁₁	7 920	2⁴ · 3² · 5 · 11
A₁(27)	9 828	2² · 3³ · 7 · 13

Voir aussi

Liens internes

Liens externes

(en) D. Madore, « Orders of non abelian simple groups », 22 janvier 2003. Consulté le 6 septembre 2008
(en) J. N. Bray, R. A. Parker & R. A. Wilson, « Atlas of Finite Group Representations ». Consulté le 6 septembre 2008

Bibliographie

Daniel Gorenstein, Richard Lyons, Ronald Solomon The Classification of the Finite Simple Groups (volume 1), AMS, 1994 (volume 2), AMS,
Conway, J. H.; Curtis, R. T.; Norton, S. P.; Parker, R. A.; and Wilson, R. A.: "Atlas of Finite Groups: Maximal Subgroups and Ordinary Characters for Simple Groups." Oxford, England 1985.
Simple Groups of Lie Type by Roger W. Carter, ISBN 0-471-50683-4

Portail des mathématiques

Ce document provient de « Liste des groupes finis simples ».

Catégories : Groupe fini | Groupe remarquable

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Liste Des Groupes Finis Simples de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Liste des groupes finis simples — En mathématiques, la classification des groupes finis simples établit que chacun de ces groupes est soit un cyclique, soit alterné, soit membre d une des seize familles de groupes de type de Lie (incluant le groupe de Tits), soit l un des 26… … Wikipédia en Français
Groupes finis simples — Liste des groupes finis simples En mathématiques, la classification des groupes finis simples établit que chacun de ces groupes est soit un cyclique, soit alterné, soit membre d une des seize familles de groupes de type de Lie (incluant le groupe … Wikipédia en Français
GROUPES (mathématiques) - Groupes finis — Née de l’étude des groupes de permutations des racines d’équations, la théorie des groupes finis s’est développée indépendamment depuis le Traité des substitutions et des équations algébriques (1870) de Camille Jordan. Après les travaux… … Encyclopédie Universelle
Groupes finis — Groupe fini En mathématiques, un groupe fini est un groupe constitué d un nombre fini d éléments, c est à dire que son cardinal est fini. Sommaire 1 Introduction 2 Parité de l ordre et involution 3 Exemples … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Liste des petits groupes — La liste mathématique suivante contient tous les groupes finis d ordre inférieur ou égal à 17, à isomorphisme près. Sommaire 1 Terminologie et notations 2 Petits groupes abéliens 3 Petits groupes non abéliens … Wikipédia en Français
Catégorie des groupes — Groupe (mathématiques) Pour les articles homonymes, voir Groupe. Cet article concerne une introduction au concept de groupe. Pour un approfondissement, voir théorie des groupes … Wikipédia en Français
Théorie des Groupes — Groupe (mathématiques) Pour les articles homonymes, voir Groupe. Cet article concerne une introduction au concept de groupe. Pour un approfondissement, voir théorie des groupes … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Classification des groupes simples finis — La classification des groupes finis simples, aussi appelée le théorème énorme, est un vaste corps de travail en mathématiques, principalement publié entre environ 1955 et 1983, qui a pour but de classer tous les groupes simples finis. En tout, le … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Liste Des Groupes Finis Simples