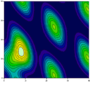
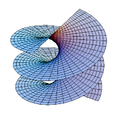
Fonction de deux variables

Articles d'analyse vectorielle
Objets d'étude
Champ vectoriel	Champ scalaire
Équation aux dérivées partielles
de Laplace	de Poisson
Opérateurs
Nabla	Gradient
Rotationnel	Divergence
Laplacien scalaire	Bilaplacien
Laplacien vectoriel	D'alembertien
Théorèmes
de Green	de Stokes
de Helmholtz	de flux-divergence
du gradient	du rotationnel

En mathématiques, une fonction de plusieurs variables f est la donnée d'un ensemble de départ E (un espace topologique à n dimensions), d'un ensemble d'arrivée F et d'une relation associant à chaque n-uplet x = (x₁,x₂,...,x_n) d'éléments de l'ensemble de départ un et un seul élément de l'ensemble d'arrivée, que l'on appelle image de x par f et que l'on note f(x) ou f(x₁,...,x_n) :

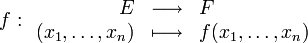
Plus formellement encore, une telle fonction est définie comme le triplet

où G, ensemble appelé graphe de f, est une partie du produit cartésien E × F telle que pour tout élément x de E il existe un et un seul élément y de F tel que le couple (x,y) appartienne à G.

Catégorisation

Objet	Représentation	Application	Opérations particulières
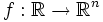
Courbe			Calcul de longueur d'un arc, de courbure.
Surface	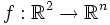		Calcul de superficie, de courbure.
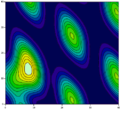
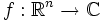
Champ scalaire			Calcul d'extremum, de gradient, de dérivée directionnelle, d'intégrale multiple, d'intégrale de surface, d'intégrale curviligne, de flux.
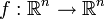
Champ vectoriel			Calcul de gradient, de divergence, de rotationnel, d'intégrale de surface, d'intégrale curviligne, de flux.

Analyse à plusieurs variables

Les concepts classiques de l'analyse s'étendent aux fonctions de plusieurs variables. L'introduction de l'algèbre linéaire se montre indispensable.

Limites et continuité

soit f une fonction définie sur D telle que f est une application ; f est continue si lim f(x,y)=f(a,b) lorsque (x,y) tend vers (a,b)

Calcul différentiel

Les dérivées partielles généralisent le concept de dérivée. Une dérivée partielle d'une fonction de plusieurs variables est la dérivée de cette fonction selon une variable, les autres étant considérées constantes.

Les dérivées partielles peuvent être combinées en de nombreuses façons pour créer des objets différentiels intéressants. En analyse vectorielle, l'opérateur nabla est utilisé pour définir des opérateurs comme le gradient, la divergence et le rotationnel. Une matrice des dérivées partielles premières, la matrice jacobienne, peut être utilisée pour représenter la dérivée d'une fonction d'un nombre quelconque de variables. La matrice hessienne est son analogue avec des dérivées partielles secondes.

Les équations différentielles contenant des dérivées partielles sont appelées équations aux dérivées partielles ou équations différentielles partielles (EDP). Elles sont généralement plus difficiles à résoudre que les équations différentielles ordinaires.

Calcul intégral

L'intégrale multiple généralise le concept d'intégrale. Les intégrales doubles et triples peuvent être utilisées pour calculer des surfaces et des volumes de régions de l'espace. Leur calcul passe généralement par leur expression en une composition d'intégrales simples, calculées à chaque fois selon une seule variable.

L'intégrale de surface et l'intégrale curviligne sont utilisées pour l'intégration sur des variétés.

Théorèmes fondamentaux de l'analyse à plusieurs variables

En analyse, ces théorèmes établissent un lien entre la dérivée et l'intégrale. Le lien entre dérivées partielles et intégrales multiples est assuré par les théorèmes du gradient, de flux-divergence, du rotationnel, de Green.

Dans une étude plus avancée de l'analyse vectorielle, on constate que ces théorèmes ne sont que l'incarnation d'un théorème plus général, le théorème de Stokes, qui s'applique à l'intégration de formes différentielles sur des variétés.

Analyse vectorielle

L'analyse vectorielle étudie les champs de scalaires et de vecteurs suffisamment réguliers des espaces euclidiens, c'est-à-dire les applications différentiables d'un ouvert d'un espace euclidien E à valeurs respectivement dans ℝ et dans E. L'analyse vectorielle est donc une branche – outre de l'analyse à plusieurs variables – de la géométrie différentielle.

Mais l'importance de l'analyse vectorielle provient de son utilisation intensive en physique et dans les sciences de l'ingénieur. C'est pourquoi nous nous limitons le plus souvent au cas où E = ℝ³ est l'espace usuel à trois dimensions. Dans ce cadre, un champ de vecteurs associe à chaque point de l'espace un vecteur (à trois composantes réelles), tandis qu'un champ de scalaires y associe un réel. Imaginons par exemple l'eau d'un lac. La donnée de sa température en chaque point forme un champ de scalaires, celle de sa vitesse en chaque point, un champ de vecteurs. L'analyse vectorielle est ainsi un outil fondamental de la mécanique des fluides, de la météorologie, de l'électrostatique, de l'électrodynamique, de la géophysique, etc.

Voir aussi

• application (mathématiques)
• analyse vectorielle
• géométrie différentielle

• Portail des mathématiques