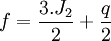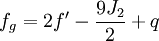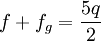Figure de la Terre : le sphéroïde de Clairaut

Sphéroïde de Clairaut

Alexis Clairaut (1713–1765), élu membre de l'Académie Royale des Sciences de Paris à seize ans. C'est à lui qu'on doit l'ouvrage capital sur la figure de la Terre. Dans ce livre, paru en 1743, Clairaut (on écrivait aussi Clairaux et Clairault) posa les fondations de l'hydrostatique moderne, dont la formulation actuelle fut donnée par Leonhard Euler (1707–1783) quelques années plus tard.

Page de titre de la première édition (1743) du célèbre ouvrage de Clairaut

Dans son célèbre ouvrage « Théorie de la Figure de la Terre, Tirée des Principes de l'Hydrostatique » publié en 1743, Alexis Claude Clairaut (1713–1765) fit une synthèse des rapports existant entre la pesanteur et la forme de la Terre. Membre de la mission en Laponie, ce mathématicien hors-pair avait aussi une solide expérience de terrain. Dans le préambule de son livre, il examine la théorie des tourbillons de Descartes pour conclure qu'elle ne convient pas au problème, qui selon lui doit être traité dans l'esprit de la théorie de Newton en tenant compte des lois de l'hydrostatique établies par Pascal et d'autres. Il écrit en particulier : «… Les lois de l'hydrostatique ne pourraient-elles pas permettre que cette masse d'eau eût une forme irrégulière, qu'elle fût aplatie par un pôle, allongée de l'autre et que les méridiens ne fussent pas semblables ? En ce cas les opérations faites en Laponie, en France et au Pérou ne pourraient nous donner la vraie figure de la Terre. On sait par les premiers principes de cette science qu'un fluide ne saurait être en repos à moins que la surface ne soit de niveau c'est-à-dire perpendiculaire à la ligne à plomb, parce qu'alors chaque goutte n'a plus de pente à couler d'un côté que de l'autre. De là il suit que si la force avec laquelle tous les corps tombent étant toujours dirigée vers un même centre, la Terre devrait être parfaitement ronde… mais si au contraire la pesanteur suit une ligne qui ne passe pas par le centre, la Terre ne sera plus sphérique, mais elle aura la forme nécessaire pour qu'en chacun des points de la surface elle soit coupée perpendiculairement par la direction de la pesanteur en ce point. Toute la question de la forme de la Terre est donc fondée sur la loi selon laquelle la force de pesanteur agit… ».

La théorie de la forme hydrostatique fut formulée par Clairaut au milieu du XVIII^e siècle, puis étendue dans les décennies et siècles suivants par d'éminents savants comme Legendre, Laplace, Roche, Lyapunov et Poincaré, et d'autres à peine moins distingués. En fait, le problème de la forme de la Terre a constitué l'un des problèmes majeurs de la science du XIX^e siècle siècle. Il fut à l'origine de très importants progrès en mathématiques et en mécanique, ainsi qu'en astronomie et en géodésie, et il est toujours à l'ordre du jour.

Théorème de Clairaut

Sphéroïde de Clairaut

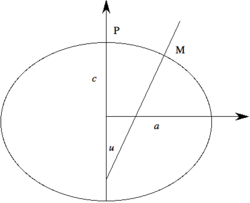
Parmi les résultats essentiels obtenus par Clairaut, citons les suivants : Soit un corps de révolution symétrique par rapport à l'équateur, de rayon équatorial a et de rayon polaire c, et supposons que l'aplatissement géométrique défini par le rapport 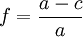, est petit. Dénotons par u l'angle que fait la verticale en un point quelconque M de la surface avec l'axe des pôles. L'équation de cette surface, appelée sphéroïde de Clairaut, est r = a(1 − f.cos²u) en première approximation.

Soient γ_e et γ_p les pesanteurs à l'équateur et aux pôles, et 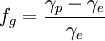l' aplatissement gravimétrique. Clairaut a montré que, dans ces circonstances, la pesanteur sur le sphéroïde sera de la forme γ(M) = γ_e(1 + f_g.cos²u).

Comme l'angle u est la colatitude du point M, on se rend compte que Clairaut retrouve ainsi par la théorie le résultat que Maupertuis avait déduit d'une douzaine d'expériences pendulaires à différentes latitudes. Cette dernière équation, munie d'un terme supplémentaire très petit pour tenir compte des effets du second ordre, constitue à l'heure actuelle la formule internationale de la pesanteur. Tous les gravimétristes l'utilisent pour réduire leurs observations.

D'autre part, si ω désigne la vitesse angulaire de rotation du corps de masse M et de moments d'inertie A et C par rapport aux axes équatorial et polaire, respectivement, on définit alors le facteur de forme dynamique par 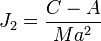et la constante géodynamique q par le rapport de l'accélération centrifuge à l'accélération de la pesanteur à l'équateur, c'est-à-dire .

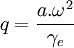Clairaut a montré qu'entre les quatre nombres f, f_g, J₂ et q, il existe les trois relations suivantes:

La première de ces trois relations algébriques constitue le théorème de Clairaut. Elle possède une signification profonde, en ce sens qu'elle associe dans une même expression la quantité géométrique f, la quantité cinétique J₂ et la quantité dynamique q. La dernière relation est tirée des deux premières en éliminant J₂. En effet, Clairaut admet seulement que la surface du corps est de niveau constant, au sens du nivellement, celle qu'épouserait une pellicule liquide recouvrant l'entièreté de la surface. La troisième équation ci-dessus ne dépend donc pas d'éventuelles variations de la densité, ni de la structure interne du corps, pourvu que sa surface externe soit de niveau. Comme la valeur de q est bien connue et l'était déjà du temps de Clairaut, à savoir q ≅ 1/288, il suffit de déterminer le paramètre f_g, c'est-à-dire les variations de la pesanteur, pour déduire de la troisième relation l'aplatissement géométrique f. Un calcul aisé permet de vérifier que pour une densité interne constante, on trouve .

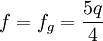Autrement dit, on retrouve la valeur 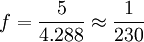annoncée par Newton. D'autre part, pour un corps quasi-sphérique, 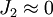. Dans ces conditions, la première des trois relations ci-dessus fournit f ≅ 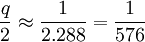, qui est la valeur prévue par Huyghens. Qui plus est, Clairaut tira d'importantes conclusions concernant la constitution de la Terre en admettant que celle-ci, bien que solide, se comporte comme un corps en équilibre hydrostatique. C'est souvent l'hypothèse qu'on fait encore actuellement lorsqu'on étudie la structure interne de la Terre et des planètes. La théorie de Clairaut était en avance d'un siècle et demi par rapport aux possibilités techniques permettant sa pleine application. En effet, ce n'est qu'à la fin du XIX^e siècle ou au début du XX^e siècle que les méthodes géodésiques commençaient à être assez précises pour pouvoir tirer profit de cette théorie. En tout cas, elle justifiait entièrement l'interprétation des observations de Richer et elle permettait même de soupçonner des incompatibilités entre l'aplatissement que l'on pouvait déduire en utilisant la troisième relation et l'aplatissement qu'on pouvait calculer par la géométrie en attribuant au méridien un profil elliptique.

Clairaut conclut en ces termes : «… Mais la comparaison de la théorie avec les observations achèvera peut-être de décider en faveur d'un système qui a déjà tant d'apparence d'être vrai, je veux dire celui de Mr. Newton. Car l'attraction étant supposée, je démontre que, toutes les hypothèses les plus vraisemblables qu'on puisse faire sur la densité des parties internes de la terre, il y a toujours une telle liaison entre la fraction qui exprime la différence des axes et celle qui exprime la diminution de la pesanteur du pôle à l'équateur que si l'une de ces deux fractions surpasse 1/230, l'autre doit être moindre et précisément de la même quantité ; or, comme toutes les expériences que l'on a faites sur la longueur du pendule nous montrent que la diminution de la pesanteur du Pôle à l'équateur est plus grande que 1/230, on doit conclure que la différence des axes est moindre ».

En fait, les mesures pendulaires de l'époque auraient pu fournir, grâce à la troisième relation de Clairaut, des estimations de f comprises entre 1/274 et 1/303, donc assez voisines de la valeur moderne fournie par la géodésie spatiale, il n'en allait pas de même pour les mesures d'arcs de méridien. En effet, on montre que le rayon de courbure d'une ellipse méridienne dont l'aplatissement est faible est donné en bonne approximation par 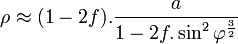, où φ est la latitude et a le demi-grand axe de l'ellipse. Si nous désignons par ρ₁ et ρ₂ deux rayons de courbure se rapportant respectivement aux latitudes 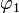et 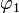(φ₂) des points moyens de deux mesures d'arc, on trouve 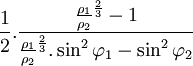. Or, 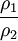est précisément égal au rapport des arcs de 1° mesurés par triangulation. La méridienne de Laponie avait fourni 57438 toises par degré à une latitude moyenne de 66°20', celle de France 57074 toises par degré à une latitude moyenne de 49°29' et celle du Pérou 56746 toises par degré à une latitude moyenne de 1°30' S. Notons encore la valeur amendée par Le Monnier pour l'arc Paris-Amiens de 57183 (au lieu de 57074) toises par degré à la même latitude moyenne de 49°29' que celle retenue par La Caille.

Les valeurs de f déduites de mesures d'arcs en France, en Laponie, en Equateur et au Cap de Bonne-Espérance se répartissent entre les valeurs extrêmes 1/125 et 1/1271, qui n'ont guère de signification physique. Les raisons de cette dispersion des valeurs de l'aplatissement terrestre obtenues par triangulation donnaient lieu à des discussions fort animées qui se sont poursuivies pendant très longtemps. Il s'est avéré qu'une partie de l'erreur provenait d'un désaccord d'environ 10^–3 entre la toise de Picard et celle de l'Académie. Une erreur plus importante — dont on ne s'est rendu compte que bien plus tard — s'était glissée dans les mesures astronomiques de Maupertuis en Laponie.

Comme on le voit, la période qui s'étend entre 1650 et 1750 fut marquée par des progrès inestimables, tant du point de vue expérimental et observationnel que du point de vue théorique. Elle vit la naissance et l'acceptation définitive — entre 1720 et 1740 — de la théorie de la gravitation de Newton pour expliquer le mouvement des corps célestes et la forme de la Terre et des planètes. Pendant cette époque, la géodésie et l'astronomie géodésique connurent un essor sans précédent. Celui-ci fut au départ à peu près exclusivement à mettre au compte de savants français qui, sous l'égide de l'Académie Royale des Sciences de Paris, organisaient de grandes campagnes astrogéodésiques et gravimétriques à travers le monde, dans le but de déterminer l'aplatissement de la Terre et de vérifier la théorie de Newton. Bien sûr, la Science ne fut pas l'apanage des seuls Français. Ainsi, l'an 1700 vit la fondation de l'Académie Royale des Sciences de Prusse à Berlin, et l'an 1725, la création de l'Académie Impériale des Sciences de Russie à Saint-Pétersbourg. De même que l'Académie des Sciences de Paris et la Société Royale de Londres, ces institutions vont jouer un rôle très important dans la suite pour faire progresser les connaissances scientifiques. Entretemps, Isaac Newton et Gottfried Wilhelm Leibniz (1646–1716) avaient inventé le calcul différentiel et intégral (calcul des fluxions), lequel fut développé notamment par Jacques Bernoulli (1654–1705) et son frère Jean Bernoulli (1667–1748), par le marquis Guillaume de L'Hospital (1661–1704), par James Gregory (1638–1675) et par bien d'autres.

Sphéroïde de Maclaurin

Colin Maclaurin (1698–1746). Portrait réalisé par le 11^e Comte de Buchan, d'après un portrait plus ancien peint par James Ferguson.

En 1728, l'année de la découverte de l'aberration de la lumière par Bradley, Newton montre, à partir de sa loi de la gravitation, qu'une montagne doit avoir une action sur le fil à plomb, et il en calcule la valeur dans un cas particulier en supposant que la densité moyenne de la Terre est de l'ordre de 5 à 6 fois celle de l'eau. Ce calcul incitera Bouguer à faire des observations au fil à plomb lors de la mission au Pérou, dans le but de déterminer la densité moyenne, et donc la masse, de la Terre. En 1742, le savant écossais Colin Maclaurin, lauréat de l'Académie Royale des Sciences de Paris en 1740 pour un essai sur les marées, démontre qu'un ellipsoïde de révolution aplati peut être une figure d'équilibre pour une masse fluide pesante homogène en rotation. On démontrera plus tard que ce sphéroïde de Maclaurin, aux propriétés géométriques bien définies en fonction de la densité et de la vitesse de rotation, est la seule figure d'équilibre stable sous les hypothèses données, lorsque le rapport de la force centrifuge à l'équateur à la force de gravité ne dépasse pas un seuil critique. Ce problème est aussi étudié à la même époque par Thomas Simpson (1710–1761), un mathématicien qui a aussi laissé une formule très utilisée pour effectuer des quadratures numériques.

Triomphe de la théorie de gravitation de Newton : prévision du passage de la comète de Halley

Même les plus grands sceptiques durent être convaincus de la validité de la théorie de la gravitation de Newton lors du passage en 1758 d'une comète dont le retour pour cette année-là avait été prévu par Sir Edmund Halley en fondant ses calculs sur la théorie de la gravitation universelle. Halley fit sa prévision en 1705, après de longs calculs qui utilisaient ses observations de l'orbite de la comète apparue en 1682.^[1]

D'autre part, le pape Benoît XIV, connu pour avoir annulé la condamnation de Galilée, fit entreprendre par Roger Joseph Boscovich (1711–1787) en 1751 une chaîne de triangulation dans les États Pontificaux, de Rome à Rimini. C'est à cette époque que les recherches en physique et en mathématiques se multiplient partout en Europe et apportent leur contributions aux idées et connaissances caractérisant le « Siècle des Lumières ». On assiste alors à la naissance de la physique mathématique, sous l'impulsion de savants comme de Leonhard Euler (1707–1783), Daniel Bernoulli (1700–1782), le fils de Jean Bernoulli, Colin Maclaurin (1698–1746), Alexis Clairaut (1713–1765), Jean Le Rond d'Alembert (1717–1783), le comte Louis Lagrange (1736–1813), et bien d'autres esprits éclairés. Beaucoup de travaux de physique mathématique de l'époque trouvaient leur origine dans des questions posées par la géodésie et l'astronomie, à côté bien sûr de problèmes de physique « pure », par exemple le problème des cordes vibrantes étudié par D'Alembert, des questions d'hydrodynamique et de théorie cinétique envisagées par Daniel Bernoulli, ou encore de mécanique traitées par exemple par Euler et Lagrange. D'Alembert s'occupe aussi à cette époque de l'équilibre d'une masse fluide en rotation, un problème directement en rapport avec le problème de la forme de la Terre.

Constante de précession

Après la publication par Bradley, en 1747, de son importante découverte de la nutation de l'axe des pôles, D'Alembert en fit la théorie dans son ouvrage intitulé Recherches sur la précession des équinoxes et sur la nutation de l'axe de la Terre dans le système newtonien paru en 1749. Il y montrait que ces mouvements de précession-nutation dépendent du rapport

H = (C–A)/C,

où C et A sont les moments d'inertie par rapport à l'axe polaire et par rapport à un axe situé dans le plan de l'équateur, respectivement, le corps étant supposé de révolution autour de l'axe polaire. La constante de précession (ou aplatissement dynamique) H est déterminée par des observations astronomiques. Elle joue un rôle fondamental dans beaucoup de problèmes de géodynamique et de géodésie physique. Sa valeur est 1/305, à peu de chose près. Or, on peut montrer que pour un modèle homogène, l'aplatissement dynamique H serait égal à l'aplatissement géométrique f. Il en résultait que la Terre n'était pas un sphéroïde homogène, auquel la théorie aurait imposé l'aplatissement f = 1/230 calculé par Newton.^[2] Cette dernière valeur, préconisée par Euler sur la base de critères fort subjectifs pour la Terre réelle, devait dès lors être rejetée.

Équation différentielle de Clairaut

Par contre, il était possible de concilier les valeurs observées de H, de f (déduite des mesures au pendule par la troisième relation de Clairaut fournie plus haut) et une valeur théorique de f en supposant que la densité à l'intérieur de la Terre croît avec la profondeur et en déterminant l'aplatissement théorique en intégrant une équation différentielle aussi fournie par Clairaut dans son ouvrage sur la figure de la Terre. Avec des notations modernes, l'équation différentielle de Clairaut peut s'écrire comme suit :

d²f/ds² + (6 Δ/s) df/ds + [6 (Δ – 1)/s²] f = 0,

où la variable indépendante s est le rayon de la sphère qui possède le même volume que celui contenu à l'intérieur d'une surface équipotentielle quelconque repérée justement par s. L'aplatissement de cette strate équipotentielle interne est f = f(s) et sa densité est ρ = ρ(s). La densité moyenne de la matière contenue dans ce volume est D = D(s). Sous ces conditions, la fonction Δ = Δ(s) représente le rapport ρ/D, qui est un nombre pur. La variable s, communément appelée le rayon moyen, varie de s=0 (le centre) à s=R (la surface extérieure). L'équation différentielle précédente doit être intégrée en imposant qu'au centre l'aplatissement f(s) prenne une valeur finie f(0) et qu'à la surface on ait la relation

[df/ds + 2 f/s]_s=R = (5/2) q/R.

Cette dernière condition aux limites résulte de la théorie de Clairaut. Pour que l'on puisse effectuer cette intégration, il faut connaître la fonction Δ(s), et donc la densité ρ(s), à chaque niveau, puisque la densité moyenne D(s) se déduit de ρ(s) par une intégration.

L'équation différentielle de Clairaut relie l'aplatissement à la loi de densité en fonction du rayon moyen ou, ce qui revient au même, en fonction de la profondeur. Au départ, on ne connaissait pas, même de manière approchée, la distribution des masses à l'intérieur de la Terre. On en était donc réduit à des hypothèses plus ou moins plausibles. Dans cette alternative, plutôt que de servir d'équation permettant de calculer l'aplatissement théorique pour un modèle de densité connu, on se servait de cette équation pour valider un modèle de densité hypothétique. On cherchait ainsi un modèle de densité qui soit compatible, via l'équation différentielle de Clairaut, avec une valeur observée de l'aplatissement à laquelle on accordait un certain crédit. Le modèle devait en outre posséder les valeurs réelles du rayon moyen et de la masse de la Terre. Il s'agit-là typiquement de la résolution d'un problème géodésique ou géophysique inverse, consistant à inférer des propriétés concernant l'intérieur de la Terre au moyen de données mesurées en surface ou à l'extérieur.^[3]

Bibliographie

Clairaut, A.C. (1743). Théorie de la Figure de la Terre, Tirée de l'Hydrostatique. Chez David Fils, Paris ; deuxième édition parue en 1808 chez Courcier, Paris.

Dugas, R. (1950). Histoire de la Mécanique, Éditions du Griffon, Neuchâtel & Éditions Dunod, Paris.

Lacombe, H. & P. Costabel, éditeurs (1988). La figure de la Terre du XVIII^e siècle à l'ère spatiale, Académie des Sciences et Gauthier-Villars, Paris.

Levallois, J.-J. (1988). Mesurer la Terre (300 ans de géodésie française — De la toise du Châtelet au satellite), Association Française de Topographie — Presses de l'École Nationale des Ponts et Chaussées.

Loridan, Abbé J. (1890). Voyages des Astronomes français à la recherche de la figure de la terre et de ses dimensions, Desclée, de Brouwer et Cie, Lille.

Taton, R. (1994). Histoire générale des sciences (4 volumes), Quadrige/Presses Universitaires de France, Paris.

Ouvrage technique en anglais :

Todhunter, I. (1873). A History of the Mathematical Theories of Attraction and the Figure of the Earth (2 volumes), Macmillan & Co, London ; facsimilé publié en 1962 par Dover Editions Inc, New York.

Notes

Liens internes

Voici quelques liens vers des articles ayant trait à l'histoire de la géodésie et de la Figure de la Terre :

• Figure de la Terre dans l'Antiquité,
• Figure de la Terre au Moyen Âge,
• Figure de la Terre à la Renaissance,
• Figure de la Terre et gravitation universelle,
• Modèle ellipsoïdal de la Terre,
• Figure de la Terre et les expéditions de Laponie et du Pérou,
• Sphéroïde de Clairaut,
• Masse de la Terre,
• Figure de la Terre et méridienne de Delambre et Méchain,
• Figure de la Terre et histoire du mètre,
• De l'ellipsoïde au géoïde.
• Géoïde

Liens externes

• Chronologie de la vie de Clairaut (1713-1765)

• Portail de la géodésie et de la géophysique
• Portail de la physique
• Portail de l’astronomie
• Portail de la géographie