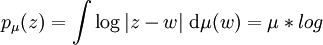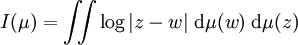Theorie du potentiel

Sommaire 1 Fonction potentielle 2 Capacité 3 Voir aussi 4 Bibliographie

Fonction potentielle

La théorie du potentiel est une branche des mathématiques qui s'est développée à partir de la notion physique de potentiel newtonien introduite par Poisson pour les besoins de la mécanique newtonienne.

Elle concerne l'étude de l'opérateur laplacien et notamment des fonctions harmoniques et sous harmoniques. Dans le plan complexe par exemple, cette théorie commence par l'étude de la fonction potentiel et de son énergie définies de la manière suivante:

Soit μ une mesure de Borel finie à support compact dans . Le potentiel associé est défini sur par

L'énergie I(μ) de μ est définie comme étant la somme des potentiels:

Le potentiel est un exemple simple de fonction sous harmonique. Un théorème de représentation de Riesz nous dit que sous certaines conditions très simples, les fonctions sous harmoniques sont les fonctions potentielles, modulo l'ensemble des fonctions harmoniques. Cette remarque donne donc tout son intéret à l'étude des fonctions potentielles.

Capacité

La capacité est une fonction agissant sur les ensembles. Elle est à la théorie du potentiel, ce que la mesure est à la théorie de la mesure. Elle permet en quelque sorte de mesurer la taille d'un ensemble, au sens de la théorie du potentiel. Elle apparait naturellement dans plusieurs domaines des mathématiques, notamment en théorie de l'approximation ou en analyse complexe.

Si E est un sous ensemble de , sa capacité est définie comme étant 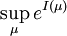, le sup étant pris sur toutes les mesures de probabilité de Borel.

On peut modifier légèrement la définition du potentiel, en remplaçant la distance euclidienne d(z,w) = | z − w | par la pseudo-distance hyperbolique, dans le cas où E est un sous ensemble du disque unité, ou par la distance sphérique, dans le cas où E est un sous ensemble de la sphère de Riemann. Cela fournira alors de nouvelles capacités, respectivement la capacité hyperbolique et la capacité sphérique ou elliptique de E.

Un ensemble E est dit polaire s'il est de capacité nulle. On peut montrer qu'un sous ensemble du disque unité est polaire si et seulement s'il est polaire relativement aux capacités hyperbolique et elliptique.

Un ensemble polaire est nécessairement de mesure de Lebesgue nulle. Les ensembles polaires et F_σ sont totalement discontinus. On peut voir que la réciproque à ces deux assertions est fausse. L'ensemble triadique de Cantor est totalement discontinu et de mesure nulle, mais n'est pas de capacité nulle.

La capacité est relativement difficile à manipuler et à étudier, du fait qu'elle n'est ni additive, ni sous ou sur additive.

Voir aussi

• Opérateur laplacien
• Équation de Laplace
• Équation de Poisson
• Fonction de Green
• Paul-André Meyer
• Théorème de Tsuji

Bibliographie

• Paul Appell, Lecons sur l'attraction et la fonction potentielle, professées a la Sorbonne en 1890-1891, Georges Carré, Paris, 1892. Disponible en ligne : Cornell Library Historical Mathematics Monographs.
• Henri Poincaré, Théorie du potentiel Newtonien - Leçons professées à la Sorbonne pendant le premier semestre 1894-1895, Gauthiers-Villars, Paris, 1899. Disponible en ligne : Cornell Library Historical Mathematics Monographs.

• B.O. Pierce, Elements of the theory of the Newtonian potential function, Ginn & Co., Boston, 1902. Disponible en ligne : Cornell Library Historical Mathematics Monographs.

• Thomas Ransford Potential theory in modern function theory, Cambridge university press

• Portail des mathématiques
• Portail de la physique