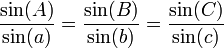- Abul Wáfa
-
Abu l-Wafa
Abu l-Wafa ou Abu l-Wāfā’ ou Muhammad Aboûl-Wafâ, (en persan : محمد ابوالوفای بوزجانی), né en 940 à Bouzjan et mort en 998 à Bagdad était un astronome et mathématicien persan principalement connu pour ses apports en trigonométrie plane et en trigonométrie sphérique.
Sommaire
Biographie
Né en 939 ou 940 à Buzjan dans la région de Khorosan, d'une grande famille de Taif, il étudie les mathématiques auprès de ses oncles.
En 959, il émigre à Bagdad où il restera jusqu'à sa mort pendant l'apogée de la dynastie abbasside. Sous le règne des Bouyides, `Adhud ad-Dawla et son fils Charaf ad-Dawla, Bagdad devient un important centre culturel. Introduit à la cour, Abu l-Wafa rejoint al-Quhi et al-Sijzi comme astronome.
Parallèlement à ses observations astronomiques, Abu l-Wafa s'intéresse à la géométrie, la trigonométrie, l'algèbre et correspond avec les autres scientifiques de son époque
Contributions
Astronomie
Abu l-Wafa s'intéresse aux mouvements de la lune. Il observe en particulier, à Bagdad, l'éclipse de lune du 24 mai 997 concomitamment avec al-Biruni situé à Kath, permettant ainsi de préciser la différence de longitude entre les deux villes. Il corrige les tables lunaires de son époque mettant en évidence ce que Tycho Brahe appellera la troisième variation.
Trigonométrie
Dans son livre La révision de l'Almageste (en allusion à l'Almageste de Ptolémée), il corrige et complète les tables trigonométriques de ses prédécesseurs notamment sur la tangente. On lui doit la notion de cercle trigonométrique, celles de sécante et cosécante. On lui attribue aussi la formule des sinus en trigonométrie sphérique
Géométrie
Abu l-Wafa commente les œuvres d'Euclide, Diophante et al-Khwarizmi (ces commentaires ont disparu). Dans son livre Sur l'indispensable aux artisans en fait de construction, il développe des constructions approchées à la règle et au compas de polygones réguliers à cinq, sept ou neuf côtés. Il s'intéresse en particulier aux constructions réalisables avec un compas d'écartement constant. Il propose une construction de la parabole. Il propose des constructions mécaniques de trisections d'angles et de duplication du cube. Il s'intéresse au problème de la division d'un carré en somme de plusieurs carrés.
Il est connu pour une solution par construction géométrique du problème suivant. Soit ABCD un carré de centre O avec un point quelconque E sur le segment BC et F le point symétrique à E par rapport à la droite (AC). La question est : le triangle AEF peut-il être équilatéral ?
Pour résoudre ce problème, il faut d'abord prouver que F est sur le segment CD. La solution proposée par Abu l-Wafa est la suivante :
- Construire le cercle circonscrit à ABCD.
- Construire un second cercle, de centre C et passant par O.
- Dénoter les deux points auxquels ces cercles se coupent en U et V.
- On peut alors prouver que les droites (AU) et (AV) coupent le carré en deux points qui sont les points E et F recherchés.
Arithmétique
Dans son livre Ce qui est nécessaire en arithmétique pour les comptables et les hommes d'affaires, il développe des mathématiques en même temps théoriques (fraction, multiplication, division, mesures) et pratiques (calculs de taxes, unités de monnaies, paiement de traitements). Bien que connaissant la numération indienne, il ne l'utilise pas dans cet ouvrage adressé au grand public. Il développe cependant une théorie sur les nombres négatifs les associant à l'image d'un dette : 3 - 5 représentant par exemple une dette de 2. Il accepte de multiplier ces nombres négatifs par des positifs et de les incorporer dans des calculs.
Optique
Abu l-Wafa s'intéresse aussi à l'optique et publie un livre sur les miroirs ardents, miroirs dont tous les rayons réfléchis convergent en un même point, permettant ainsi d'obtenir en ce point une chaleur suffisante pour enflammer un objet.
Écrits
Abu l-Wafa a écrit de nombreux livres dont certains ont disparu :
- Kitab fi ma yahtaj ilayh al-kuttab wa'l-ummal min 'ilm al-hisab (Ce qui est nécessaire en arithmétique pour les comptables et les hommes d'affaires) entre 961 et 976 ;
- Kitab al-Handasa (Sur l'indispensable aux artisans en fait de construction) ;
- Al-Kitab al-Kamil (Le livre complet), une révision de l'Almageste ;
- une théorie sur la Lune (disparu) ;
- El Wadih (des tables trigonométriques, disparu) ;
- un traité sur les coniques (disparu) ;
- Kitab al-maraya al-muhriqa (Livre sur les miroirs ardents).
Voir aussi
Sources
- Hebri Bousserouel, Les savants musulmans oubliés de l'histoire.
- Ahmed Djebbar, Une histoire de la science arabe.
- (en) John J. O'Connor et Edmund F. Robertson, Abu l-Wafa, MacTutor History of Mathematics archive.
- Biographie sur le site d'Imago Mundi
- Portail de l’astronomie
- Portail des mathématiques
- Portail de l’Iran
- Portail du monde arabo-musulman
Catégories : Mathématicien de Perse | Astronome | Astronome de Perse | Scientifique arabo-musulman | Naissance en 940 | Décès en 998
Wikimedia Foundation. 2010.