Cissoïde de Dioclès

Cissoïde de Dioclès
Cissoïde de Dioclès avec son cercle et sa droite génératrice

La cissoïde de Dioclès est une courbe construite par Dioclès au IIe siècle av. J.‑C. dans le but de résoudre graphiquement le problème de la duplication du cube. Elle fut étudiée plus complètement au XVIIe siècle par Fermat, Huygens et Sluse.

Le terme cissoïde vient du grec (kissos, lierre) et signifie en forme de lierre. Il est emprunté à Proclus qui en parle comme d'une courbe présentant des points de rebroussement[1]


Sommaire

Fiche signalétique

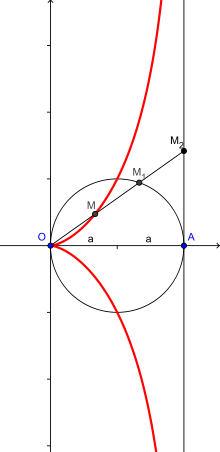
La cissoïde de Dioclès fait partie de la famille des cissoïdes. Elle est appelée aussi cissoïde droite car elle est engendrée par un cercle C et une droite (d) tangente au cercle en A. Si O est le point diamétralement opposé à A sur le cercle, la cissoïde est l'ensemble des points M tels que

\overrightarrow{OM} = \overrightarrow{M_1M_2}

où M1 et M2 sont deux points alignés avec O situés respectivement sur (C) et (d).

Cette courbe possède l'axe (OA) comme axe de symétrie et la droite (d) comme asymptote

Il en existe plusieurs équations[2]. On appelle a le rayon du cercle (C), et on se place dans un repère orthonormal direct \scriptstyle (O,\vec i, \vec j), dans lequel A a pour coordonnées (2a,0).

  • Son équation polaire est
r(\theta) =2a\dfrac{\sin^2(\theta)}{\cos(\theta)}
où θ parcourt l'intervalle ]-π/2;π/2[
  • Son équation cartésienne est
y^2=\dfrac{x^3}{2a-x}
  • Son équation paramétrée par t = tan(θ) est
x=2a\dfrac{t^2}{1+t^2}
y=tx\,

L'aire comprise entre la courbe et son asymptote est finie et vaut 3πa²


Histoire

Cissoïde Version Dioclès

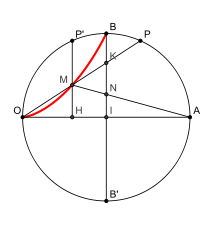
Dans un ouvrage aujourd'hui disparu Sur les miroirs ardents, Diocles construit cette courbe point par point pour obtenir un outil permettant de dupliquer le cube. On dit que la cissoïde de Diocles est une duplicatrice. Diocles ne construit qu'une demi-portion de la cissoïde située dans le cercle et s'en sert pour construire un cube dont le volume doit être dans un rapport k avec celui d'un cube donné[3]. Il ne se sert pas de la tangente pour sa construction. Il construit deux diamètres perpendiculaires [OA] et [BB']. Pour tout point P de l'arc BA, il construit le symétrique P' de P par rapport à la droite (BB'). Le point d'intersection M entre la droite (OP) et la perpendiculaire à (OA) passant par P' est un point de la cissoïde. Si H est le projeté orthogonal de P' sur (OA), K le point d'intersection des droites (OP) et (BB') et I le centre du cercle, Dioclès démontre, en utilisant le théorème de Thalès et des propriétés sur les triangles semblables que

\frac{IK}{IO}=\frac{MH}{OH}=\frac{OH}{HP'}=\frac{HP'}{HA}

par produit, il en déduit que

\left(\frac{IK}{IO}\right)^3 = \frac{MH}{HA}

enfin si N est le point d'intersection de (AM) et (BB')

\left(\frac{IK}{IO}\right)^3 = \dfrac{IN}{IA}

Pour connaitre le côté d'un cube dont le volume serait k fois le volume du carré de côté a (k<1), il suffit alors de construire une cissoïde à partir du cercle de rayon a. de construire sur (BB') le point N tel que IN=k×IA. La droite (AN) rencontre la cissoïde en M et la droite (OM) rencontre alors (BB') en K vérifiant

\dfrac{IK^3}{IO^3}=k

En prenant par exemple k=1/2, on construit deux cubes dont les volumes sont dans un rapport 2. Dioclès fait ensuite remarquer que par le jeu des proportionnalités, la construction peut s'effectuer grâce à la cissoïde associée au cercle de rayon 1.

Dioclès montre ensuite que cette même figure permet de résoudre le problème de la double moyenne proportionnelle : a et b étant donné, comment trouver x et y tels que

\frac ax=\frac xy = \frac yb

Sa méthode a probablement inspiré Sporus et est reprise par Eutocius quand celui-ci fait l'inventaire des duplicatrices[3].

Selon Jean Itard[4] , à cette époque, le nom de cissoïde de Dioclès n'est pas utilisé et le terme semble apparaître pour la première fois dans des textes du XVIe siècle.

Le verre de Sluse (portion), de volume fini et de contenance infinie

Au XVIIe siècle, la cissoïde est étudiée par Pierre de Fermat dans ses ouvrages Doctrine sur les tangentes[5] et De Cissoide Fragmentum (1662) où il en détermine les tangentes et une quadrature. C'est à cette époque (1658) que la cissoide se prolonge hors du cercle, se complète par symétrie et que son asymptote apparait [6] . Elle fait l'objet d'un échange de lettres entre Sluse, Huygens et Wallis. Utilisant la méthode des indivisibles, Sluse calcule le volume du solide engendré par la rotation de la demi-cissoide autour de son asymptote et prouve qu'il est égal à la moitié celui du solide engendré par la rotation du cercle directeur autour de sa tangente en O[7]. Il trouve ainsi un volume de π²a³. Utilisant la même méthode des indivisibles, Huyghens calcule l'aire comprise entre la cissoïde, le diamètre du cercle et son asymptote et prouve qu'elle est égale à trois fois l'aire du demi-cercle directeur[8], soit 3πa²/2. Peu confiant en cette méthode, il demande à Wallis de confirmer son calcul par sa méthode Arithmética infinotorum, ce que celui-ci fait en 1659[9]. Grâce au théorème de Guldin, en complétant la courbe par symétrie, Huygens trouve la posïtion du centre de gravité G de la surface comprise entre la courbe et son asymptote (AG=1/3 a). Toujours en utilisant le théorème de Guldin, Sluse en déduit le volume du solide obtenu par rotation de la surface comprise entre l'asymptote, le diamètre (OA) et la cissoïde, autour de la tangente au cercle en O. (V=5π²a³). Sluse se réjouit d'avoir ainsi trouvé un solide aussi bizarre que la trompette de Gabriel : un solide de volume fini pouvant contenir un volume infini: il parle alors dans une lettre à Huygens de « meansura vasculi, pondere non magni, quod interim helluo nullus ebibat » - mesure d'un verre, dont le poids n'est pas grand mais que nul ne peut vider.

Constructions

Construction mécanique

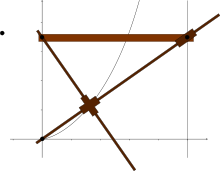
Dispositif mécanique d'Artobolevski

La cissoïde est une courbe algébrique car son équation est polynomiale de degré 3. D'après Kempe[10], on peut donc lui associer un système traceur mécanique. Artobolevski en propose[11] une version.

Inversion

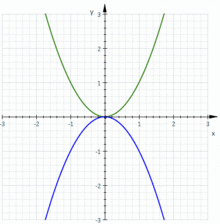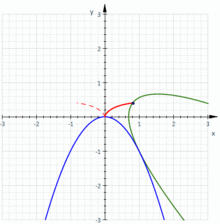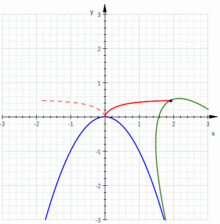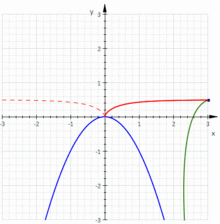
La cissode est l'image de la parabole d'équation x = y² par l'inversion de pole O et de rapport 2a

Podaire

La cissoïde est la podaire d'une parabole par rapport à son sommet

Roulette

Construction de la cissoïde par roulement sur une parabole

La cissoïde est une sorte de roulette obtenue en faisant rouler une parabole sur une parabole qui lui soit symétrique et en observant le lieu de son sommet.


Notes et références

  1. ↑ Paul Tannery, Charles Henry, Oeuvres de Fermat, ed Gauthiers -Villars, 1891, Oeuvres de Fermat - Livre Ip159, note 3
  2. ↑ Les formules sont vérifiables par exemples sur le site de Robert Ferreol, Cissoïde de Dioclès ou Cissoïde droite avec un paramétrage différent pour a.
  3. ↑ a et b Wilbur Richard Knorr, Textual studies in ancient and medieval geometry,pp 81-87
  4. ↑ Jean Itard,Revue des sciences et de leurs applications, année 1956 volume 9, numéro 9-4, p 368
  5. ↑ Ce fascicule sans titre se présente comme un complément sur la méthode des maxima et minima (voir s:Page:Fermat - Livre 1-000207.jpg
  6. ↑ Hans Niels Jahnke, A history of analysis, p 58.
  7. ↑ Hans Niels Jahnke, A history of analysis, p 63.
  8. ↑ Hans Niels Jahnke, A history of analysis, p 63.
  9. ↑ Hans Niels Jahnke, A history of analysis, p 66.
  10. ↑ Alain Juhel, Au-delà du compas : 3000 ans de dépassement, Voyage au pays des mathématiques
  11. ↑ APMEP, Duplication du cube, trisection de l'angle, quadrature du cercle : rien d'impossible

Bibliographie

  • Hans Niels Jahnke, A history of analysis;
  • Wilbur Richard Knorr, Textual studies in ancient and medieval geometry.

Voir aussi

Liens internes

Liens externes

v · courbes
Coniques (cercle, ellipse, parabole, hyperbole)
Cardioïde • Cissoïde • Clothoïde • Conchoïde • Cycloïde • Épicycloïde • Folium de Descartes • Hélice
Hypocycloïde (astroïde, deltoïde) • Hypotrochoïde • Néphroïde • Spirale (d'Archimède, logarithmique) • Strophoïde
Lemniscates (lemniscate de Gerono, lemniscate de Booth, lemniscate de Bernoulli, courbe du diable)
Trajectoire • Ovale de Cassini • Chaînette • Courbe brachistochrone

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Cissoïde de Dioclès de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Cissoide — Cissoïde La cissoïde ou (courbe) cissoïdale de deux courbes (C1) et (C2) par rapport à un point fixe O est le lieu géométrique des points P tels que : où P1 est un point de (C1) et P2 un point de (C2), P1 et P2 étant alignés avec O. La… …   Wikipédia en Français

  • Diocles (mathematicien) — Dioclès (mathématicien) Pour les articles homonymes, voir Dioclès. Dioclès était un mathématicien et géomètre grec, qui vécut vers la fin du IIe siècle av. J. C. et au début du Ier siècle av. J. C …   Wikipédia en Français

  • Dioclès (Mathématicien) — Pour les articles homonymes, voir Dioclès. Dioclès était un mathématicien et géomètre grec, qui vécut vers la fin du IIe siècle av. J. C. et au début du Ier siècle av. J. C …   Wikipédia en Français

  • Dioclès le mathématicien — Dioclès (mathématicien) Pour les articles homonymes, voir Dioclès. Dioclès était un mathématicien et géomètre grec, qui vécut vers la fin du IIe siècle av. J. C. et au début du Ier siècle av. J. C …   Wikipédia en Français

  • Cissoïde — La cissoïde ou (courbe) cissoïdale de deux courbes (C1) et (C2) par rapport à un point fixe O est le lieu géométrique des points P tels que : où P1 est un point de (C1) et P2 un point de (C2), P1 et P2 étant alignés avec O. La cissoïde peut… …   Wikipédia en Français

  • Dioclès (mathématicien) — Pour les articles homonymes, voir Dioclès. Dioclès (vers 240 vers 180) était un mathématicien et géomètre grec, qui vécut vers la fin du IIIe siècle av. J.‑C. et au début du IIe siècle av. J.‑C.. Il est probablement le premier …   Wikipédia en Français

  • Cissoid of Diocles — construction In geometry, the cissoid of Diocles is a cubic plane curve notable for the property that it can be used to construct two mean proportionals to a given ratio. In particular, it can be used to double a cube. It can be defined as the… …   Wikipedia

  • Cisoide de Diocles — (línea roja). El segmento OA es igual a OC menos OB. La cisoide de Diocles es la cisoide generada por el vector posición de una recta paralela al eje OY (Curva 1), que pasa por el punto (2a,0), al que se le resta el radio vector de una… …   Wikipedia Español

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”