Parité de zéro

Zéro objets, divisés en deux groupes égaux.

Zéro est un nombre pair, étant donné qu'il remplit la définition d'un nombre pair : être un multiple de deux. Par conséquent, zéro partage toutes les propriétés qui découlent de cette définition : comme tous les autres nombres pairs, 0 est divisible par 2, 0 est précédé et suivi par des nombres impairs, 0 est la somme d'un entier avec lui-même, et zéro objets peuvent être divisés entre deux groupes égaux. Zéro respecte les lois de somme et de produit de nombres pairs, comme par exemple pair - pair = pair, de sorte que toute autre définition^{[Laquelle ?]} des nombres pairs se doit de considérer zéro comme un nombre pair.^{[interprétation personnelle]} Dans l'ensemble des nombres pairs, zéro joue un rôle central : c'est l'élément neutre du groupe des entiers pairs et c'est le premier élément de la définition par récurrence des nombres pairs.^{[réf. nécessaire]} Tout entier divise 0, dont toutes les puissances de deux ; en ce sens, 0 est le nombre le « plus pair » de tous.

D'un point de vue psychologique, la parité de 0 est moins bien comprise que celle de 2 ou 3. Il a été observé que la plupart des gens mettaient plus de temps à identifier 0 comme un nombre pair que les autres nombres pairs. Les écoliers tout comme les professeurs de l'enseignement primaire pensent parfois à tort que la parité de zéro est ambigüe, ou même que zéro est impair.^{[réf. nécessaire]} Plusieurs chercheurs en enseignement des mathématiques ont écrit que de telles fausses idées répandues constituaient des opportunités pour la recherche^{[citation nécessaire]}. Certaines propositions comme 0 × 2 = 0 peuvent révéler les craintes des élèves à considérer 0 comme un nombre et à l'utiliser en arithmétique. Parler de la parité de zéro en classe peut déclencher de violents débats, les étudiants se confrontant aux principes de base du raisonnement mathématique, comme l'importance de définitions précises. Alors que la compréhension de zéro est déjà un objectif louable pour un écolier, l'évaluation de sa parité peut constituer une première introduction à une idée omniprésente en mathématiques : l'abstraction d'une idée familière pour aller vers quelque chose de moins familier et de parfois inattendu.

Pourquoi zéro est-il pair ?

Il est facile de prouver directement que zéro est pair :

• Un nombre est pair si c'est un multiple entier de 2. Zéro est un multiple entier de 2, car 0 × 2 = 0, donc 0 est pair^[1].

Cette preuve utilise la définition précise de ce qu'est un « nombre pair », mais on peut aussi expliquer le fait que zéro est pair sans une telle définition^[2]. Les explications qui vont suivre justifient ce fait sur des idées plus fondamentales. On peut d'ailleurs ensuite en conclure la définition elle-même ainsi que son applicabilité à zéro.

Explications basiques

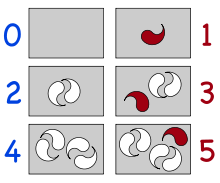La boîte avec 0 objets n'a pas d'objet rouge laissé tout seul^[3].

Une utilisation basique des nombres est le comptage. Étant donné un ensemble d'éléments, on fait appel à un certain nombre pour décrire combien il y a d'éléments dans l'ensemble. Zéro correspond au compte d'un ensemble où il n'y aurait pas d'éléments ; plus formellement, c'est le nombre d'éléments de l'ensemble vide. L'idée de parité est utilisée lorsqu'on fait des sous-groupes de deux éléments. Si les éléments de l'ensemble peuvent être divisés en groupes de deux, sans qu'aucun élément ne reste tout seul, alors le nombre total d'éléments est pair. Si un élément reste tout seul, le nombre d'éléments est impair^[4].

L'ensemble vide contient zéro groupes de deux, aucun objet n'étant laissé tout seul, donc zéro est pair. Bien qu'il soit difficile de s'imaginer zéro groupes de deux, ou de porter attention à l'inexistence d'un élément seul, cette conception de la parité de zéro peut être illustrée en comparant l'ensemble vide avec d'autres ensembles, comme sur le diagramme à droite^[4].

La droite des nombres fournit une autre méthode de description des nombres pairs, que ce soit parmi les nombres positifs, négatifs ou zéro. La répartition des nombres pairs et impairs apparaît clairement lorsqu'on distingue ceux-ci visuellement :

Les nombres pairs et impairs sont alternés. En partant d'un nombre pair quelconque et en allant ensuite à deux rangs à droite ou à gauche du nombre choisi, on obtient un autre nombre pair ; il n'y a alors aucune raison de sauter le nombre zéro^[5].

La parité peut être approchée de manière plus formelle en utilisant l'arithmétique. Tout entier est soit de la forme (2 × ▢) + 0, soit de la forme (2 × ▢) + 1; ; la première forme représentant les nombres pairs et la seconde les nombres impairs. Par exemple, 1 est impair car 1 = (2 × 0) + 1 et 0 est pair car 0 = (2 × 0) + 0.

Définition de la parité

La définition précise de toute notion mathématique comme « pair », défini par « multiple entier de deux » est, dans l'absolu, une convention. Contrairement à « pair », certains termes mathématiques^[6] sont définis de manière à exclure les cas dégénérés et triviaux.

Il est donc théoriquement possible de redéfinir le mot « pair » de façon à ce que zéro ne soit plus un nombre pair.^{[réf. nécessaire]} Cependant, cela rendrait plus difficile l'énoncé de théorèmes concernant les nombres pairs, dont les propriétés arithmétiques des nombres pairs et impairs^[7].

Histoire

Il est difficile d'établir quand, dans l'histoire des mathématiques, la première personne s'est intéressée à la parité de zéro, et il y a peu de documents à ce sujet. Ce qui est certain est que l'idée de nombres pairs et impairs a été introduite avant celle du zéro.^{[réf. nécessaire]} Cette évolution historique est en fait calquée sur le développement progressif des concepts mathématiques chez les enfants^[8]. Les propriétés algébriques de 0, comme par exemple 0 × n = 0, ont été étudiées de façon systématique pour la première fois par les mathématiciens indiens, comme Brahmagupta au VII^e siècle,^{[réf. nécessaire]} ce qui est arrivé assez tard par rapport à l'histoire de la théorie des nombres.^{[réf. nécessaire]}

Les mathématiciens de la Grèce antique considéraient généralement 2 comme le premier nombre pair et 3 comme le premier nombre impair, certains allant même jusqu'à estimer que 2 n'est pas un nombre pair^[9]. Le nombre 1 n'était pas considéré comme un vrai nombre, mais une composante de tous les autres nombres ; en tant que tel, il devait donc être à la fois pair et impair, et donc ni vraiment pair ni vraiment impair. Ce rôle double que jouait le nombre 1 a été source de problèmes métaphysiques ; un historien a affirmé que les Grecs auraient pu éviter ce problème s'ils avaient eu plus de connaissances sur le nombre 0^[10].

Notes et références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Parity of zero » (voir la liste des auteurs), dont les sources étaient :

Sources citées

• (en) Deborah Loewenberg Ball, Jennifer Lewis et Mark Hoover Thames, Making mathematics work in school, vol. M14, 2008 [lire en ligne (page consultée le 4 March 2010)], p. 13–44 and 195–200 
• (en) W. K. C. Guthrie, A History of Greek Philosophy: The Earlier Presocratics and the Pythagoreans, Cambridge, Cambridge UP, 1992 (ISBN 0521294207) 
• (en) Esther Levenson, Pessia Tsamir et Dina Tirosh, Neither even nor odd: Sixth grade students’ dilemmas regarding the parity of zero, vol. 26, 2007, p. 83–95 
• (en) Betty Plunkett Lichtenberg, « Zero is an even number », dans The Arithmetic Teacher, vol. 19, n^o 7, novembre 1972, p. 535–538 
• (en) Barbara Hall Partee, Fundamentals of Mathematics for Linguistics, Dordrecht, D. Reidel, 1978 (ISBN 90-277-0809-6) 
• (en) Robert C. Penner, Discrete Mathematics: Proof Techniques and Mathematical Structures, River Edje, World Scientific, 1999 (ISBN 981-02-4088-0) 
• (en) Platon et Reginald E. Allen, Plato's Parmenides, Yale University Press, 1997 (ISBN 0300077297) 

Voir aussi

Article connexe

Pont aux ânes

Bibliographie

• Portail des mathématiques