Base de Hilbert

Base de Hilbert
David Hilbert en 1912

Une base de Hilbert (du nom de David Hilbert), ou encore base hilbertienne, est une généralisation aux espaces de Hilbert de la notion classique de base orthonormée en algèbre linéaire, pour les espaces euclidiens (ou hermitiens dans le cas complexe), lesquels sont de dimension finie.

Comme dans le cas des bases habituelles, il s'agit de pouvoir décomposer n'importe quel vecteur de l'espace en somme de vecteurs colinéaires à ceux de la famille choisie. Cependant dans le cas d'une base de Hilbert, on ne peut pas (généralement) écrire une égalité entre le vecteur décomposé et une combinaison linéaire finie des vecteurs de la base : on doit généralement se contenter d'une série dont les termes sont colinéaires aux vecteurs de la base, et convergeant vers le vecteur à décomposer (la notion de convergence d'une série a ici un sens car un espace de Hilbert est en particulier un espace vectoriel normé).

Sommaire

Définition

Soit H un espace préhilbertien sur un corps K égal aux nombres réels ou complexes et {}^{F=(e_i)_{i\in I}} une famille de vecteurs de H.

Définition —  On dit que F est une base de Hilbert de H si et seulement si :

\forall (i,j)\in I^2\quad i\ne j \Rightarrow \langle e_i \mid e_j\rangle = 0
\forall i\in I\quad \langle e_i \mid e_i\rangle = \Vert e_i \Vert^2 = 1

(ce qui entraîne : {}^{\sum_{i\in I}\lambda_i\cdot e_i=\sum_{i\in I}\mu_i\cdot e_i\Rightarrow\forall i\in I,~\lambda_i=\mu_i})

  • la famille est de plus complète au sens suivant :
\forall x\in H,\ \exists (\lambda_i)_{i\in I}\quad\text{tel que}\quad \sum_{i\in I} \lambda_i\cdot e_i = x

La sommabilité de la famille (\lambda_i\cdot e_i )_{i \in I} (de somme x) est celle associée à la norme du produit scalaire de H.

Dans le cas où H est de dimension finie, cette définition coïncide avec celle de base orthonormale. Dans le cas d'un espace de dimension infinie, le terme de base orthonormale indique très généralement une base de Hilbert[1].

Approche intuitive

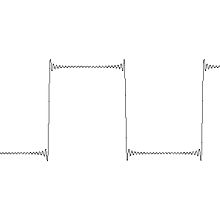
Décomposition d'une fonction créneau sur la base de Hilbert des polynômes trigonométriques. Seuls les dix premiers vecteurs de la base sont utilisés, proposant ainsi une approximation.
Avec 50 termes, la décomposition de la fonction créneau sur la base de Hilbert devient plus précise.

Depuis le XVIIIe siècle, les mathématiciens ont tenté de résoudre certaines questions à l'aide de séries de fonctions. Leonhard Euler étudie le problème de la détermination de la somme des inverses des carrés d'entiers[2]. Une série de polynômes trigonométriques permet de résoudre cette épineuse question ouverte depuis presque un siècle[3]. Joseph Fourier utilise une approche similaire pour étudier l'équation de la chaleur[4].

Le XXe siècle voit une formalisation à la fois moderne générale et géométrique de l'approche. David Hilbert considère les fonctions utilisées comme des éléments d'un espace vectoriel de dimension infinie. Il est équipé du produit scalaire suivant, permettant de bénéficier des techniques de la géométrie euclidienne :

\langle f, g\rangle = \int f(x)g(x) dx

Un espace euclidien dispose de bases orthonormales, une généralisation du théorème de Pythagore permet simplement de calculer les coordonnées d'un vecteur dans une telle base (ei). Si x est un vecteur, alors :

x=\sum \langle e_i,x\rangle \cdot e_i

Il est tentant de vouloir généraliser ce résultat sur un espace de dimension infinie. Si l'espace fonctionnel dispose de bonnes propriétés une telle approche est possible. C'est le cas, si l'espace est séparable, c'est-à-dire s'il existe une famille dénombrable dense, c'est-à-dire qui permet d'approcher aussi précisément que souhaité tout vecteur. Cette situation est analogue à celles des nombres réels. À une distance arbitrairement petite de tout réel se trouve un nombre rationnel. Le théorème de Stone-Weierstrass montre que tel est le cas sur de très nombreux espaces fonctionnels.

David Hilbert s'est intéressé à une autre propriété : la complétude. À l'image de la situation pour les nombres réels, toute suite de Cauchy converge dans un tel espace. La difficulté réside alors dans la signification à donner à une série contenant à priori un ensemble de terme qui n'a plus aucune raison d'être dénombrable si l'hypothèse de la séparabilité n'est plus remplie. Deux remarques permettent de résoudre cette question. Le cardinal de l'ensemble des termes non nuls est toujours dénombrable. De plus, la convergence de la série est absolue, garantissant ainsi que l'ordre dans lequel les éléments sont pris n'a aucune conséquence sur la limite de la série.

Propriétés

Inégalité de Bessel et coefficients de Fourier

Article détaillé : inégalité de Bessel.

Une première majoration joue un rôle important pour établir les propriétés d'une base de Hilbert. Elle porte le nom d'inégalité de Bessel.

Inégalité de Bessel —  Soient E un sous-espace vectoriel fermé de H, {}^{(f_i)_{i\in I}} une base de Hilbert de E et x un élément de H. Alors l'ensemble de indices i pour lesquels \langle x,f_i\rangle\ne 0 est au plus dénombrable, et la série suivante est convergente et majorée par le carré de la norme de x :

\sum_{i\in I} |\langle x,f_i\rangle |^2 \le \|x\|^2~.

L'égalité n'a lieu que si x est élément de E .

Le cas d'égalité est toujours vérifié si E est égal à H, il prend le nom d'égalité de Parseval. C'est une généralisation du théorème de Pythagore, utilisée dans le cadre des séries de Fourier.

La démonstration de l'inégalité de Bessel contient la propriété suivante :

Proposition — Une famille orthonormale de H est une base de Hilbert si et seulement si elle est totale, c'est-à-dire si le sous-espace vectoriel qu'elle engendre est dense dans H.

Ainsi une base de Hilbert de H n'est pas une base au sens algébrique du terme, mais une base orthonormale d'un sous-espace D dont l'adhérence est égale à H.

L'égalité de Parseval permet de déterminer l'expression d'un élément x dans une base hilbertienne (ei) de H :

Théorème et définition —  Si (ei) est une base hilbertienne de H, l'égalité suivante est vérifiée :

x= \sum_{i\in I} \langle x,e_i\rangle \cdot e_i

Les coefficients \langle x,e_i\rangle sont appelés coefficients de Fourier de x, et constituent l'unique famille de coefficients permettant d'exprimer x dans la base de Hilbert.

Ainsi, à l'image de la situation pour une base au sens algébrique, il existe une et une unique manière d'exprimer un vecteur dans une base de Hilbert, mais en général comme une série et non plus une somme finie.

Existence

L'existence d'une base hilbertienne n'est pas garantie par les axiomes d'un espace préhilbertien. Il faut ajouter au moins une hypothèse pour la démontrer.

Théorème —  Si H est complet ou séparable, alors il existe une base hilbertienne.

Démonstration
  • Si E est complet, alors il existe une base hilbertienne.

Soit F l'ensemble des parties orthonormales de E, muni de la relation d'ordre inductif l'inclusion. Soit m une famille maximale de F. Son existence est garantie par le lemme de Zorn. Notons H l'adhérence du sous-espace vectoriel engendré par m, et montrons que H=E, ce qui prouvera que m est une base hilbertienne.

Soient x un vecteur de E et y son projeté orthogonal sur H (qui existe, d'après la preuve de l'inégalité de Bessel dans le cas général : il n'est donc pas nécessaire de faire appel au théorème du supplémentaire orthogonal). Alors y-x est orthogonal à H donc nul (par maximalité de m), donc x appartient à H, ce qui permet de conclure que H=E.

  • Si E est séparable, alors il existe une base hilbertienne.

La logique possède une analogie avec la démonstration précédente, même si le lemme de Zorn n'est plus nécessaire. Soit (fn) une suite dense dans E, il est possible d'en extraire une sous-suite libre (gn)n>0 telle que l'adhérence du sous-espace vectoriel engendré par les gn soit égale à E. Soit (hn)n>0 la suite construite par récurrence de la manière suivante :

Soit n un entier positif ou nul, on suppose déjà construits h1, ... , hn et on note Hn le sous-espace qu'ils engendrent (donc pour n=0 on ne suppose rien, et H0={0}). Soit y le projeté orthogonal de gn+1 sur Hn (qui existe, d'après la preuve de l'inégalité de Bessel dans le cas fini). Alors le vecteur gn+1-y est non nul. En le divisant par sa norme, on construit un vecteur hn+1 de norme 1 orthogonal à Hn (donc à tous les hi précédents) et tel que l'espace vectoriel engendré par Hn et hn+1 contienne gn+1.

La famille (hn) est orthonormale par construction. Les i premiers vecteurs de cette famille engendrent le même espace que les i premiers vecteurs de la famille (gn), les espaces vectoriels engendrés par (hn) et (gn) sont donc confondus, ce qui achève la démonstration.

Un algorithme, dénommé Procédé de Gram-Schmidt, se fonde sur cette logique.

Exemples

Voici deux exemples de bases hilbertiennes de L2([0,1]) (que l'on peut facilement transformer en bases hilbertiennes de L2([a,b]) pour un intervalle [a,b] arbitraire, par changement de variable).

Système trigonométrique

Article détaillé : série de Fourier.

L'exemple classique de base de Hilbert (et même l'origine du concept) est l'ensemble des fonctions trigonométriques

\{x\mapsto\sqrt2\cos(2\pi nx)~|~n\in\N\}\cup\{x\mapsto\sqrt2\sin(2\pi nx)~|~n\in\N^*\} .

Ces fonctions ne forment pas une base au sens algébrique, car elles ne constituent pas une famille génératrice de L2([0,1]). Plus précisément, elles forment une base du sous-espace des polynômes trigonométriques.

Le fait que cette famille soit totale est connu sous le nom de théorème de Riesz-Fischer.

Système de Haar

La famille d'ondelettes de Haar (ψn,k), indexée par n et k, entiers naturels tels que k < 2n, forme également une base de Hilbert de L2([0,1]). Ces fonctions sont définies à partir de l'ondelette mère ψ donnée par

\psi(x)=\left\{\begin{array}{ll} 1&\textrm{si}\quad0\le x<\frac12,\\ -1&\textrm{si}\quad\frac12\le x<1,\\ 0&\textrm{sinon,}\\ \end{array}\right.

en posant

\psi_{n,k}(x)=2^{n/2}\psi(2^n x-k)~ .

Notes et références

  1. ↑ par exemple voir S. Lang, Analyse réelle, Paris, InterEditions, 1977 (ISBN 2729600595), p. 150
  2. ↑ L. Euler, Démonstration de la somme de cette suite 1 + 1/4 + 1/9 + 1/16 + 1/25 + 1/36 + etc, Journal lit. d'Allemagne, de Suisse et du Nord 2, 1743, p. 115-127
  3. ↑ Pour plus de détails voir : (en) Euler’s Solution of the Basel Problem – The Longer Story par E. Sandifer de l'université de New-York
  4. ↑ J. Fourier, Théorie analytique de la chaleur, Paris, Firmin Didot Père et Fils, 1822, rééd. Jacques Gabay, 1988 (ISBN 2-87647-046-2)

Voir aussi

Bibliographie

Liens externes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Base de Hilbert de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Base De Hilbert — David Hilbert en 1912 Une base de Hilbert ou encore base hilbertienne est une généralisation aux espaces de Hilbert de la notion classique de base orthonormée en algèbre linéaire, pour les espaces euclidiens (ou hermitiens …   Wikipédia en Français

  • Base de hilbert — David Hilbert en 1912 Une base de Hilbert ou encore base hilbertienne est une généralisation aux espaces de Hilbert de la notion classique de base orthonormée en algèbre linéaire, pour les espaces euclidiens (ou hermitiens …   Wikipédia en Français

  • Theoreme de la base de Hilbert — Théorème de la base de Hilbert Cet article court présente un sujet plus amplement développé ici : Anneau noethérien. En théorie des anneaux, le théorème de la base de Hilbert affirme que si A est un anneau noethérien, alors l anneau des… …   Wikipédia en Français

  • Théorème de la base de hilbert — Cet article court présente un sujet plus amplement développé ici : Anneau noethérien. En théorie des anneaux, le théorème de la base de Hilbert affirme que si A est un anneau noethérien, alors l anneau des polynômes en un nombre fini d… …   Wikipédia en Français

  • Théorème de la base de Hilbert — Cet article court présente un sujet plus développé dans : Anneau noethérien. En théorie des anneaux, le théorème de la base de Hilbert affirme que si A est un anneau noethérien, alors l anneau des polynômes en un nombre fini d indéterminées… …   Wikipédia en Français

  • Base hilbertienne — Base de Hilbert David Hilbert en 1912 Une base de Hilbert ou encore base hilbertienne est une généralisation aux espaces de Hilbert de la notion classique de base orthonormée en algèbre linéaire, pour les espaces euclidiens (ou hermitiens …   Wikipédia en Français

  • Base (álgebra) — Saltar a navegación, búsqueda En álgebra lineal, se dice que un conjunto ordenado B es base de un espacio vectorial V si se cumplen las siguientes condiciones: Todos los elementos de la base B deben ser linealmente independientes. Todos los… …   Wikipedia Español

  • Base (Algèbre Linéaire) — Pour les articles homonymes, voir Base. En mathématiques, et plus particulièrement en algèbre linéaire, une base d un espace vectoriel est une famille de vecteurs de cet espace telle que chaque vecteur de l espace puisse être exprimé de manière… …   Wikipédia en Français

  • Base (algebre lineaire) — Base (algèbre linéaire) Pour les articles homonymes, voir Base. En mathématiques, et plus particulièrement en algèbre linéaire, une base d un espace vectoriel est une famille de vecteurs de cet espace telle que chaque vecteur de l espace puisse… …   Wikipédia en Français

  • Base d'un espace — Base (algèbre linéaire) Pour les articles homonymes, voir Base. En mathématiques, et plus particulièrement en algèbre linéaire, une base d un espace vectoriel est une famille de vecteurs de cet espace telle que chaque vecteur de l espace puisse… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”