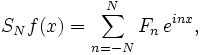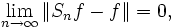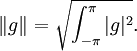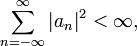Theoreme de Riesz-Fischer
- Theoreme de Riesz-Fischer
-
Théorème de Riesz-Fischer
En mathématiques, le théorème de Riesz-Fischer dit qu'une fonction est de carré intégrable si et seulement si la série de Fourier correspondante converge dans l'espace L2.
Cela signifie que si la somme partielle de la série de Fourier correspondant à la fonction f est donnée par
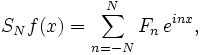
où Fn est le nième coefficient de Fourier donné par
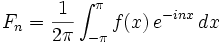 ,
,
alors
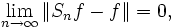
où 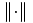 est la norme L2 qui peut s'écrire pour une fonction g
est la norme L2 qui peut s'écrire pour une fonction g
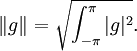
Inversement, si 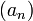 est une suite de nombres complexes indexée par l'ensemble
est une suite de nombres complexes indexée par l'ensemble 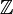 telle que
telle que
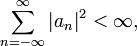
alors il existe une fonction f de carré intégrable telle que les an sont les coefficients de Fourier de f.
Le théorème de Riesz-Fischer généralise l'inégalité de Bessel et peut être utilisé pour démontrer le théorème de Parseval pour les séries de Fourier.
Le mathématicien hongrois Frigyes Riesz et le mathématicien autrichien Ernst Fischer ont démontré de manière indépendante ce théorème en 1907.
Références
- (en) Richard Beals (2004). Analysis: An Introduction. New York: Cambridge University Press. ISBN 0-521-60047-2.
- (en) John Horváth. On the Riesz-Fischer theorem [pdf].
 Portail des mathématiques
Portail des mathématiques
Catégories : Analyse fonctionnelle | Théorème de mathématiques | Espace de Hilbert
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de Riesz-Fischer de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Théorème de riesz-fischer — En mathématiques, le théorème de Riesz Fischer dit qu une fonction est de carré intégrable si et seulement si la série de Fourier correspondante converge dans l espace L2. Cela signifie que si la somme partielle de la série de Fourier… … Wikipédia en Français
Théorème de Riesz-Fischer — Pour les articles homonymes, voir Théorème de Riesz. En mathématiques, plus précisément en théorie de l intégration, le théorème de Riesz Fischer dit : qu une fonction est de carré intégrable si et seulement si la série de Fourier… … Wikipédia en Français
Théorème de Riesz — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Plusieurs noms de théorèmes font référence aux deux frères Riesz, mathématiciens hongrois : Frigyes Riesz Théorème de compacité de Riesz, qui dit qu… … Wikipédia en Français
Théorème de Fischer-Riesz — Théorème de Riesz Fischer En mathématiques, le théorème de Riesz Fischer dit qu une fonction est de carré intégrable si et seulement si la série de Fourier correspondante converge dans l espace L2. Cela signifie que si la somme partielle de la… … Wikipédia en Français
RIESZ (F.) — Les découvertes de Riesz ont exercé une influence profonde sur le développement des mathématiques modernes. Il est, en particulier, le principal fondateur de l’analyse fonctionnelle. Ses mémoires excellent autant par la profondeur et la force des … Encyclopédie Universelle
Théorème de Bessel-Parseval-Plancherel — Égalité de Parseval Pour les articles homonymes, voir Parseval. L égalité de Parseval (parfois appelée également Théorème de Parseval ou Identité de Rayleigh) est une formule fondamentale de la théorie des séries de Fourier. On la doit au… … Wikipédia en Français
Théorème de Parseval — Égalité de Parseval Pour les articles homonymes, voir Parseval. L égalité de Parseval (parfois appelée également Théorème de Parseval ou Identité de Rayleigh) est une formule fondamentale de la théorie des séries de Fourier. On la doit au… … Wikipédia en Français
Fischer — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Fischer », sur le Wiktionnaire (dictionnaire universel) Fischer est le mot allemand équivalent au… … Wikipédia en Français
Frigyes Riesz — (Friedrich en allemand et Frédéric en français), né le 22 juin 1880 à Győr et mort le 28 février 1956 à Budapest, est un mathématicien hongrois. Il a étudié à Budapest, Göttinge … Wikipédia en Français
Ernst Sigismund Fischer — (* 12. Juli 1875 in Wien; † 14. November 1954 in Köln) war ein österreichischer Mathematiker, der sich mit Analysis und Algebra beschäftigte. Inhaltsverzeichnis 1 Leben und Wirken 2 Literatur … Deutsch Wikipedia
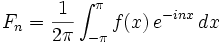 ,
,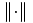 est la norme L2 qui peut s'écrire pour une fonction g
est la norme L2 qui peut s'écrire pour une fonction g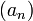 est une suite de nombres complexes indexée par l'ensemble
est une suite de nombres complexes indexée par l'ensemble 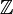 telle que
telle que