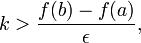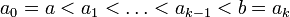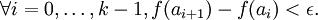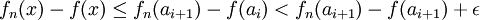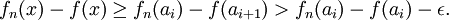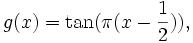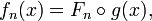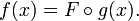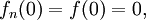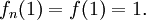Théorème de Dini

Théorèmes de Dini

En topologie, les théorèmes de Dini énoncent des conditions sous lesquelles la convergence simple implique la convergence uniforme. Ce théorème porte le nom du mathématicien italien Ulisse Dini (14 novembre 1845 - 28 octobre 1918)

Sommaire

1 Énoncés des théorèmes de Dini
2 Démonstrations
3 Notes et références
4 Voir aussi

Énoncés des théorèmes de Dini

Les espaces de fonctions réelles peuvent être munis de topologies différentes, à lesquelles sont associées des notions différentes de convergence de fonction, dont la convergence simple et la convergence uniforme :

La convergence simple et la convergence uniforme ne nécessitent aucune structure particulière sur l'ensemble de définition. La convergence simple est en général plus facile à obtenir que la convergence uniforme. Malheureusement, elle ne préserve pas la continuité : la limite simple de fonctions continues définies sur un espace topologique n'est pas continue en général.
La convergence uniforme se définit pour des suites de fonctions définies sur un espace quelconque, à valeurs dans un espace métrique (ou plus généralement, dans un espace uniforme, comme un groupe topologique). Plus difficile à prouver, la convergence uniforme offre l'avantage de préserver la continuité : la limite uniforme de fonctions continues à valeurs dans un espace métrique est continue.

La convergence uniforme implique la convergence simple, mais l'inverse est faux dès que l'espace de départ est infini. Les théorèmes de Dini donnent des conditions sous lesquelles la convergence simple d'une suite de fonctions réelles implique sa convergence uniforme. Ce sont donc des outils très efficaces en pratique pour prouver qu'une suite de fonctions converge uniformément. Les théorèmes de Dini demandent que l'espace de départ possède une structure particulière, et que l'espace d'arrivée soit $\R$ .

Le premier théorème de Dini peut être vu comme une version pour les intégrales de Riemann du théorème de convergence monotone.

Premier théorème

Le premier théorème s'énonce :

La convergence simple d'une suite monotone de fonctions définies et continues sur un espace compact vers une fonction continue implique sa convergence uniforme.

Formellement, on dispose d'un espace topologique X, d'une suite de fonctions 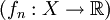$(f_n:X\rightarrow \R)$ , et on fait les hypothèses suivantes :

Continuité : Les fonctions $f n$ et la fonction f sont continues sur X ;
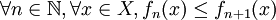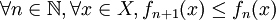Monotonie : la suite $(f n)$ est soit croissante ( $\forall n\in\N, \forall x\in X, f_n(x)\leq f_{n+1}(x)$ ), soit décroissante ( $\forall n\in\N, \forall x\in X, f_{n+1}(x) \leq f_n(x)$ ) ;
Compacité : X est compact et donc de tout recouvrement ouvert de X on peut extraire un sous-recouvrement fini.
Convergence simple : Pour tout x de X, la suite de réels $(f n (x))$ converge vers $f (x)$ .

On en déduit alors que la suite $(f n)$ converge uniformément sur X vers f.

Deuxième théorème

Le deuxième théorème de Dini s'énonce ainsi :

La convergence simple d'une suite de fonctions réelles d'une variable réelle définies et croissantes sur un intervalle $[a, b]$ de R vers une fonction continue sur $[a, b]$ implique la convergence uniforme.

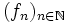Formellement, on dispose d'un intervalle $[a, b]$ de $\R$ et d'une suite $(f_{n})_{n \in \N}\,$ de fonctions (non-nécessairement continues) de $[a, b]$ dans $\R$ . On fait les hypothèses suivantes :

Continuité : La fonction f est continue ;
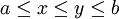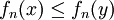Monotonie : Pour tout entier n et pour tout couple $(x, y)$ tel que $a\leq x\leq y\leq b$ , on a : $f_n(x)\leq f_n(y)$ ;
Convergence simple : Pour tout x de $[a, b]$ , la suite de réels 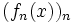$(f_{n}(x))_{n}\,$ converge vers $f\,(x)$ .

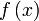On en déduit que la suite 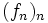$(f_{n})_{n}\,$ converge uniformément sur $[a, b]$ vers la fonction $f\,$ .

Bien que connu sous le nom de deuxième théorème de Dini dans l'enseignement francophone, il semble qu'en fait ce théorème soit dû à Pólya^[1].

Convergence uniforme des fonctions de répartitions

Le deuxième théorème de Dini possède un corollaire précieux en probabilités et en statistique:

Une suite de fonctions de répartition qui converge simplement sur R vers une fonction de répartition continue F, converge uniformément vers F sur R.

En conséquence, la convergence uniforme des fonctions de répartitions a lieu dans le cas du théorème de la limite centrale, où la fonction de répartition limite est celle de la loi normale, et est, à ce titre, continue. Cela a des conséquences non anecdotiques en probabilités et statistique, comme, par exemple, le théorème de la limite centrale pour la médiane, ou bien le théorème de la limite centrale pour les processus de renouvellement.

Un détour par l'équicontinuité

Le premier théorème de Dini peut se déduire, via le lemme suivant, du théorème d'Ascoli, ou simplement d'une propriété fondamentale de l'équicontinuité qu'on utilise pour prouver ce dernier.

La convergence simple d'une suite monotone de fonctions continues vers une fonction continue implique son équicontinuité.

Notons que dans ce lemme purement local, l'espace de départ n'est pas supposé compact.

Démonstrations

Les démonstrations proposées reprennent les notations introduites ci-dessus.

Du premier théorème

Supposons que la suite $(f n)$ est décroissante (si elle est croissante, on se ramène au cas décroissant en remplaçant les fonctions $f n$ et $f$ par leurs opposées) et que de plus f=0 (on s'y ramène en remplaçant les $f n$ par $f n - f$ ).

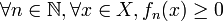On a alors $\forall n\in\N, \forall x\in X, f_n(x)\geq 0$ .

Fixons un nombre réel $ε > 0$ et considérons les ensembles 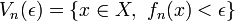$V_n(\epsilon)=\{x\in X,\ f_n(x)<\epsilon\}$ . Par continuité des fonctions $f n$ , ces ensembles sont des ouverts (en fait il suffirait, dans le cas décroissant, de supposer les $f n$ semi-continues supérieurement et $f$ semi-continue inférieurement). La convergence simple de $(f n)$ vers 0 se traduit par :

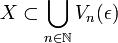$X \subset \bigcup_{n \in \N} V_{n}(\epsilon)$ .

Comme X est compact, on peut extraire un sous-recouvrement fini ; il existe donc un entier $N ε$ tel que

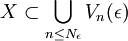$X \subset \bigcup_{n \leq N_\epsilon} V_n(\epsilon)$ .

Par monotonie, la suite $V n (ε)$ est croissante. Il vient donc :

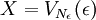$X=V_{N_\epsilon}(\epsilon)$ .

A nouveau en utilisant l'hypothèse de monotonie,

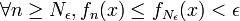$\forall n\geq N_\epsilon, f_n(x)\leq f_{N_\epsilon}(x)<\epsilon$ .

Donc la convergence de $(f n)$ vers 0 est uniforme sur X.

Du deuxième théorème

Soit un réel $ε > 0$ . La fonction $f$ est non seulement continue et bornée (par hypothèse) mais aussi croissante (comme limite simple de fonctions croissantes). En choisissant

$k>{f(b)-f(a)\over\epsilon},$

il existe une subdivision

$a_0=a< a_1<\dots< a_{k-1}<b=a_k$

de $[a, b]$ telle que

$\forall i=0,\ldots,k-1, f(a_{i+1})-f(a_i)<\epsilon.$

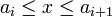Pour tout $x\in[a,b]$ , soit $i$ tel que $a_i\leq x\leq a_{i+1}$ . La croissance de $f$ et des $f n$ et le choix de la subdivision impliquent (pour tout entier $n$ )

$f_n(x)-f(x)\leq f_n(a_{i+1})-f(a_i)<f_n(a_{i+1})-f(a_{i+1})+\epsilon$

$f_n(x)-f(x)\geq f_n(a_i)-f(a_{i+1})>f_n(a_i)-f(a_i)-\epsilon.$

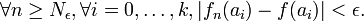
Par convergence simple, il existe un entier $N ε$ tel que $\forall n\geq N_\epsilon,\forall i=0,\dots,k, |f_n(a_i)-f(a_i)|<\epsilon.$

Les inégalités précédentes donnent alors : $\forall n\geq N_\epsilon,\forall x\in[a,b], |f_n(x)-f(x)|< 2\epsilon.$

Donc la convergence de $(f n)$ vers $f$ est uniforme sur $[a, b]$ .

De la convergence uniforme des fonctions de répartitions

Notons $(F n) n$ la suite de fonctions de répartition qui converge vers $F$ . Pour $x\in]0,1[$ , posons, par exemple:

$g(x)=\tan(\pi(x-{1\over 2})),$

puis

$f_n(x)=F_n\circ g(x),$

$f(x)=F\circ g(x).$

Posons aussi:

$f_n(0)=f(0)=0,\,$

$f_n(1)=f(1)=1.\,$

Ainsi

$f n$ est croissante sur [0,1], parce que $F n$ et $g$ sont croissantes (sur $\R$ et ]0,1[, respectivement) ;
$f n$ converge simplement vers $f$ sur ]0,1[, parce que $F n$ converge simplement vers $F$ sur $\R$ ;
par propriété des fonctions de répartition, et comme la limite de $g$ en 0 (resp. en 1) est $-\infty$ (resp. $+\infty$ ), on en déduit que $f$ est continue en 0 et en 1 ;
$f$ est continue sur ]0, 1[ comme composée des fonctions continues $F$ et $g$ .

Ainsi $f n$ converge uniformément vers $f$ en vertu du deuxième théorème de Dini. La convergence uniforme de $F n$ vers $F$ en découle.

Du détour par l'équicontinuité

Supposons, comme dans la preuve du premier théorème, que la suite $(f n)$ est décroissante et converge simplement vers $0$ .

Fixons un un point $x$ de $X$ et un nombre réel $ε > 0$ . Puisque $f n (x)$ tend vers $0$ , il existe un entier $n$ tel que $f n (x) < ε$ .

Par continuité en x de 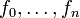$f_0,\ldots,f_n$ , il existe un voisinage $V$ de $x$ tel que pour tout point $y$ de $V$ ,

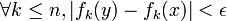$\forall k\leq n,|f_k(y)-f_k(x)|<\epsilon$ .

On en déduit en particulier $f n (y) < 2ε$ , d'où (par décroissance de la suite $(f n)$ )

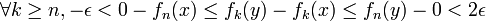$\forall k\geq n, -\epsilon<0-f_n(x)\leq f_k(y)-f_k(x)\leq f_n(y)-0< 2\epsilon$ ,

si bien que finalement

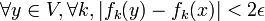$\forall y\in V, \forall k,|f_k(y)-f_k(x)|<2\epsilon$ ,

ce qui prouve l'équicontinuité au point $x$ de la suite $(f n)$ .

Notes et références

↑ Pólya-Szegö, Problems and Theorems in Analysis

Voir aussi

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8mes de Dini ».

Catégories : Compacité | Analyse fonctionnelle | Théorème de mathématiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Dini de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Theoreme de la limite centrale — Théorème de la limite centrale Pour les articles homonymes, voir TCL. Le théorème de la limite centrale (appelé plus correctement théorème central limite, sans e à central puisque c est le théorème qui est central) est un résultat sur la… … Wikipédia en Français
Théorème de la limite centrale — Pour les articles homonymes, voir TCL. Le théorème de la limite centrale (appelé plus correctement théorème central limite, sans e à central puisque c est le théorème qui est central) est un résultat sur la convergence en probabilités d une suite … Wikipédia en Français
Théorème de la limite centrée — Théorème de la limite centrale Pour les articles homonymes, voir TCL. Le théorème de la limite centrale (appelé plus correctement théorème central limite, sans e à central puisque c est le théorème qui est central) est un résultat sur la… … Wikipédia en Français
Théorème de Glivenko-Cantelli — Le théorème de Glivenko Cantelli est parfois appelé « le théorème fondamental de la statistique » car il exprime en quoi une loi de probabilité peut être révélée par la connaissance d un (grand) échantillon de ladite loi de probabilité … Wikipédia en Français
Théorème central limite — Pour les articles homonymes, voir TCL. La loi normale, souvent appelée la « courbe en cloche » Le théorème central li … Wikipédia en Français
Théorème de Mercer — En mathématiques et plus précisément en analyse fonctionnelle, le théorème de Mercer est une représentation d une fonction symétrique de type positif par le carré d une série convergente de produits de fonctions. Ce théorème est l un des… … Wikipédia en Français
Theoremes de Dini — Théorèmes de Dini En topologie, les théorèmes de Dini énoncent des conditions sous lesquelles la convergence simple implique la convergence uniforme. Ce théorème porte le nom du mathématicien italien Ulisse Dini (14 novembre 1845 28 octobre 1918) … Wikipédia en Français
Théorèmes de Dini — Pour les articles homonymes, voir Dini. En mathématiques, et plus précisément en topologie, les théorèmes de Dini énoncent des conditions sous lesquelles la convergence simple implique la convergence uniforme. Ces théorèmes portent le nom du… … Wikipédia en Français
Théorèmes de dini — En topologie, les théorèmes de Dini énoncent des conditions sous lesquelles la convergence simple implique la convergence uniforme. Ce théorème porte le nom du mathématicien italien Ulisse Dini (14 novembre 1845 28 octobre 1918) Sommaire 1… … Wikipédia en Français
Dérivées de Dini — Pour les articles homonymes, voir Dini. Les dérivées de Dini sont quatre nombres introduits par le mathématicien Ulisse Dini pour généraliser la notion de dérivée d une fonction lorsque celle ci n est pas dérivable. Sommaire 1 Définition … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème de Dini

Théorèmes de Dini

Sommaire