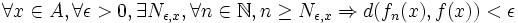- Convergence Simple
-
Convergence simple
En mathématiques, la convergence simple ou ponctuelle est une notion de convergence dans un espace fonctionnel, c’est-à-dire dans un ensemble de fonctions entre deux espaces topologiques. C'est une définition peu exigeante : elle est plus facile à établir que d'autres formes de convergence, notamment la convergence uniforme et le passage à la limite possède donc moins de propriétés : une suite de fonctions continues peut ainsi converger simplement vers une fonction qui ne l'est pas.
Sommaire
Définition
Convergence simple
- Soient
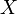 et
et 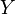 deux espaces topologiques, soit
deux espaces topologiques, soit 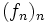 une suite de fonctions définies sur
une suite de fonctions définies sur 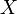 à valeurs dans
à valeurs dans 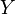 . On dit que la suite de fonctions
. On dit que la suite de fonctions 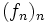 converge simplement si :
converge simplement si :
-
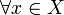 , la suite
, la suite 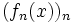 converge dans
converge dans 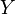
- Si l'application
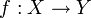 est telle que
est telle que 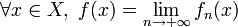 on dit que la suite de fonctions
on dit que la suite de fonctions 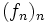 converge simplement vers la fonction
converge simplement vers la fonction  , ou que f est 'limite simple' de la suite
, ou que f est 'limite simple' de la suite 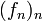 .
.
Remarque
Si l'espace Y est supposé séparé, l'éventuelle limite simple d'une suite de fonctions à valeurs dans Y est toujours unique.
Il convient également de remarquer que la topologie de l'espace de départ X n'intervient pas du tout dans la définition : on peut donc se passer de structure topologique sur celui-ci, et définir cette notion pour tout ensemble X.
Topologie faible
Définition
Il existe une topologie associée à la convergence simple, on l'appelle en général topologie faible. Cette topologie est souvent définie à l'aide d'une base de voisinages. On la définit de la manière suivante:
Soit
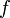 une fonction de
une fonction de 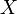 dans
dans 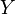 deux espaces topologiques tel que
deux espaces topologiques tel que 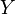 soit séparé. Soit
soit séparé. Soit 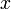 un élément de
un élément de 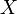 tel que
tel que 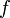 soit définie en
soit définie en 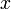 . On considère alors
. On considère alors 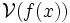 une base de voisinage de
une base de voisinage de 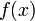 pour la topologie de
pour la topologie de 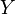 . À chaque élément
. À chaque élément 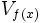 de
de 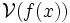 on associe le sous ensemble
on associe le sous ensemble 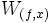 des fonctions
des fonctions 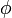 de
de 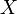 dans
dans 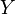 définies en
définies en 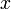 et tel que
et tel que 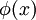 soit élément de
soit élément de 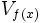 . L'union de tous les ensembles de type
. L'union de tous les ensembles de type 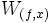 quand
quand 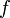 parcourt l'ensemble des fonctions et
parcourt l'ensemble des fonctions et 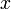 parcourt le domaine de définition de
parcourt le domaine de définition de 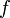 forme une base de voisinage. La topologie associée est appelée la topologie faible.
forme une base de voisinage. La topologie associée est appelée la topologie faible.Remarques
On peut démontrer que la convergence simple d'une suite de fonctions
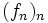 est équivalent à la convergence pour la topologie faible de la suite.
est équivalent à la convergence pour la topologie faible de la suite.Si
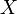 n'est pas un ensemble fini, alors il n'existe pas de distance associée à cette topologie. Nous savons en effet que tout espace métrique est muni d'une topologie déduite. Cette topologie ne peut jamais être la topologie faible.
n'est pas un ensemble fini, alors il n'existe pas de distance associée à cette topologie. Nous savons en effet que tout espace métrique est muni d'une topologie déduite. Cette topologie ne peut jamais être la topologie faible.Propriétés
La topologie faible est un critère de convergence peu contraignant comme son nom l'indique. Il existe donc moins de propriétés que dans le cas de la convergence uniforme par exemple.
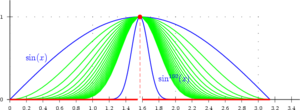
- La convergence uniforme implique la convergence simple. La démonstration découle directement des définitions. En revanche la réciproque est fausse comme le montre le contre-exemple illustré graphiquement en début d'article.
- La convergence simple ne conserve pas la continuité, comme le montre le contre-exemple illustré graphiquement en début d'article.
- Dans le cas où l'ensemble de départ est un espace mesurable et où l'ensemble d'arrivée est le corps des réels alors la convergence simple peut indiquer la convergence pour la norme L1 avec l'ajout de certaines hypothèses décrites dans les articles Théorème de convergence monotone et Théorème de convergence dominée.
- Le passage à la limite pour l'intégrale des limites simples a contribué à motiver l'introduction par Henri Lebesgue de sa notion de fonction mesurable. La préservation de l'intégrabilité locale n'est en effet pas vrai au sens de Riemann employé dans le cadre de la théorie de l'intégrale de Riemann.
Convergence simple dans un espace métrique
On suppose maintenant que
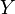 est un espace métrique, c'est-à-dire que
est un espace métrique, c'est-à-dire que 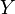 est muni d'une distance
est muni d'une distance 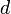 et de la topologie qui lui est associée. On sait d'abord qu'un espace métrique est toujours séparé. On peut alors traduire la notion de convergence simple en termes de « epsilon »:
et de la topologie qui lui est associée. On sait d'abord qu'un espace métrique est toujours séparé. On peut alors traduire la notion de convergence simple en termes de « epsilon »:Une suite de fonctions
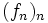 converge simplement sur
converge simplement sur 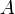 vers une fonction
vers une fonction  si et seulement si :
si et seulement si :Voir aussi
- convergence uniforme
- limite (mathématiques)
- Théorème d'Egoroff
- Théorème de la limite simple de Baire
- Portail des mathématiques
Catégories : Analyse fonctionnelle | Espace topologique remarquable | Analyse réelle - Soient
Wikimedia Foundation. 2010.