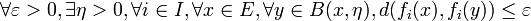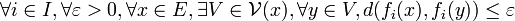Equicontinuite

Équicontinuité

En analyse, une famille de fonctions est dite équicontinue si toutes les fonctions sont continues et ont des variations sensiblement équivalentes sur un voisinage donné.

Par exemple, si une suite de fonctions continues converge simplement vers une fonction, cette fonction n'est pas forcément continue (un contre-exemple est donné par la famille de fonctions définies sur $[0,1]$ par 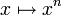$x \mapsto x^n$ ). Cependant, si cette suite est équicontinue, alors on peut conclure que la limite est continue.

Définitions

Soit 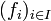$(f_i)_{i \in I}$ une famille de fonctions d'un espace topologique E dans un espace métrique F.

La famille 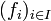$(f_i)_{i \in I}$ est dite équicontinue si et seulement si :

$\forall \varepsilon > 0, \forall x \in E, \exists V\in\mathcal{V}(x), \forall i \in I, \forall y \in V, d(f_i(x),f_i(y)) \leq \varepsilon$

Lorsque la topologie sur E est associée à une distance, la famille 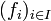$(f_i)_{i \in I}$ est dite uniformément équicontinue si et seulement si :

$\forall \varepsilon > 0, \exists \eta > 0, \forall i \in I, \forall x \in E, \forall y \in B(x,\eta), d(f_i(x),f_i(y)) \leq \varepsilon$

À titre de comparaison, la quantification de la phrase suivante : "les fonctions $f i$ sont toutes continues" s'écrit :

$\forall i \in I, \forall \varepsilon > 0, \forall x \in E, \exists V\in\mathcal{V}(x), \forall y \in V, d(f_i(x),f_i(y)) \leq \varepsilon$

Tout dépend de l'ordre des quantificateurs, pour la continuité, V dépend de $\varepsilon$ , x et de i. Pour l'équicontinuité, V dépend seulement de $\varepsilon$ et de x, alors que l'hypothèse d'uniforme équicontinuité, la plus forte, ne fait dépendre le module d'équicontinuité $η$ que de $\varepsilon$ .

Interprétation

Etant donnée la famille 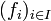$(f_i)_{i \in I}$ , on peut considérer l'application de l'espace $E$ dans l'ensemble $F I$ qui à tout $x\in E$ associe la famille 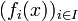$(f_i(x))_{i\in I}$ .

L'équicontinuité (resp. l'équicontinuité uniforme) de la famille 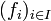$(f_i)_{i \in I}$ équivaut à la continuité (resp. à la continuité uniforme) de cette application de $E$ dans $F I$ lorsqu'on munit $F I$ de la topologie de la convergence uniforme sur $I$ , c'est-à-dire la topologie définie par la distance de la convergence uniforme

(cette distance $δ$ sur $F I$ est définie par $\delta(u,v)=\min(1,\sup_{i\in I}d(u_i,v_i))$ ),

tandis que la continuité de chacune des $f i$ équivaut à la continuité de cette application de $E$ dans $F I$ lorsqu'on munit $F I$ de la topologie de la convergence simple sur $I$ , qui n'est autre que la topologie produit.

Propriétés

1) Si une suite $(f n)$ de fonctions est équicontinue et converge simplement alors la limite simple est continue. Plus généralement, si A est un ensemble équicontinu de fonctions de E dans F alors son adhérence dans l'espace produit $F E$ (qui n'est autre que l'espace des applications de E dans F muni de la topologie de la convergence simple) est encore équicontinue.

2) Si une suite $(f n)$ de fonctions est équicontinue et converge simplement sur un sous-ensemble dense de l'espace de départ, et si l'espace d'arrivée est complet, alors la suite converge simplement sur l'espace de départ tout entier (donc la propriété précédente s'applique).

3) Si une famille de fonctions définies sur un espace métrique compact est équicontinue, alors elle est uniformément équicontinue (application directe du théorème de Heine, via l'interprétation ci-dessus).

4) Si une suite $(f n)$ de fonctions est équicontinue et converge simplement alors cette convergence est uniforme sur tout compact. Plus généralement, si K est un espace compact et si A est un ensemble équicontinu de fonctions de K dans F alors sur A, la topologie de la convergence simple et celle de la convergence uniforme coïncident.

5) Théorème d'Ascoli : Si K est un espace compact, F un espace métrique, et A une partie de l'espace des fonctions continues de K dans F (muni de la distance uniforme), alors A est relativement compacte si et seulement si A est équicontinue et pour tout 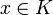$x \in K$ , l'ensemble 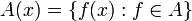$A(x) = \{f(x) : f \in A\}$ est relativement compact dans F.

Démonstration de la propriété 4

Soient A équicontinu sur un compact K et f un élément de A. Pour toute partie I de K, notons

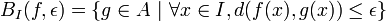$B_I(f,\epsilon)=\{g\in A\ |\ \forall x\in I, d(f(x),g(x))\le\epsilon\}$ .

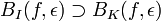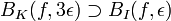Une base de voisinages de f dans A pour la topologie de la convergence uniforme (resp. simple) est donnée par les $B K (f,ε)$ pour tout réel $ε > 0$ (resp. les $B I (f,ε)$ pour tout réel $ε > 0$ et toute partie finie I de K). On a évidemment $B_I(f,\epsilon)\supset B_K(f,\epsilon)$ . Montrons que réciproquement, pour tout réel $ε > 0$ , il existe une partie finie I de K telle que $B_K(f,3\epsilon)\supset B_I(f,\epsilon)$ .

Par équicontinuité de A, tout point x de K appartient à un ouvert $O x$ tel que pour tout g de A (en particulier pour g=f)

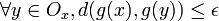$\forall y\in O_x, d(g(x),g(y))\le\epsilon$ .

Par compacité, K est recouvert par un nombre fini de ces ouverts $O x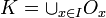$ : $K=\cup_{x\in I}O_x$ pour une certaine partie finie I de K.

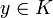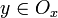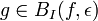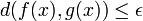Pour tout $y\in K$ , soit $x\in I$ tel que $y\in O_x$ . Pour tout $g\in B_I(f,\epsilon)$ on a $d(f(x),g(x))\leq\epsilon$ , d'où

$d(f(y),g(y))\leq d(f(y),f(x))+d(f(x),g(x))+d(g(x),g(y))\le 3\epsilon,$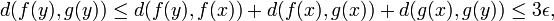

d'où l'inclusion voulue.

Portail des mathématiques

Ce document provient de « %C3%89quicontinuit%C3%A9 ».

Catégorie : Analyse fonctionnelle

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Equicontinuite de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

Équicontinuité — En analyse, une famille de fonctions est dite équicontinue si toutes les fonctions sont continues et ont des variations sensiblement équivalentes sur un voisinage donné. Par exemple, si une suite de fonctions continues converge simplement vers… … Wikipédia en Français
Équicontinu — Équicontinuité En analyse, une famille de fonctions est dite équicontinue si toutes les fonctions sont continues et ont des variations sensiblement équivalentes sur un voisinage donné. Par exemple, si une suite de fonctions continues converge… … Wikipédia en Français
Theoremes de Dini — Théorèmes de Dini En topologie, les théorèmes de Dini énoncent des conditions sous lesquelles la convergence simple implique la convergence uniforme. Ce théorème porte le nom du mathématicien italien Ulisse Dini (14 novembre 1845 28 octobre 1918) … Wikipédia en Français
Théorème de Dini — Théorèmes de Dini En topologie, les théorèmes de Dini énoncent des conditions sous lesquelles la convergence simple implique la convergence uniforme. Ce théorème porte le nom du mathématicien italien Ulisse Dini (14 novembre 1845 28 octobre 1918) … Wikipédia en Français
Théorèmes de Dini — Pour les articles homonymes, voir Dini. En mathématiques, et plus précisément en topologie, les théorèmes de Dini énoncent des conditions sous lesquelles la convergence simple implique la convergence uniforme. Ces théorèmes portent le nom du… … Wikipédia en Français
Théorèmes de dini — En topologie, les théorèmes de Dini énoncent des conditions sous lesquelles la convergence simple implique la convergence uniforme. Ce théorème porte le nom du mathématicien italien Ulisse Dini (14 novembre 1845 28 octobre 1918) Sommaire 1… … Wikipédia en Français
Theoreme d'Ascoli — Théorème d Ascoli En analyse fonctionnelle, le théorème d Ascoli est un puissant résultat caractérisant les parties relativement compactes de l espace des fonctions continues définies sur un espace compact à valeurs dans un espace métrique. Il se … Wikipédia en Français
Théorème d'Arzelà-Ascoli — Théorème d Ascoli En analyse fonctionnelle, le théorème d Ascoli est un puissant résultat caractérisant les parties relativement compactes de l espace des fonctions continues définies sur un espace compact à valeurs dans un espace métrique. Il se … Wikipédia en Français
Théorème d'Ascoli — En analyse fonctionnelle, le théorème d Ascoli, ou théorème d Arzelà Ascoli, démontré par les mathématiciens italiens Giulio Ascoli et Cesare Arzelà (en), caractérise les parties relativement compactes de l espace des fonctions continues d… … Wikipédia en Français
Critère de Nagumo — Dans le cadre des équations différentielles, le critère de Nagumo est un critère plus faible que le théorème de Cauchy Lipschitz donnant, tout comme le théorème de Cauchy Lipschitz, une condition suffisante pour garantir l existence et l unicité… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Equicontinuite

Équicontinuité

Sommaire

Définitions

Interprétation

Propriétés

Démonstration de la propriété 4

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Equicontinuite

Équicontinuité

Sommaire

Définitions

Interprétation

Propriétés

Démonstration de la propriété 4

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link