- Tenseur de bel-robinson
-
Tenseur de Bel-Robinson
Articles scientifiques
sur les tenseursGénéralitésMathématiquesTenseur (mathématiques)
Produit tensoriel
... de deux modules
... de deux applications linéaires
Algèbre tensorielle
Champ tensoriel
Espace tensorielPhysiqueConvention d'Einstein
Tenseur métrique
Tenseur énergie-impulsion
Tenseur de Riemann
... de Ricci
... d'Einstein
... de Weyl
... de Levi-Civita
... de Killing
... de Killing-Yano
... de Bel-Robinson
... de Cotton-York
Tenseur électromagnétique
Tenseur des contraintes
Tenseur des déformationsArticles connexesPortail des MathématiquesPortail de la PhysiqueEn relativité générale, le tenseur de Bel-Robinson, du nom de Lluis Bel et Ivor Robinson[1] est un tenseur conçu en suivant une procédure assimilable à celle du tenseur énergie-impulsion en électromagnétisme. Ce tenseur présente certaines propriétés qui lui confèrent une analogie avec le tenseur énergie-impulsion d'un champ gravitationnel, quoiqu'une telle quantité ne puisse être définie en relativité générale.
Sommaire
Formule
Le tenseur de Bel-Robinson, en général noté T est défini à partir du tenseur de Weyl par l'un ou l'autre des formules équivalentes :
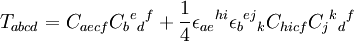 ,
,![T_{abcd} = C_{aecf} C_b{}^e{}_d{}^f - \frac{3}{2} g_{a[b} C_{jk]cf} C^{jk}{}_d{}^f](/pictures/frwiki/99/cef8cb4a710d727b4cbce8e6f032f40c.png) .
.
Propriétés
- Le tenseur de Bel-Robinson est complètement symétrique (il est invariant par échange de ses indices).
- Sa trace (calculée par rapport à n'importe quelle paire d'indices, puisque le tenseur est symétrique) est nulle :
- Taacd = 0,
- Dans le vide, c'est-à-dire quand le tenseur de Riemann est nul, la divergence du tenseur est nulle :
- DaTabcd = 0.
- La composante temporelle du tenseur, c'est-à-dire la quantité Tabcduaubucud, où u est la quadrivitesse d'un observateur, est positive ou nulle, évoquant une densité d'énergie.
Notes
- ↑ Lluis Bel, Comptes rendus de l'Académie des sciences, 247, 1094 (1958) ; Lluis Bel, Comptes rendus de l'Académie des sciences, 248, 1297 (1959) ; Ivor Robinson, notes non publiées (1958) ; Ivor Robinson, On the Bel-Robinson tensor, Classical and Quantum Gravity, 14, A331-A333 (1997) Voir en ligne (accès restreint).
Références
- (en) Robert M. Wald, General Relativity, University of Chicago Press, 1984, 498 pages (ISBN 0226870332), page 90.
- (en) Stanley Deser, The Immortal Bel-Robinson Tensor, communication au colloque Iberian Gravity Symposium, In Gravitation and Relativity in General, World Scientific, Singapour (1999), gr-qc/9901007 Voir en ligne.
- Portail de la physique
Catégorie : Relativité générale
Wikimedia Foundation. 2010.
