Singe savant

Avec suffisamment de temps, un chimpanzé comme celui-ci, qui tape au hasard sur le clavier d’une machine à écrire, pourra presque sûrement produire une copie d’une pièce de théâtre de Shakespeare.

Le paradoxe du singe savant est un théorème selon lequel un singe qui tape indéfiniment et au hasard sur le clavier d’une machine à écrire pourra presque sûrement écrire tous les livres de la Bibliothèque nationale de France. Dans l’adaptation du théorème en langue anglaise, le singe pourra presque sûrement dactylographier tous les travaux réunis de William Shakespeare.

Le résultat fut présenté par Émile Borel en 1909 dans son livre de probabilités. Ces « singes » ne sont pas des singes réels, et ne se comportent pas comme de vrais singes ; ils sont plutôt une métaphore vivante pour une machine abstraite à produire des lettres dans un ordre aléatoire, par exemple un ordinateur ou un générateur aléatoire connecté à une imprimante.

Variante

D'après une formulation populaire du théorème, une infinité de singes dactylographiant pendant une durée infinie produiront un texte donné. Insister sur les deux infinis est cependant excessif. Un seul singe immortel qui tape indéfiniment dactylographiera n'importe quel texte fini, et même obtiendra ce texte une infinité de fois.

Démonstration

Commençons par préciser ce que l'on entend par « événements indépendants » (ici, les touches choisies successivement par le singe, qui sont censées être choisies « indépendamment » les unes des autres, c’est-à-dire que le choix de la lettre suivante ne dépend pas des lettres précédentes ; c'est le cas par exemple si le singe a une mémoire de poisson rouge). Deux événements sont dits indépendants si la probabilité pour que tous deux se produisent est égale au produit des probabilités pour que chaque événement se produise. Par exemple, si la probabilité pour qu’il pleuve sur Sydney un jour particulier est de 0,3 et la probabilité pour qu’il y ait un tremblement de terre à San Francisco un jour particulier est de 0,8, alors la probabilité pour que tous les deux se produisent le même jour est égale à 0,3 × 0,8 = 0,024.

Supposons maintenant que la machine à écrire soit pourvue de 50 touches, et que le mot à taper soit « banane ». En tapant au hasard, il y a une chance sur 50 que la première lettre tapée soit b ; de même, il y a une chance sur 50 que la deuxième lettre tapée soit a, et ainsi de suite. Ces événements sont indépendants, et ainsi il y a une chance sur 50⁶ que les six lettres du mot « banane » soient tapées. Pour la même raison, il y a à nouveau une chance sur 50⁶ que les six lettres suivantes soient celles du mot « banane », et ainsi de suite.

La probabilité de ne pas taper « banane » dans un de ces blocs consécutifs de 6 lettres est de 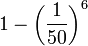. Comme chaque bloc est tapé indépendamment, la probabilité P_n qu'il n'y ait pas « banane » parmi les n premiers blocs de 6 lettres est .

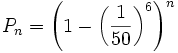Quand n devient très grand, P_n se rapproche de 0 (c'est une suite géométrique). Pour un entier n égal à un million, P_n est égal à 0,9999, pour un n égal à 10 milliards, P_n vaut 0,53 et pour un n égal à 100 milliards, il vaut 0,0017. On dit que la probabilité P_n tend vers zéro quand n tend vers l’infini.

Ainsi, la probabilité que le singe n'ait pas tapé « banane » après 6n frappes est toujours plus petite que P_n (P_n est la probabilité que le singe n'ait pas tapé « banane » dans un des blocs consécutifs de 6 lettres ; si par exemple le singe commence en tapant « abanane », il a effectivement tapé « banane », mais il n'a pas tapé « banane » dans un des blocs qu'on a considérés). Comme P_n tend vers 0, en passant à la limite, on trouve :

La probabilité que le singe ne tape jamais « banane » vaut 0.

C'est dire que, presque sûrement, le singe tape le mot « banane » à un moment. (on peut même dire qu'il tape le mot « banane » dans un de nos blocs de 6 caractères).

L'argument précédent reste valable pour toute chaîne de caractères finie, et pour toute taille de clavier.

Pourquoi dire « presque sûrement » alors que l'événement est de probabilité égale à 1 ? Comment un événement possible peut-il être de probabilité nulle ? Il y a une subtilité due au fait que l'ensemble des résultats possibles (ici l'ensemble de toutes les chaînes de caractères infinies) est infini. Ainsi par exemple, l'événement « le singe ne tape que des "a" » fait partie des événements possibles, mais est de probabilité nulle, tout comme l'événement « le singe ne tape jamais le mot "banane" », comme on vient de le voir.

En pratique

Sans tenir compte de la ponctuation, ni des espaces, ni de la casse, un singe a une chance sur 26 de dactylographier correctement la première lettre du mot Hamlet. Il a une chance sur 676 (26 fois 26) de dactylographier les deux premières lettres. Puisque la probabilité diminue exponentiellement, pour 20 lettres elle ne sera seulement que d’une chance sur 26²⁰ = 19 928 148 895 209 409 152 340 197 376, à peu de choses près égale à la probabilité d'acheter consécutivement 4 billets de loterie et de gagner le gros lot à chaque fois. Dans le cas du texte entier de Hamlet, les probabilités sont tellement négligeables qu’elles sont difficilement représentables pour un homme. Le texte de Hamlet, même dépouillé de toute ponctuation, contient bien plus de 130 000 lettres.

Gian-Carlo Rota écrivit dans un manuel de probabilité (inachevé lorsqu’il mourut) :

« Si le singe pouvait taper sur son clavier une touche par nanoseconde, alors la durée d'attente pour que le singe dactylographie complètement Hamlet serait si longue que l’âge estimé de l’univers paraîtrait insignifiant par comparaison… et ce n'est pas une bonne méthode pour écrire les pièces de théâtre. »

En physique, la force de l' « argument de singes » ne se situe pas dans la probabilité pour que les singes produisent éventuellement quelque chose d’intelligible, mais dans la réalité pratique qu'ils ne le feront jamais (et que même s'ils en faisaient une partie, il serait impossible de l'identifier comme telle). N'importe quel processus physique moins probable que la réussite de tels singes, est dans le cours d'une vie humaine, et parfois même relativement à l'âge de l'univers, impossible ; c'est là une base statistique liée au second principe de la thermodynamique.

RFC 2795

La RFC 2795, en date du 1^er avril 2000, établit un protocole, IMPS, permettant de coordonner une infinité de singes savants au cas où l'on désirerait essayer tout de même^[1].

Le mythe du singe savant

Certains Américains prétendent, bien que ce soit fortement improbable, que l'utilisation par Borel des singes et des machines à écrire dans son théorème fut inspirée d’une argumentation de Thomas Henry Huxley le 30 juin 1860. Huxley en aurait parlé au cours d'une discussion avec l'évêque anglican d'Oxford, Samuel Wilberforce, tenue lors d'une réunion de l’association britannique pour l'avancement de la Science à Oxford, de laquelle Wilberforce était vice-président, ce dernier ayant été ébloui par la publication de Charles Darwin sur l'Origine des espèces sept mois plus tôt, en novembre 1859.

Aucune transcription de la discussion n'existe, personne actuellement ne peut en témoigner, et aucun mémoire de Huxley n'inclut une quelconque référence au théorème du singe savant.

Certains supposent que ce rapprochement hypothétique de la discussion avec le théorème du singe savant est probablement un mythe urbain dont l’origine provient du fait que cette discussion ait dégénéré en parlant des singes : l'évêque demanda si Huxley descendait d'un singe du côté de sa grand-mère ou de son grand-père, et Huxley répondit qu'il descendait plutôt d'un singe que de quelqu'un comme l’évêque qui argue avec une telle mauvaise foi. Il est encore moins probable qu’Huxley ait fait allusion à une machine à écrire. Bien que des brevets pour les machines à écrire modernes aient été accordés à partir de 1714, la production commerciale des machines à écrire n'a commencé qu’en 1870, et un orateur aussi habile qu’Huxley n’aurait certainement pas laissé dépendre son argumentation d’une machine dont l'existence était encore inconnue de la majeure partie de son auditoire.

Littérature et culture populaire

Dans les Voyages de Gulliver (1721), Jonathan Swift anticipe l’idée principale du théorème, dépeignant un professeur de la grande académie de Lagado qui essaye de créer une liste complète de toutes les connaissances scientifiques en faisant générer en permanence par ses étudiants des chaînes de lettres aléatoires en tournant des manivelles sur un mécanisme (partie trois, chapitre cinq).

Un thème semblable est traité dans La Bibliothèque de Babel de Jorge Luis Borges, dans laquelle se trouve un nombre illimité de volumes remplis de chaînes de caractères aléatoires. Toutes les grandes œuvres de la littérature sont présentes par construction dans la bibliothèque, ainsi que la biographie à venir de celui qui errerait à la recherche de son avenir dans l'immense bibliothèque; mais de telles œuvres sont dépassées en nombre par des travaux médiocres, à leur tour écrasés par une masse énormes de livres dont le contenu n'a pas le moindre sens. Richard Dawkins a pour sa part imaginé le portable de Babel, un ordinateur portable dont les 4 mégaoctets de mémoire seraient remplis aléatoirement. Là encore, tous les noyaux de Windows comme de Linux, passés, présents ou futurs (jusqu'à 4 Mo du moins) seraient quelque part.

Borges reprend également cette idée dans sa nouvelle l'immortel (du recueil l'Aleph), en supposant qu'Homère ait été immortel et donc sans mérite car « aussitôt accordé un délai infini, avec des circonstances et des changements infinis, l'impossible aurait été de ne pas composer, au moins une fois, l'Odyssée »^[2].

Les références de culture populaire à ce théorème incluent :

• Les Simpson : dans un épisode, Charles Montgomery Burns a dans sa propre chambre 1000 singes devant des machines à écrire, dont un est châtié pour avoir fait une faute sur un mot de la première phrase du livre Le Conte de deux cités (A Tale of Two Cities) « It was the best of times, it was the blurst of times. »), (au lieu de « It was the best of times, it was the worst of times » ce qui signifie « c’était le meilleur des temps, c'était le pire des temps ») ;
• Les Griffin (Family Guy) : un groupe de singes est montré en train de travailler sur un vers de Roméo et Juliette de Shakespeare dans une scène intermédiaire ;
• le Guide du voyageur galactique (Ford Prefect et Arthur Dent, sous l’influence du trajet de l’infinie improbabilité, sont pris en embuscade par un nombre infini de singes qui leurs demandent un avis sur leur manuscrit d’Hamlet) ;
• dans la bande dessinée Dilbert, Dogbert indique à Dilbert que son poème prendrait « trois singes et dix minutes » (sachant qu'il faut selon Dogbert 1000 singes et un temps infini pour écrire toutes les œuvres de Shakespeare).
• l'Histoire sans fin de Michael Ende : le héros Bastien Balthasar Bux se retrouve dans la ville des anciens empereurs, où des fous jouent au jeu des probabilités. Le singe Argax lui explique le fonctionnement : quantité de dés dont chaque face est recouverte d'une lettre jonchent le sol. Les fous, encouragés par Argax, les disposent au hasard devant eux car ils ont perdu la parole. Le singe explique que parfois certains mots apparaissent, et que si l'on continue à jouer cent ans, mille ans, un poème doit apparaître de temps en temps. Et que si on y joue éternellement, toutes les histoires possibles doivent sortir, y compris celle-là.

Le théorème est aussi à la base d’une pièce en un seul acte de David Ives intitulée « Words, Words, Words » (« Mots, Mots, Mots »), qui apparaît dans sa collection All in the Timing. Dans cette pièce, trois singes appelés Milton, Swift, et Kafka ont été confinés dans une cage par un scientifique jusqu’à ce qu’ils écrivent Hamlet. Il y a une courte histoire humoristique de R.A. Lafferty intitulée « Been a Long, Long Time » signifiant « longtemps, longtemps », dans laquelle un ange est puni et doit corriger tous les textes produits jusqu’à une date ultérieure (après que des trillions d’univers meurent), quand des singes auront réussi à fournir une copie parfaite des travaux de Shakespeare.

Dans la pièce Rosencrantz & Guildenstern are Dead de Tom Stoppard, un personnage dit, « si un million de singes… » mais ne continue pas sa phrase et change de sujet. Il s’agit certainement d’une allusion humoristique, puisque les personnages sont censés jouer dans Hamlet.

En 2000, le comité de normalisation de standard pour internet IETF, à l’occasion d’un April 1st RFC a proposé «une suite de protocole d’une infinité de singes (IMPS)», une méthode pour diriger par internet une ferme contenant une infinité de singes.

Dans la page personnelle (blog) de l'auteur et acteur Wil Wheaton, figure le slogan, « 50 000 singes devant 50 000 machines à écrire ne peuvent pas se tromper ». Ce mot d’esprit a remporté un prix de Blog award en 2002 dans la catégorie « meilleur sous-titre de Weblog ».

Robert Wilensky remarqua une fois avec amusement que « nous avons tous entendu parler qu’un million de singes frappant sur un million de machines à écrire reproduiront tôt ou tard les travaux entiers de Shakespeare. Maintenant, grâce à l’internet, nous savons que ce n'est pas vrai  ».

Le comédien Bob Newhart avait un rôle dans une comédie, de technicien de laboratoire chargé de la surveillance d’une expérimentation sur un « très grand nombre de singes » et dans ce rôle il découvrit que l’un des singes avait dactylographié « être, ou ne pas être; c'est la gezortenblatt ». En allemand « gezortenblatt » pourrait signifier « une question de braillement ».

Les chèvres, une bande dessinée sur internet illustrée par Jonathan Rosenberg, raconte une histoire appelée les machines à écrire infinies où plusieurs personnages sont déplacés accidentellement dans une autre dimension. Ils constatent que cette dimension est peuplée par des singes avec des machines à écrire, censés dactylographier les manuscrits appartenant à de multiples autres dimensions.

La Désencyclopedie, parodie de Wikipédia, prétend sur sa page d'accueil être entièrement écrite par des singes savants. Il y est d'usage de faire référence aux utilisateurs par le terme Singes savants.

Dans le 7ème épisode des Lone Gunmen (La Planète des Frohikes), des singes tapent sur des machines à écrire et Simon écrit le texte de Shakespear dicté.

Singes de laboratoire

Il s’agit d’une expérience de pensée qui, clairement, ne peut pas être effectuée dans la réalité, puisqu'elle demanderait un temps infini ou une infinité de singes. Néanmoins, elle a inspiré de nombreux travaux dans la génération aléatoire finie de textes.

Le site « le simulateur de singe shakespearien », commencé le 1^er juillet 2003, contient une appliquette qui simule une grande population de singes dactylographiant aléatoirement, dans l'intention de voir combien de temps il faut à ces singes virtuels pour produire une pièce complète de Shakespeare du début jusqu'à la fin. Le 3 janvier 2005, le programme a obtenu 24 lettres consécutives, quatre mots ont été enregistrés (« RUMOUR. Open your ears; 9r"5j5&?OWTY Z0d "B-nEoF.vjSqj[...» de Henry VI, part 2). À cause des limitations de capacité de traitement, le programme emploie un modèle probabiliste (en employant un générateur de nombres aléatoires) au lieu de réellement produire aléatoirement du texte et de le comparer à Shakespeare. Quand le simulateur « détecte une coïncidence » (c'est-à-dire, quand le générateur de nombres aléatoires produit une certaine valeur), le simulateur réagit à la coïncidence en produisant du texte assorti.

En 2003, des scientifiques de l’université de Plymouth, auraient effectué une expérience avec des singes au zoo de Paignton à Devon en Angleterre : laisser pendant un mois un clavier d'ordinateur dans la clôture qui parquait six macaques à crête de Sulawesi. À la fin ils constatèrent que les singes n'avaient produit que cinq pages ne contenant que quelques lettres longuement répétées, et ils rapportèrent que les singes avaient commencé par attaquer le clavier avec une pierre, et avaient ensuite uriné et déféqué dessus (voir aussi Prix Ig Nobel).

La levée du « paradoxe »

Une question peut à ce stade subsister dans l'esprit : peut-on réellement produire des œuvres littéraires avec ce système ? Il est clair qu'on ne fait que remplacer un problème par un autre plus grand : au lieu de composer une œuvre, il faut lire et tester des milliards de milliards de documents et arriver à déterminer lequel contient l'œuvre. La quantité d'information consommée dans le processus sera au moins aussi grande, et en ce sens ce paradoxe n'est pas dénué de similitude avec celui du démon de Maxwell, dont la physique crut quelques mois pouvoir espérer des miracles aussi.

Exprimé en termes plus simples, cela signifie que la complexité de retrouver une œuvre donnée de Shakespeare dans la bibliothèque de Babel sera très exactement la même que celle de recopier directement cette pièce à la main : la bibliothèque de Babel (ou le travail des singes) ne contient paradoxalement pas d'information. Ou, ce qui revient au même, c'est le contexte lié au vécu du récepteur, et lui seul, qui fait que tel « bruit » particulier devient pour lui une « information » (parce qu'il connaît la grammaire d'une langue, possède un vocabulaire et dispose d'un vécu lui permettant de conférer du sens à une suite de caractères qui en soi ne se distingue pas des autres (voir aussi Théorie d'Everett).

Paul Valéry avait exprimé une réserve similaire dans L'homme et la coquille (Variété III) : « le chiffre qui sort à la loterie ne peut avoir de sens pour moi, ne se distingue de tous les autres, que si je possède un billet qui le porte .»

Et en mathématiques ?

On pourrait imaginer de gagner du temps dans le processus en ne produisant que des phrases bien formées. Cela est difficile pour une langue naturelle, mais facile en mathématiques, dans le cadre de la logique mathématique. On envisagea donc lors des premiers développements du calcul formel sur ordinateur de fournir des axiomes et des règles de déduction à une machine, le mathématicien n'ayant plus qu'à examiner chaque jour les listings et à publier les théorèmes du jour. Il va de soi que le problème est le même à une seule chose près : toutes les formules imprimées seront cette fois correctes, c’est-à-dire bien formées et de plus vraies (et fournies avec la démonstration).

En revanche, le problème du dépouillement de papier reste inchangé. De plus, au cours d'une conférence sur les fondements des mathématiques, Jean-Yves Girard fait la remarque suivante (selon lui, la logique formelle ressemble plus à un travail de bureaucrate qu'à un travail de singe savant) :

« La question qui se pose est la suivante : est-ce que les mathématiques sont une activité formelle ? Est-ce que les mathématiques sont une activité "bureaucratique" ? Est-ce qu'on aurait pu confier le théorème de Fermat à un groupe d'énarques ? Ils y seraient arrivés en 300 ans ? Bon c'est impossible parce qu'il faut des idées. »

Il faut en effet l'idée du théorème, aussi importante au moins que sa démonstration. Une machine peut fabriquer "au kilomètre" des énoncés mathématiquement tous vrais accompagnés de leur démonstration établie par ses soins. Néanmoins, dans ces millions d'énoncés, le fait d'en distinguer quelques uns pour en faire - et d'eux seuls - des théorèmes relève d'un vécu du mathématicien, qui aura reconnu un lien possible et éventuellement fécond avec des travaux d'autres branches du savoir comme la physique, la statistique, la biologie, etc. Les théorèmes spécifiques de Thalès et de Pythagore, par exemple, étaient liés à des besoins latents concernant l'architecture ou l'établissement d'un cadastre.

• Voir aussi : Épistémologie

Art informatique

Selon ce même principe, des formes ^[3] (pseudo)aléatoires ont été utilisées pour créer de l'art abstrait. Le logiciel suit des structures types, pré-programmées. L'utilisateur humain peut pondérer ces structures en fonction de ses préférences, pour faire composer des dessins ou de la musique qui lui plaise.

Lien avec la philosophie

Une question importante de la philosophie est "Pourquoi y a-t-il quelque chose plutôt que rien ?". Dans la mesure où la réalisation de tous les possibles équivaut à une absence totale d'information, une boutade classique de physiciens consiste à dire qu'il se peut tout simplement que nous ne soyons que l'une des formes possibles du "rien".

(Une sorte d'anti-hasard existe ici : nous ne pouvons en tant qu'observateurs exister que dans un des univers particuliers susceptibles de donner naissance à des observateurs. Il s'agit du principe anthropique)

Nombres-univers

On peut dans certains cas évaluer si la suite des décimales d'un nombre irrationnel possède des caractéristiques statistiques analogues à une suite de chiffres aléatoires. Lorsque tel est le cas, on peut attendre de cette suite les mêmes caractéristiques qu'un texte frappé par un singe (non) savant : en poussant son investigation assez loin dans cette suite, on peut espérer y découvrir son numéro de téléphone, sa date de naissance, notre numéro de sécurité sociale la dernière suite gagnante des numéros du Loto et avec une convention pour associer des lettres et signes typographiques aux couples de chiffres, son nom de famille, son adresse, et en étant très opiniâtre - La Cigale et la fourmi, Le Corbeau et le Renard et La Bibliothèque de Babel, de Jorge Luis Borgès. Il n'est donc pas davantage possible d'utiliser le procédé pour la moindre création littéraire, sauf à la rigueur pour un exercice de style (Jean-Pierre Petit par exemple a utilisé des mots créés par combinaisons aléatoires de préfixes et suffixes dans ses bandes dessinées).

Notes

Références

• (en) Aucun mot pour décrire la pièce de théâtre des singes (9 mai 2003) BBC News
• (en) Preuve que la théorie des singes est fausse (9 mai 2003) CBS News
• (en) RFC 2795 — The Infinite Monkey Protocol Suite (IMPS)

Liens internes

• Nombre normal
• La Bibliothèque de Babel Une nouvelle traitant du même thème

Liens externes

• Parodie réelle du concept du clavier/singe
• Les singes n'écrivent pas du Shakespeare

• Portail des mathématiques