Octet

Pour les articles homonymes, voir Octet (homonymie).

 Ne doit pas être confondu avec byte.

Pourcentage de différence entre la réprésentation métrique et la représentation binaire.

L’octet est une unité de mesure en informatique mesurant la quantité de données. Un octet est lui-même composé de 8 bits, soit 8 chiffres binaires. Le byte, qui est un ensemble de bits adjacents, a presque toujours une taille d'un octet et les deux mots sont généralement, mais abusivement, considérés comme synonymes^[1].

Symboles

Le symbole de l’octet est la lettre « o » minuscule.

La lettre « O » (en majuscule), n'est pas acceptable dans le système international d'unités (SI) à cause du risque de confusion avec le chiffre 0 et que les lettres majuscules sont réservées aux mesures liées à une personne. Cependant, cette question n’est pas tranchée, les unités d’information ne faisant pas partie du SI.

Multiples

Traditionnellement, lorsqu'ils sont appliqués aux octets, les préfixes « kilo », « méga », « giga », etc. ne représentent pas une puissance de 10 (10³ = 1 000), mais une puissance de 2 (2¹⁰ = 1 024) (plus précisément, il s'agit de puissance de 10³ et 2¹⁰, car la notion de multiple porte sur l'exposant 3 ou 10). Cependant cette tradition viole les normes en vigueur pour les autres unités, y compris le bit, et n'est même pas appliquée uniformément aux octets, notamment dans la mesure de la capacité des disques durs. Une nouvelle norme a donc été créée pour noter les multiples de 2¹⁰ = 1 024 : les « kibi », « mébi », « gibi », etc.

Ubuntu écrit les valeurs en Gio (puissance de 2), ce qui est conforme au SI.

L'usage traditionnel reste largement en vigueur chez les professionnels comme le grand public, même si c'est en contradiction avec les recommandations SI qui définissent clairement d'autres préfixes. L'usage des préfixes binaires reste très confidentiel et ne se répand presque pas dans le langage courant, alors que les valeurs représentées par ces unités en puissance de 2 sont très utilisées dans les applications, notamment les systèmes d'exploitation. Cependant, leur utilisation commence à se répandre, notamment dans le monde du logiciel open source, comme dans les systèmes d'exploitation libre de type GNU/Linux.

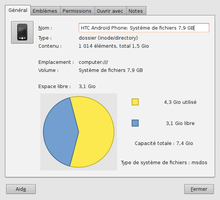
Windows Vista écrit les valeurs en Go (puissance de 10), tout en les calculant en Gio (puissance de 2), ce qui est contraire à l'écriture dans le SI.

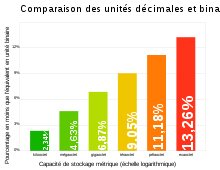
Cette distinction est d'ailleurs utilisée depuis longtemps par les fabricants de disques durs. Le fait que l'usage de préfixes en puissances de 10 permette d'afficher commercialement des capacités supérieures à celles données par les puissances de 2 peut introduire une erreur d'appréciation de la part d'utilisateurs non avertis. Ainsi, un disque dur de 100 gigaoctets (100×10⁹ octets) contient le même nombre (à l'erreur d'arrondi près) d'octets qu'un disque de 93,13 gibioctets (93,13×2³⁰ octets).

La très grande majorité des disques durs étant divisés et adressables en secteurs de 512 octets, un comptage en unités de 1 024 octets serait plus naturel (en utilisant cette fois les préfixes binaires) ; les disques de stockage à mémoire non volatile (y compris les clés USB, lecteurs MP3 mobiles, etc.) utilisent généralement l'unité avec le préfixe binaire. Mais cette capacité est celle du volume non formaté, le formatage des disques en système de fichiers en retire une partie, de plus une petite partie du volume de la mémoire non volatile est parfois utilisé par le logiciel interne de l'unité de stockage.

D'autres usages courants, mais incorrects, suppriment complètement le nom ou le symbole de l'unité pour ne plus garder que le nom ou le symbole du préfixe multiplicateur « k ». Cela entraîne cependant de nombreuses ambigüités quant à la nature de cette unité, notamment quand on l'utilise pour exprimer un taux de transfert de données ou la capacité d'une puce de mémoire. En effet, dans ces deux cas, il est courant que l'on mesure en bits plutôt qu'en octets.

Multiples normalisés

La normalisation des préfixes binaires de 1998 par la Commission électrotechnique internationale spécifie les préfixes suivants pour représenter les puissances de 2 :

• kibi pour « kilo binaire » ;
• mébi pour « méga binaire » ;
• gibi pour « giga binaire » ;
• tébi pour « téra binaire » ;

et ainsi de suite.

Concernant les multiples de l'octet, cela donne^[2] :

Les préfixes kilo, méga, giga, téra, etc., correspondent aux mêmes multiplicateurs que dans tous les autres domaines : des puissances de 10. Appliqué à l'informatique, cela donne :

Multiples traditionnels

De manière erronée selon le SI, avant la normalisation de 1998, et encore de nos jours dans l'usage courant, on utilise les unités dérivées que sont le kilo-octet, le méga-octet, le giga-octet, etc. pour représenter les valeurs suivantes en puissance de 2 :

Variantes orthographiques

La langue française pose aussi un problème de syntaxe, relative à la prononciation de la voyelle initiale du mot octet avec un préfixe ; aussi, voit-on dans la littérature les formes suivantes : « kilo-octet » (avec trait d'union), « kilooctet » (sans trait d'union) ou « kiloctet » (fusion des voyelles). Dans les unités SI, le nom du préfixe s'écrit toujours sans trait d'union avant le nom de l'unité de base, le kiloctet devrait donc être la norme mais sa prononciation semble peu claire.

Propriétés

Propriétés de représentation binaire

Un octet peut représenter 2⁸ = 256 valeurs différentes. La valeur de tout octet peut s'écrire avec un entier naturel entre 0 et 255 compris (en base 10). Elle peut aussi s'écrire avec huit chiffres binaires, entre 00000000₂ et 11111111₂ compris, ou avec deux chiffres hexadécimaux, entre 00₁₆ et FF₁₆ compris. La notation hexadécimale est utilisable dans de nombreux langages informatiques car elle est pratique et compacte pour noter la valeur d'un, ou plusieurs, octet(s).

Un octet peut servir à noter un entier naturel, appelé en informatique « non signé », entre 0 et 255 (en base 10). Une autre convention courante, le complément à deux, permet de noter un nombre entier, ou « signé », entre -128 et +127 compris (en base 10). Voir aussi l'article Système binaire.

De nombreuses conventions existent pour représenter un caractère par un ou plusieurs octets. On peut notamment citer le codage ISO 8859-1 très utilisé pour représenter avec un octet les 26 lettres minuscules, les 26 majuscules, les 10 chiffres, les lettres accentuées et la ponctuation, des langues d'Europe occidentale, dont le français. Plus récent, le codage UTF-8 permet de noter tout caractère avec un à quatre octets, selon le caractère. L'article sur le codage de caractères développe ce thème.

Propriétés de représentation décimale

Dans certaines applications nécessitant un codage exact des valeurs décimales (par exemple pour les applications financières), les puissances de 2 peuvent ne pas s'avérer pratiques. Aussi un octet est parfois utilisé pour stocker jusqu'à 2 chiffres décimaux exactement (entre 00₁₀ et 99₁₀), chacun codé sur un quartet (4 bits) distinct entre 0000₂ = 0₁₀ et 1001₂ = 9₁₀. Les autres valeurs de quartets peuvent être utilisées pour coder la position d'une virgule décimale, un signe, l'absence de chiffre significatif à la position indiquée, ou une autre fonction spéciale (valeur infinie, valeur erronée non numérique, etc.). Certains calculateurs (et des bibliothèques logicielles de calcul à virgule fixe ou travaillant sur de très grands entiers ou des valeurs de grande précision) utilisent ce format dit « BCD », sigle anglais de binary coded decimal (décimal codé en binaire).

L'usage du codage BCD était populaire sur les anciens systèmes (notamment ceux utilisant l'EBCDIC) car cela évitait une conversion finale coûteuse pour afficher les nombres à virgule flottante. De plus ce système était plus pratique au temps où les données étaient entrées manuellement sur des cartes perforées : pour convertir un nombre BCD en caractères, il suffisait d'éclater le nombre BCD en deux en n'utilisant qu'un seul quartet par octet pour représenter le chiffre en décimal, le quartet de poids fort prenant une valeur fixe indiquant simplement que c'est un chiffre décimal. Les autres valeurs de quartets de poids fort étaient utilisées pour indiquer que c'était une lettre majuscule, une lettre minuscule ou un autre symbole ou ponctuation. Aujourd'hui, dans la plupart des systèmes actuels, le codage EBCDIC des caractères et du BCD pour les valeurs numériques est plus rarement utilisé car la plupart des calculs se font plus rapidement en représentation binaire de façon matérielle avec une précision globale prédéfinie (codée sur un nombre fixe d'octets).

Il existe des variantes du système BCD permettant de conserver une représentation précise des nombres à virgule fixe ou flottante en base 10, tout en permettant une plus grande compacité de stockage et en rendant les calculs plus rapides. L'astuce consiste à grouper les chiffres décimaux et les représenter en binaire sur un groupe de plusieurs octets. Par exemple :

• tout d'abord la représentation en quartets s'avère coûteuse en termes de traitement, et une valeur BCD est généralement d'abord convertie en supprimant la séparation en quartets, pour alors représenter en binaire les deux chiffres décimaux sur le même octet ; le calcul est alors simplifié car il s'effectue par groupe de 2 chiffres à la fois au lieu d'un seul ; cette représentation laisse 1 bit de poids fort inutilisé (mais on peut l'utiliser comme marqueur pour des valeurs spéciales) ;
• on peut représenter exactement 4 chiffres décimaux dans un groupe de 2 octets (c'est-à-dire sur 16 bits, puisque ceux-ci peuvent contenir 2¹⁶ = 65 536 valeurs différentes) ; avec une représentation BCD, on stockerait exactement également 4 chiffres décimaux, mais les calculs se feraient uniquement chiffre par chiffre^[3] (c’est-à-dire 4 fois plus lentement) ; cette représentation laisse 2 bits de poids fort inutilisés (mais on peut les utiliser comme marqueurs pour des valeurs spéciales) ;
• on peut représenter exactement 7 chiffres décimaux dans un groupe de 3 octets (c'est-à-dire sur 24 bits, puisque ceux-ci peuvent contenir 2²⁴ = 16 777 216 valeurs différentes) ; avec une représentation BCD, on ne stockerait exactement que 6 chiffres décimaux ; cette représentation ne laisse aucun bit inutilisé ;
• on peut représenter exactement 9 chiffres décimaux dans un groupe de 4 octets (c'est-à-dire sur 32 bits, puisque ceux-ci peuvent contenir 2³² = 4 294 967 296 valeurs différentes) ; avec une représentation BCD, on ne stockerait exactement que 8 chiffres décimaux ; cette représentation laisse 2 bits de poids fort inutilisés (mais on peut les utiliser comme marqueurs pour des valeurs spéciales). Cette représentation est souvent utilisée dans les bibliothèques mathématiques de calcul sur des nombres de très grande précision.

Usages

Les processeurs n'opèrent généralement pas sur chaque bit individuellement, mais sur des groupes de bits. L'habitude de concevoir le matériel pour qu'il traite les bits par huit, ou par multiples de huit, s'est généralisée depuis les années 1970, si bien qu'aujourd'hui l'octet et ses multiples sont généralement utilisés comme mesure de la capacité de mémorisation des mémoires informatiques : mémoire vive, disquette, disque dur, CD-ROM, etc. La taille des fichiers est aussi mesurée en octets (avec le plus souvent les multiples conventionnels, sauf pour les disques durs ; voir ci-dessous).

Le taux de transfert des bus informatiques entre les applications informatiques et périphériques informatiques locaux est généralement donné en octets par seconde (avec les multiples normalisés ; voir ci-dessous). Mais les débits sur les réseaux ou supports de transmission de données s'expriment plutôt :

• soit en bauds (avec les multiples normalisés), c’est-à-dire le nombre de symboles codés par seconde, pour les technologies matérielles de modulation de très bas niveau, par exemple dans les modems, ces technologies séparant la fréquence d'échantillonnage en bauds (fortement liée à la bande passante physique exprimée en hertz) de la précision d'échantillonnage exprimée en bits par symbole (fortement liée au rapport signal/bruit du support de transmission exprimé en décibels ou en bits),
• soit en bits par seconde (avec les multiples normalisés), pour le débit binaire final utilisable, résultant du produit du débit en bauds par le nombre de symboles codés utilisables par symbole, diminué éventuellement des bits de détection ou correction d'erreurs ou de synchronisation.

Bits et octets

Exemples de conversion des bits vers octets (sans normalisation SI) :

• 8 bits = 1 octet
• 1 kilobit = 1 024 bits = 128 octets
• 512 kilobits = 524 288 bits = 65 536 octets = 64 kilo-octets (65 536/1 024).
• 1 mégabit = 1 048 576 bits = 131 072 octets = 128 kilo-octets (131 072/1 024).
• 10 mégabits = 10 485 760 bits = 1 310 720 octets = 1,25 méga-octets (1 310 720/1 024²).
• 100 mégabits = 104 857 600 bits = 13 107 200 octets = 12,5 méga-octets. (13 107 200/1 024²).

Mots

Lorsque le traitement se fait sur plusieurs octets simultanément, notamment 2 octets (16 bits) et 4 octets (32 bits), on parle parfois de mot et de double-mot. La signification de ces termes a tendance à varier avec le contexte, notamment car en terminologie des langages d'assemblage pour processeurs, le « mot » désigne souvent la quantité d'information dans un registre de calcul entier pour une opération élémentaire, cette quantité pouvant aussi dépendre du mode d'adressage utilisé par le processeur à l'exécution, (ou des traditions de programmation pour un système d'exploitation donné), aussi n'est-il pas recommandé de les utiliser.

Les termes doublet (16 bits), quadlet (32 bits) et octlet (64 bits) sont parfois utilisés alors pour enlever toute ambigüité.

Octets, bits et décibels

Le bit (ou son multiple l'octet) est une unité dérivée parfois plus pratique dans certains calculs sur les signaux que le bel noté « B » ou le décibel noté « dB » : une qualité de signal de 1 bit est définie comme le double du logarithme binaire d'un rapport signal/bruit exactement égal à 2 et le bel est défini comme le logarithme décimal d'un rapport de grandeurs exactement égal à 10.

Par la suite, on parle de signaux de qualité 1 octet :

• La qualité de signal de 1 bit vaut exactement 2.log₁₀(2) bels ou 20.log₁₀(2) décibels (soit environ 0,6 B ou 6 dB).
• La qualité de signal de 1 octet vaut exactement 8 fois plus, soit 16.log₁₀(2) bels ou 160.log₁₀(2) décibels (soit environ 4,8 B ou 48 dB).

On peut noter qu'en dessous de 6 dB de rapport signal/bruit, il n'est théoriquement plus possible de détecter un seul bit entier d'information avec un seul échantillon. Cependant, la détection d'informations (pour la transmission ou le stockage) dans un tel signal est possible grâce à la technique du suréchantillonnage. Il suffit de prendre plusieurs échantillons : les rapports signal/bruit de chaque échantillon s'additionnent alors jusqu'à dépasser le seuil de 6 dB, au-delà duquel il est possible, par calcul, de détecter, transmettre ou stocker 1 bit d'information. On fait alors de même avec des signaux en dessous de 48 dB pour détecter, transmettre ou stocker, par calcul, 1 octet d'information. Les plus petits « fragments » de bits ou d’octets sont donc utilisables.

Sur les supports de transmission de données

Débit de transmission

Le débit maximum d'un support de transmission de données (exprimé en décibels par seconde, ou respectivement bits par seconde, ou octets par seconde) est la somme des produits de la fréquence d'échantillonnage de chaque signal transporté (exprimée en hertz) par la qualité de ce signal (exprimée en décibels, ou respectivement bits ou en octets). Selon les technologies employées, il existe toujours un compromis entre qualité et fréquence d'échantillonnage de chaque signal, le meilleur compromis (qui apporte le débit maximum) étant obtenu quand le produit qualité-fréquence est maximum.

Le débit (ou capacité temporelle d'informations) effectif d'un support de transmission de données (exprimé en décibels par seconde, ou respectivement en bits par seconde ou en octets par seconde) est toujours strictement inférieure à ce débit maximum théorique qu'il est impossible de dépasser sur le même support (à condition d'avoir pris en compte tous les signaux détectables sur ce support).

L’unité la plus employée pour mesurer le débit d’un support de transmission de données est le bit par seconde (et ses multiples normalisés en puissances de 10 comme le kilobit par seconde symbolisé kbit/s, voire kbps en anglais) pour les supports physiques, mais l’usage de l’octet par seconde (et de ses multiples normalisés en puissances de 10, ou traditionnels en puissances de 2) est très courant pour les applications et protocoles de transfert de fichiers.

Quantité d'informations transmise

La quantité d'informations maximale transmise dans un intervalle de temps sur un support de transmission de données est l'intégration de son débit sur chaque position temporelle dans cet intervalle où les échantillons sont transmis.

La quantité d'informations effectivement transmise est toujours strictement inférieure à cette quantité maximale théorique. Elle se mesure en décibels, ou respectivement en bits ou en octets (ou ses multiples normalisés en puissances de 10, ou conventionnels en puissances de 2). L'unité la plus utilisée est le kilooctet traditionnel, symbolisé ko en français.

Sur les supports de stockage d'informations

Capacité par unité spatiale

On effectue le même raisonnement pour la capacité des supports statiques de stockage, en considérant que chaque position de la longueur (ou respectivement de la surface ou du volume) de ce support définit un certain nombre de signaux ayant chacun une qualité exprimée en bits, octets ou décibels, la nature de ces signaux détectables dépendant des capteurs employés (conversion de signaux électriques en signaux magnétiques, optique…), de leur qualité (c'est-à-dire leur précision intrinsèque), et du niveau de bruit environnant (dépendant aussi de la construction du support, notamment son isolation).

Le domaine spatial de stockage le plus utilisé aujourd'hui est la surface (disquettes, disques durs, optiques, magnéto-optiques, mémoires électroniques…), mais la longueur est encore utilisée (bandes magnétiques). Le domaine spatial du volume est encore à l'état expérimental (stockage optique dans un cristal, holographique…), mais commence à apparaître sur les disques optiques multicouche (les unités correspondantes restent encore surfaciques).

On peut alors parler de capacité linéaire (ou respectivement surfacique ou volumique) d'informations exprimée en décibels par mm (ou respectivement par mm² ou par mm³) ou donc aussi en bits par mm (ou respectivement par mm² ou par mm³) ou encore en octets par mm (ou respectivement par mm² ou par mm³), l'unité de longueur (ou respectivement de surface ou de volume) remplaçant la seconde dans le paragraphe précédent, et selon les mêmes formules de Nyquist-Shannon pour la qualité des signaux échantillonnés sur ce support. Pour les disques durs, disques optiques ou magnéto-optiques, l'unité de capacité surfacique la plus utilisée est le bit par mm², ou ses multiples normalisés en puissances de 10 comme le kilobit par mm², symbolisé kb/mm².

On trouve cependant aussi mention du multiple normalisé kilooctet par mm² (ko/mm² en français). Les unités traditionnelles ne sont jamais employées à ce niveau, au contraire des fabricants de mémoires qui préfèrent les unités traditionnelles en puissances de 2 comme le kilooctet par mm² (qui parfois comptent plutôt en nombre de transistors par unité de surface, mais cette fois avec les multiples conventionnels en puissances de 10, sachant qu'un bit d'information stockée nécessite souvent deux transistors).

Capacité totale du support

La capacité totale d'informations maximale de ce support, exprimée en décibels, bits ou octets est l'intégration de cette capacité linéaire (ou respectivement surfacique ou volumique) sur chaque position de la longueur (ou respectivement de la surface ou du volume) de ce support.

La capacité totale d'informations effective d'un support de stockage se mesure le plus souvent en octets (ou ses multiples normalisés en puissances de 10, comme le kilooctet, symbolisé conventionnellement ko sur les disques durs). Mais le plus souvent l'interface de ce support se fait par secteurs de taille conventionnelle de 512 octets, et donc la capacité d'utilisation de ce support dans les systèmes d'exploitation se mesure plus souvent et de façon plus pratique avec les multiples traditionnels.

Notes et références

Voir aussi

• Système binaire
• Préfixe binaire
• Format de données
• Boutisme, organisation des octets
• Mémoire cache

• Portail de l’informatique