Quadrilatère (mathématiques élémentaires)

QUADRILATÈRES
┌─────────────┼─────────────┐
concave		convexe		croisé
┌─────────────┼─────────────┐
à cercle circonscrit		trapèze		tangentiel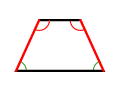
| ┌───────────┤				|
trapèze isocèle diagonales égales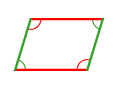		parallélogramme centre de symétrie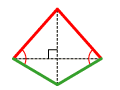		cerf-volant diagonales perpendiculaires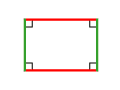
└─────┬─────┘			└─────┬─────┘
rectangle angles droits			losange côtés égaux
└──────────┬─────────┘
carré

En géométrie plane, un quadrilatère (du latin quatuor, quatre et latus, lateris, côté) est un polygone à quatre côtés.

Le mot équivalent d'origine grecque est tétragone (de τετρα / tetra, quatre et πλευρα / gonia, angle) ou « tétragone » (de γονοσ / gonos, angle). Le mot tétragone était employé par Gerbert d'Aurillac au X^e siècle et par Oresme au XIV^e siècle. Le terme quadrilatère est introduit en 1554 par Peletier. Certains auteurs latins employaient le mot « quadrangle » (Alcuin, VIIIe siècle) ou « helmuariphe », terme d'origine arabe (Campanus, XIII^e siècle, et d'autres à la Renaissance). Pour les Grecs, un quadrilatère avec un angle rentrant s'appelait un « koïlogone » (de κοιλοσ / koïlos, creux), et certains appelaient « trapèze » un quadrilatère dont tous les côtés sont inégaux. « Tétragone » est employé par Euclide dans Les Eléments pour désigner le carré^[1].

Trapèze, parallélogramme, losange, rectangle, carré et cerf-volant sont des quadrilatères particuliers.

Sommaire 1 Caractéristiques 2 Quadrangle et quadrilatère 3 Notation 4 Typologie des quadrilatères 4.1 Classements 5 Propriétés générales des quadrilatères convexes 6 Liens connexes 7 Références

Caractéristiques

Un quadrilatère est la figure notée « ABCD » formée par :

• quatre points A, B, C et D : les sommets du quadrilatère ;
• quatre segments [AB], [BC], [CD] et [DA] : les côtés du quadrilatère.

Les sommets A et C sont dits opposés ; ainsi que les sommets B et D.
Les diagonales [AC] et [BD] joignent les sommets opposés.

Un quadrilatère peut être :

• convexe, si les deux diagonales sont à l'intérieur du quadrilatère,
• concave, si (au moins) une des diagonales est à l'extérieur du quadrilatère,
• croisé, si les deux diagonales sont à l'extérieur du quadrilatère. Un quadrilatère croisé est concave.

La formule de Brahmagupta donne l'aire d'un quadrilatère convexe dont les sommets se situent sur un même cercle en ne connaissant que la longueur de ses côtés.

Quadrangle et quadrilatère

Un quadrilatère dérive directement d'un quadrangle par le regroupement des sommets en deux paires. Pour chaque paire, les deux sommets sont dits opposés et le segment qui les joints (coté du quadrangle), n'est plus considéré comme un côté, mais comme une diagonale du quadrilatère.

Donc la première chose à savoir sur les quadrilatères quelconques, c'est que, contrairement aux triangles, la donnée de leurs sommets ne suffit pas à les définir (mais définit un quadrangle, sous certaines conditions).

En effet, considérons quatre points A, B, C et D (non alignés trois à trois pour éviter certains problèmes).
Ces quatre points sont les extrémités de six segments distincts : les six cotés du quadrangle : [AB], [AC], [AD], [BC], [BD] et [CD].
Ces segments peuvent être assemblés, quatre à quatre, pour former trois quadrilatères distincts (et trois seulement) :

• [AB] + [BC] + [CD] + [DA] noté ABCD,
• [AB] + [BD] + [DC] + [CA] noté ABDC,
• [AC] + [CB] + [BD] + [DA] noté ACBD.

Les quatre segments utilisés par le quadrilatère sont ses côtés ; les deux autres segments sont ses diagonales.

Notation

Ainsi ABCD est une notation commune pour définir un quadrangle ou un quadrilatère.
Cependant si l'ordre des points est indifférent pour un quadrangle, il doit en revanche être respecté (à une rotation ou un retournement près) pour conserver un même quadrilatère.

Il existe 24 arrangements des quatre points A, B, C et D basés sur le même quadrangle. Il y a trois quadrilatères ABCD, ACBD, ABDC.

Le même quadrilatère ABCD peut donc s'écrire ABCD, BCDA, CDAB, DABC dans un sens ; DCBA, CBAD, BADC, ADCB dans l'autre sens.

Typologie des quadrilatères

Les quadrilatères quelconques offrent relativement peu d'intérêt, mais permettent de voir ce qui se cache derrière les définitions des quadrilatères particuliers bien connus ( trapèze, parallélogramme, rectangle, losange, carré, Cerf-volant, Pseudo-carré, ... )

Classements

Quand on cherche à classer les quadrilatères en leur imposant des propriétés particulières, on obtient par exemple :

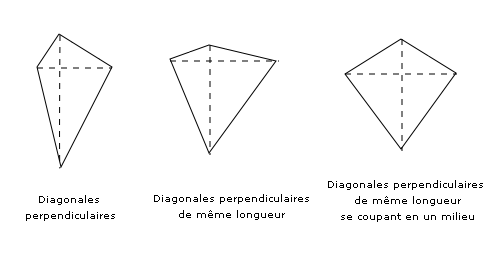
• les quadrilatères dont les diagonales sont perpendiculaires

les quadrilatères convexes dont les diagonales sont perpendiculaires:

L'aire de tous ces quadrilatères convexes est 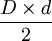(où D et d sont les mesures des diagonales).

Cette catégorie ne présente pas de régularité d'aspect.

Les quadrilatères dont les diagonales sont perpendiculaires et deux côtés consécutifs égaux : le cerf-volant, le losange , le cerf-volant concave dit "pointe de flèche".

Un quadrilatère dont les diagonales sont perpendiculaires et de même longueur : le pseudo-carré

• les quadrilatères dont les côtés sont égaux deux à deux :

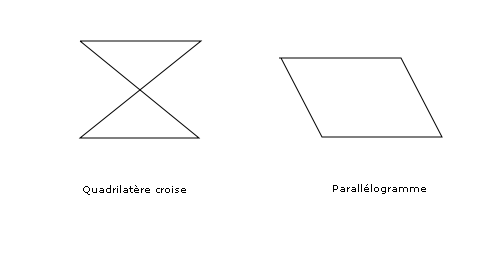
On n'obtient pas toujours un parallélogramme. Si les côtés égaux sont consécutifs deux à deux, on retombe sur le cerf-volant. Si le quadrilatère n'est pas convexe, on obtient un quadrilatère croisé : l'antiparallélogramme.

• les quadrilatères dont certains côtés sont parallèles :

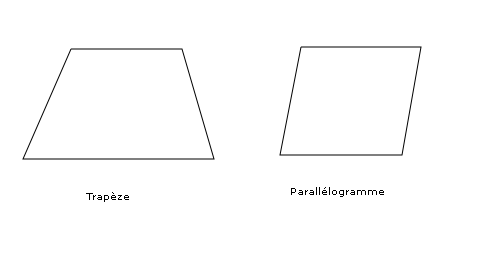
on retrouve là deux classes intéressantes de quadrilatères  : les trapèzes et les parallélogrammes.

• les parallélogrammes particuliers nous donnent les classes des rectangles (parallélogrammes à angles droits), des losanges (parallélogrammes à côtés adjacents égaux) et des carrés (à la fois rectangles et losanges).

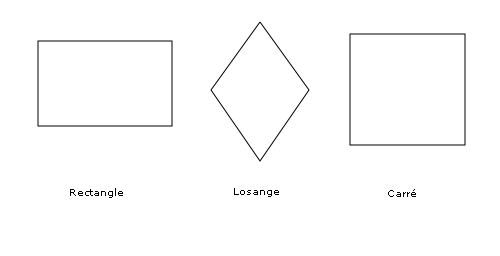
Ainsi, selon cette classification, le carré est le quadrilatère le plus riche en propriétés. Il est aussi l'unique solution du problème isopérimétrique pour les quadrilatères. C'est-à-dire que, parmi tous les quadrilatères de même périmètre, le carré est celui qui possède la plus grande surface.

• les quadrilatères inscriptibles dans un cercle : les sommets sont cocycliques.

Propriétés générales des quadrilatères convexes

1. La somme des angles d'un quadrilatère convexe vaut 360°. Mais cela n'est pas vrai pour un quadrilatère concave.
2. L'aire d'un quadrilatère convexe est égale au demi-produit des diagonales multiplié par le sinus de l'angle qu'elles forment (l'angle utilisé étant le plus petit des deux angles formés par les droites).
3. Un quadrilatère convexe ABCD (A B C et D tous distincts) est l'ensemble des points de l'intersection des demi-plans délimités par (AB), par (BC), par (CD) et par (DA) et contenant respectivement chacun les points C, D, A et B.

On déduis de 3. l'appartenance d'un point quelconque P au quadrilatère ABCD par le signe des inégalités des demi-plans.

P(x, y) appartient à ABCD équivaut à:

Signe (YB-YA)/(XB-XA)*(YC-XB)+YB-YC = Signe (YB-YA)/(XB-XA)*(x-XB)+YB-y
et Signe (YC-YB)/(XC-XB)*(YD-XC)+YC-YD = Signe (YC-YB)/(XC-XB)*(x-XC)+YC-y
et Signe (YD-YC)/(XD-XC)*(YA-XD)+YD-YA = Signe (YD-YC)/(XD-XC)*(x-XD)+YD-y
et Signe (YA-YD)/(XA-XD)*(YB-XA)+YA-YB = Signe (YA-YD)/(XA-XD)*(x-XA)+YA-y

Avec A(XA, YA) B(XB, YB) C(XC, YC) D(XD, YD)

Liens connexes

• quadrilatère complet
• antiparallélogramme

Références

Polygones

Henagone (1) • Digone (2) • Triangle (3) • Quadrilatère (4) • Pentagone (5) • Hexagone (6) • Heptagone (7) • Octogone (8) • Ennéagone (9) • Décagone (10) • Hendécagone (11) • Dodécagone (12) • Tridécagone (13) • Tétradécagone (14) • Pentadécagone (15) • Hexadécagone (16) • Heptadécagone (17) • Octadécagone (18) • Ennéadécagone (19) • Icosagone (20) • Triacontagone (30) • Tétracontagone (40) • Pentacontagone (50) • Hexacontagone (60) • Heptacontagone (70) • Octacontagone (80) • Ennéacontagone (90) • Hectogone (100) • Dihectogone (200) • Trihectogone (300) • Tétrahectogone (400) • Pentahectogone (500) • Hexahectogone (600) • Heptahectogone (700) • Octahectogone (800) • Ennéahectogone (900) • Chiliogone (1000) • Myriagone (10000)

• Portail de la géométrie