Quadrilatere complet

Quadrilatere complet: Quadrilatère complet

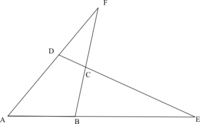
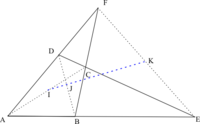
Un quadrilatère complet est une figure de géométrie plane constituée de quatre droites dont deux quelconques ne sont pas parallèles ni trois quelconques concourantes.

Une autre manière de définir un quadrilatère complet est de compléter un quadrilatère convexe ABCD par le point E intersection des droites (AB) et (CD) et le point F intersection des droites (AD) et (BC).

Cette figure est très liée à la géométrie projective et fut étudiée dès le II^e siècle par Menelaüs puis Pappus d'Alexandrie.

Sommaire

1 Propriétés

1.1 Une division harmonique sur les diagonales

1.2 La droite de Newton

1.3 Théorème de Miquel

2 Utilisation remarquable

3 Voir aussi

3.1 Article connexe

3.2 Liens externes

Propriétés

Une division harmonique sur les diagonales

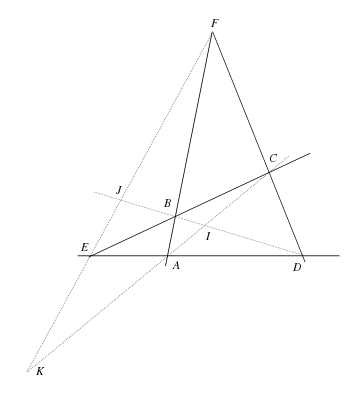
Chacune des trois diagonales [BD], [EF] et [AC] est divisée harmoniquement par les deux autres.

Chaque diagonale coupe les deux autres en créant des divisions harmoniques. De manière plus explicite la diagonale (BD) est coupée par les diagonales (AC) et (EF) en I et J tels que
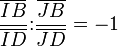
${\frac{\overline{IB}}{\overline{ID}}}\mathrel{:}{\frac{\overline{JB}}{\overline{JD}}}=-1$
De même si K est l'intersection des diagonales (AC) et (EF) :

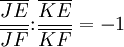
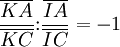
${\frac{\overline{JE}}{\overline{JF}}}\mathrel{:}{\frac{\overline{KE}}{\overline{KF}}}=-1$ ${\frac{\overline{KA}}{\overline{KC}}}\mathrel{:}{\frac{\overline{IA}}{\overline{IC}}}=-1$

C'est un avatar projectif de la propriété des diagonales du parallélogramme (cas où l'une des diagonales du quadrilatère complet est la droite à l'infini dans le plan projectif vu comme plan affine complété), à savoir qu'elles se coupent en leur milieu (cas limite de division harmonique, voir l'article).

On en donne une première démonstration géométrique, qui utilise les propriétés des faisceaux harmoniques : la propriété caractéristique qui est que toute sécante à un faisceau harmonique est découpée suivant une division harmonique, et l'existence et l'unicité d'une quatrième harmonique.

Démonstration Géométrique

Étant donné trois droites issues d'un point, il n'existe qu'une seule droite formant avec celles-là un faisceau harmonique.

Notons $[O | A 1, A 2, A 3, A 4]$ le faisceau des droites $(O A 1),(O A 2),(O A 3),(O A 4)$ (Les points $A 1, A 2, A 3, A 4$ n'étant pas forcément alignés).

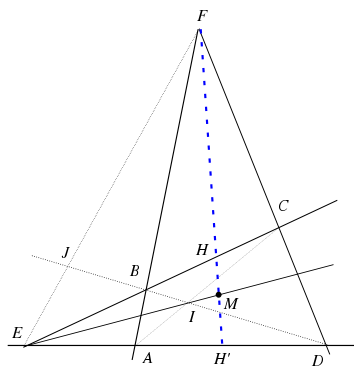
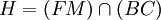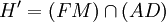Soit $I$ le point d'intersection des diagonales $(A C)$ et $(B D)$ . Soit $M$ l'unique point sur la droite $(E I)$ tel que le faisceau $[E | F, C, M, D]$ soit harmonique. Posons $H=(FM)\cap(BC)$ et $H'=(FM)\cap(AD)$ .

On a $[F | E, B, M, D] = [F | E, B, H, C]$ , de sorte que le faisceau $[I | E, B, H, C]$ est harmonique (rappelons que le fait d'être harmonique ne dépend que de la position des points d'intersection avec une sécante ; ici la sécante est la droite $(E C)$ ).

Pour une raison analogue, il en est de même de $[I | E, A, H', D]$ .

Mais comme $(I A) = (I C)$ et que $(I B) = (I D)$ , on a $[I | E, A, H', D] = [I | E, B, H', C]$ de sorte que les deux faisceaux $[I | E, B, H, C]$ et $[I | E, B, H', C]$ sont tous deux harmoniques et possèdent trois droites communes. En vertu de la propriété d'unicité, ces deux faisceaux sont identiques et par conséquent $(I H) = (I H')$ .

Ainsi 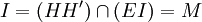$I=(HH')\cap(EI)=M$ par définition de $M$ .

Le faisceau $[F | J, B, I, D]$ est donc harmonique ce qui signifie que $[I, J]$ divise harmoniquement $[B, D]$

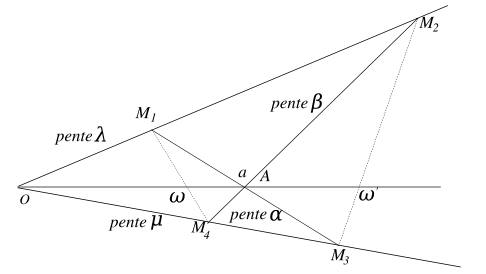
Démonstration Analytique

Soit $Y = λ X$ , $Y = μ X$ deux droites issues de $O$ . $A = (a,0)$ un point de l'axe des $x$ ; $Y = α(X - a)$ et $Y = β(X - a)$ deux droites issues de $A$ . On note $M i (x i, y i)$ les quatre points d'intersection.

On calcule facilement 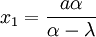$x_1=\frac{a\alpha}{ \alpha-\lambda}$ d'où l'on tire par permutation :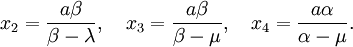 $\quad x_2=\frac{a\beta}{ \beta-\lambda},\quad x_3=\frac{a\beta}{ \beta-\mu},\quad x_4=\frac{a\alpha}{\alpha-\mu}.$

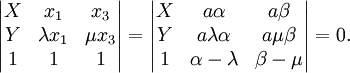
La droite $(M 1 M 3)$ a pour équation : $\quad\begin{vmatrix}X&x_1&x_3\\Y&\lambda x_1&\mu x_3\\1&1&1\end{vmatrix}= \begin{vmatrix}X&a\alpha&a\beta\\Y&a\lambda\alpha&a\mu\beta\\1&\alpha-\lambda&\beta-\mu\end{vmatrix}=0.$

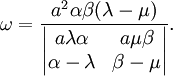
On en tire l'abscisse $ω$ du point d'intersection avec l'axe $O x$ : $\quad\omega=\frac{a^2\alpha\beta(\lambda-\mu)}{\begin{vmatrix}a\lambda\alpha&a\mu\beta\\\alpha-\lambda&\beta-\mu\end{vmatrix}}.$

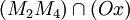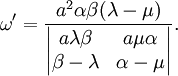
Par permutation on déduit celle $ω'$ de $(M_2M_4)\cap(Ox)$ : $\quad\omega'=\frac{a^2\alpha\beta(\lambda-\mu)}{\begin{vmatrix}a\lambda\beta&a\mu\alpha\\\beta-\lambda&\alpha-\mu\end{vmatrix}}.$

Il en résulte

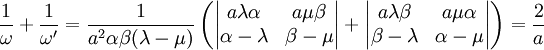
$\frac1\omega+\frac1{\omega'}=\frac1{a^2\alpha\beta(\lambda-\mu)}\left( \begin{vmatrix}a\lambda\alpha&a\mu\beta\\\alpha-\lambda&\beta-\mu\end{vmatrix}+ \begin{vmatrix}a\lambda\beta&a\mu\alpha\\\beta-\lambda&\alpha-\mu\end{vmatrix}\right)=\frac2a$

après développement des déterminants.

Remarque : on aurait pu prendre $a = 1$ mais la moyenne harmonique aurait été moins visible.

Cette propriété peut aussi se déduire du théorème de Ménélaüs et du théorème de Ceva, ou permettre de déduire l'un de ses théorèmes à partir de l'autre, voir ce dernier article.

La droite de Newton

Les milieux des trois diagonales sont alignés sur une droite appelée droite de Newton.

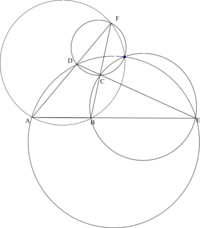
Théorème de Miquel

les cercles circonscrits aux triangles (EAD), (EBC), (FAB) et (FDC) sont concourants.

Article détaillé : Théorème de Miquel.

Utilisation remarquable

Le dual du quadrilatère complet est le quadrangle complet.

Le quadrangle complet inscrit dans une conique est très utile pour démontrer certaines propriétés des tangentes et des polaires dans une conique.

Voir aussi

Article connexe

Quadrilatère

Liens externes

quadrilatère complet sur Chronomath

quadrilatère complet sur le site de Debart

Articles de Géométrie projective ou voisins à consulter. [modifier]

Hexagramme de Pascal • Axiomes de plans projectifs • Théorème de Pappus • Théorème de Desargues • Dualité • Axiomes de plans projectifs/Suite des axiomes • Axiomes de plans projectifs/homogènes • Axiomes de plans projectifs/barycentriques • Plan affine • Théorème d'Hessenberg • Traité projectif des coniques • Traité projectif des coniques/Dans un plan pappusien • Conique • Octonions • Relation d'équivalence • Structure de corps • Construction d'un cercle point par point • Construction d'une parabole tangente par tangente • Plan de Fano • Portail:Géométrie • Géométrie analytique • Géométrie synthétique • Géométrie • Géométrie projective • Géométrie non euclidienne • Division harmonique • Rapport anharmonique • Application projective • Fonction homographique • Perspective • Perspective conique • Infini • Droite (mathématiques)

Portail de la géométrie

Ce document provient de « Quadrilat%C3%A8re complet ».

Catégories : Polygone | Géométrie projective

Contenu soumis à la licence CC-BY-SA. Source : Article Quadrilatere complet de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Quadrilatère complet — Un quadrilatère complet est une figure de géométrie plane constituée de quatre droites dont deux quelconques ne sont pas parallèles ni trois quelconques concourantes. Une autre manière de définir un quadrilatère complet est de compléter un… … Wikipédia en Français
Quadrilatère complet — ● Quadrilatère complet ensemble de quatre droites (côtés) se coupant (deux à deux) en six points (sommets) … Encyclopédie Universelle
Quadrilatere — Quadrilatère QUADRILATÈRES ┌─────────────┼─────────────┐ concave convexe croisé … Wikipédia en Français
Quadrilatère (mathématiques élémentaires) — Quadrilatère QUADRILATÈRES ┌─────────────┼─────────────┐ concave convexe croisé … Wikipédia en Français
Quadrilatère convexe — Quadrilatère QUADRILATÈRES ┌─────────────┼─────────────┐ concave convexe croisé … Wikipédia en Français
quadrilatère — [ k(w)adrilatɛr ] n. m. • 1694; adj. 1554; bas lat. quadrilaterus ♦ Polygone à quatre côtés. Quadrilatères convexes. ⇒ carré, losange, parallélogramme, rectangle, trapèze. ♢ Terrain d une forme analogue. « Un grand quadrilatère entouré de murs »… … Encyclopédie Universelle
Quadrilatère — Pour les articles homonymes, voir Quatre coins. Quadrilatères ┌─────────────┼─────────────┐ concave convexe croisé … Wikipédia en Français
Quardrilatéral — Quadrilatère QUADRILATÈRES ┌─────────────┼─────────────┐ concave convexe croisé … Wikipédia en Français
Division Harmonique — (A, B, C, D) est une division harmonique : En géométrie affine quatre points alignés sont en division harmonique quand ils vérifient l égalité des rappo … Wikipédia en Français
Division harmonique — (A, B, C, D) est une division harmonique : En géométrie affine quatre points alignés sont en division harmonique quand ils vérifient l égalité des rapports de mesure algébrique indiquée ci contre. El … Wikipédia en Français

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts