Processus continu

Pour les articles homonymes, voir Processus.

La notion de processus continu correspond à un type de processus stochastique utilisé dans la description des signaux physiques, fonctions généralement régulières du temps. Le présent article aborde en termes élémentaires cette notion assez abstraite en partant d'un phénomène particulier, les vagues en mer. On trouvera quelques précisions supplémentaires dans Processus stationnaire.

Probabilités dans un phénomène déterministe

Exemple d'un signal ayant une statistique gaussienne

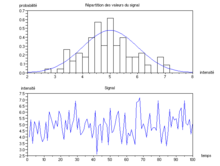
Un enregistrement de la surface de la mer en un point donné fournit les hauteurs mesurées à des intervalles de temps réguliers. On peut alors construire un histogramme qui regroupe en classes les différents niveaux et constater qu'il ressemble à celui d'une loi de Gauss ; un test statistique montrera que l'hypothèse n'est pas déraisonnable (même si, dans le cas particulier des vagues, l'histogramme présente une faible dissymétrie explicable physiquement). En poussant l'analyse, on pourra constater de même que l'histogramme des valeurs de crêtes est raisonnablement proche d'une loi de probabilité nommée loi de Rayleigh.

Ces résultats peuvent surprendre : si on met à part des circonstances particulières (effet du vent, déferlements, etc.), la mécanique des vagues est bien modélisée par les lois déterministes de la mécanique des fluides. Comment s'introduisent alors les lois de probabilité ? C'est ici qu'intervient la notion de processus stochastique.

Terminologie

Un processus stochastique est souvent appelé processus aléatoire (voir Calcul stochastique) ou, plus rarement, fonction aléatoire (voir Probabilité). Cette dernière expression aide à comprendre intuitivement de quoi il s'agit.

De même qu'une variable aléatoire est en fait un ensemble de nombres d'où l'on peut extraire un nombre particulier, une fonction aléatoire est un ensemble de fonctions ordinaires (tout au moins dans le cadre restreint considéré ici) d'où l'on peut extraire une fonction particulière.

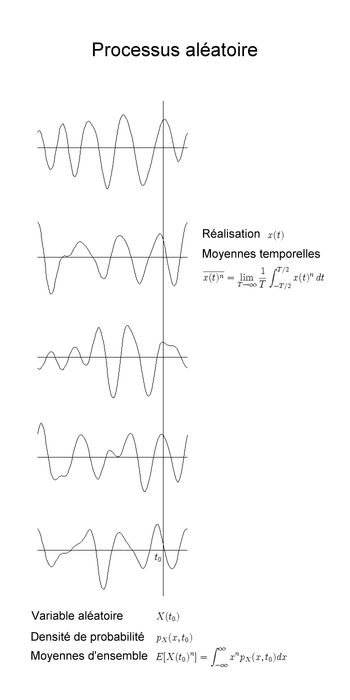
Cette fonction particulière s'appelle réalisation du processus. Elle représente l'aspect temporel du phénomène que l'on peut caractériser par des moyennes temporelles, moyennes des valeurs de la fonction élevées aux différentes puissances.

Le processus possède aussi un aspect probabiliste si on considère l'ensemble des valeurs à un instant donné comme une variable aléatoire. Cette dernière est décrite par une densité de probabilité ou – ce qui revient au même sous certaines conditions de régularité – par la suite des moments statistiques que l'on nomme moyennes d'ensemble.

Les moyennes d'ensemble dépendent, en principe, de l'instant auquel elles se rattachent. Si en fait elles n'en dépendent pas, les propriétés statistiques restent constantes au cours du temps et l'on dit que le processus est stationnaire.

Si, de plus, les moyennes temporelles sont identiques aux moyennes d'ensemble on dit que le processus est ergodique. Dans ces conditions, le phénomène est entièrement décrit par une seule réalisation. C'est donc cette notion d'ergodicité qui permet de répondre à la question posée initialement : comment interpréter en termes probabilistes un phénomène temporel même s'il est régi par des lois déterministes ?

Exemples

D'une certaine manière, le processus le plus simple est le bruit blanc qui possède une densité spectrale identique pour toutes les fréquences. Bien qu'un bruit blanc parfait ne puisse exister, cette notion peut fournir une approximation raisonnable d'une excitation quelconque d'un système peu amorti.

Une analyse approfondie des enregistrements de vagues conduit à les considérer comme des sommes d'une infinité de sinusoïdes infiniment petites (voir Analyse spectrale). En associant à ces sinusoïdes des phases aléatoires supposées indépendantes on construit un processus aléatoire stationnaire, ergodique et gaussien. Comme pour les variables aléatoires, cette dernière hypothèse simplifie considérablement le problème. À cause de sa simplicité relative, ce cas est particulièrement important dans les domaines les plus divers. Cependant il faut parfois s'attaquer à des problèmes plus difficiles.

Ainsi en considérant, au cours de différents atterrissages d'un avion, les efforts dans une pièce de liaison du train on obtient des signaux qui ont une vague allure de sinusoïde amortie et que l'on peut regrouper dans un processus. Il est clair que les moyennes d'ensemble ne sont pas constantes, le processus n'est pas stationnaire, ce qui exclut toute interrogation sur une ergodicité éventuelle.

D'autre part, des signaux de niveaux constants situés entre deux extrêmes peuvent être de toute évidence interprétés comme des réalisations d'un processus stationnaire mais ce sont alors les moyennes temporelles qui ne sont pas définies.

Ces quelques exemples indiquent que les processus stationnaires ergodiques sont particulièrement intéressants, surtout s'ils sont gaussiens. Dans tel problème concret, on peut être amené à considérer des processus non stationnaires, donc non ergodiques, au prix d'une plus grande quantité de données d'observation et d'un appareil mathématique plus compliqué. En revanche, les processus stationnaires non ergodiques semblent se réduire à des curiosités mathématiques.

Illustration

Livres

• (en) (en) Y. K. Lin, Probabilistic Theory of Structural Dynamics, New York, Robert E. Krieger Publishing Company, juillet 1976, 368 p. (ISBN 0882753770) 

• Portail des probabilités et des statistiques