Processus aléatoire

Processus aléatoire: Processus stochastique

Pour les articles homonymes, voir Processus.

Le calcul des probabilités classique concerne des épreuves où chaque résultat possible (ou réalisation) est un nombre, ce qui conduit à la notion de variable aléatoire. Un processus stochastique ou processus aléatoire (voir Calcul stochastique) ou fonction aléatoire (voir Probabilité) représente une évolution, généralement dans le temps, d'une variable aléatoire.

Sommaire

1 Mathématiquement

2 Espace des trajectoires

3 Pratiquement

3.1 Notion de processus

3.2 Types de processus

3.3 Exemples

4 Voir aussi

4.1 Articles connexes

4.2 Liens externes

4.3 Livres

Mathématiquement

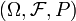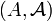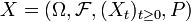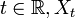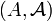Soit $(\Omega , \mathcal F , P )$ un espace de probabilité. On appelle processus aléatoire à valeur dans $(A, \mathcal A)$ un élément $X = (\Omega,\mathcal F,(X_t)_{t\ge 0},P)$ , où pour tout $t\in \mathbb{R}, X_t\,$ est une variable aléatoire à valeur dans $(A,\mathcal A)$ .

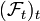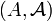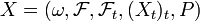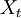Si $({\mathcal F}_t)_t\,$ est une filtration, on appelle processus aléatoire adapté, à valeur dans $(A,\mathcal A)$ , un élément $X=(\omega,\mathcal F,\mathcal{F}_t,(X_t)_t,P)$ où $X_t\,$ est une variable aléatoire 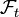$\mathcal{F}_t$ -mesurable à valeur dans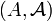 $(A,\mathcal A)$

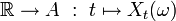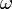La fonction $\mathbb R \rightarrow A\ : \ t \mapsto X_t(\omega)$ est appelée la trajectoire associée à la réalisation $\omega \,$ .

Espace des trajectoires

On appelle espace des trajectoires l'ensemble 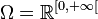$\Omega=\mathbb{R}^{[0,+\infty[}$ . Pour 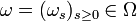$\omega=(\omega_s)_{s\ge 0}\in\Omega$ , on peut alors poser, pour $t > 0$ , $X t (ω) = ω t$ .

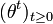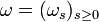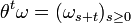On est souvent amené, notamment dans l'étude des processus markoviens, à introduire la famille des opérateurs de translation $(\theta^t)_{t\ge 0}$ . Pour $\omega=(\omega_s)_{s\ge 0}$ , $\theta^t\omega=(\omega_{s+t})_{s\ge 0}$ .

Les opérateurs 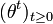$(\theta^t)_{t\ge 0}$ forment un semi-groupe puisque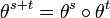 $\theta^{s+t}=\theta^{s}\circ\theta^t$

On a $X s (θ t ω) = X s + t (ω) = ω s + t$ , en particulier $X 0 (θ t ω) = X t (ω) = ω t$ .

Pratiquement

Notion de processus

De nombreux domaines utilisent des observations en fonction du temps (ou, plus exceptionnellement, d'une variable d'espace). Dans les cas les plus simples, ces observations se traduisent par une courbe bien définie. Malheureusement, des sciences de la Terre aux sciences humaines, les observations se présentent souvent de manière plus ou moins erratique. Il est donc tentant d'introduire des probabilités.

Un processus aléatoire généralise la notion de variable aléatoire utilisée en statistiques élémentaires. On le définit comme une famille de variables aléatoires 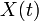$X(t)\,$ qui associe une telle variable à chaque valeur 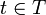$t \in T\,$ . L'ensemble des observations disponibles 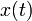$x(t)\,$ constitue une réalisation du processus.

Un premier problème concerne le fait que la durée sur laquelle est construit le processus est généralement infinie alors qu'une réalisation porte sur une durée finie. Il est donc impossible de représenter parfaitement la réalité. Il y a une seconde difficulté beaucoup plus sérieuse : à la différence du problème des variables aléatoires, la seule information disponible sur un processus se réduit généralement à une seule réalisation.

Types de processus

On distingue généralement les processus en temps discret et en temps continu, à valeurs discrètes et à valeurs continues.

Si l'ensemble 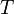$T\,$ est dénombrable on parle de processus discret ou de série temporelle, si l'ensemble est indénombrable on parle de processus continu. La différence n'a rien de fondamental : en particulier la stationnarité, constance en fonction du temps des propriétés statistiques, se définit de la même façon. Il ne s'agit même pas d'une différence pratique car les calculs sur un processus continu s'effectuent à partir de l'échantillonnage d'une réalisation du processus. La différence porte plutôt sur l'attitude adoptée face à l'utilisation d'une seule réalisation.

Il existe une différence un peu plus nette entre les processus à valeurs continues et les processus de comptage à valeurs discrètes. Les seconds remplacent par des sommes algébriques les intégrales utilisées par les premiers.

Exemples

En matière de processus à valeurs continues, les processus de Gauss sont particulièrement utilisés pour les mêmes raisons que les variables de Gauss en statistiques élémentaires. Une application intuitive du théorème de la limite centrale conduit à penser que bon nombre de phénomènes, dus à des causes nombreuses, sont approximativement gaussiens. D'autre part, un tel processus présente l'avantage d'être entièrement défini par ses caractéristiques au second ordre, espérance et autocovariance.

La description d'un phénomène par des valeurs discrètes conduit à des processus de comptage dont le plus simple est le processus de Poisson utilisé dans la théorie des files d'attente

La notion de propriété markovienne définit une classe de processus discrets ou continus, à valeurs discrètes ou continues, qui repose sur l'hypothèse selon laquelle l'avenir ne dépend que de l'instant présent.

Voir aussi

Articles connexes

Processus continu

Rapport signal sur bruit

Mouvement brownien

Approche écosystémique

Liens externes

Page probabilités et statistiques d'Avner Bar-Hen

Livres

Comets, F. & Meyre, T : "Calcul stochastique et modèles de diffusions", Dunod (2006). ISBN : 9782100501359

Lin, Y. K. : "Probabilistic Theory of Structural Dynamics", Robert E. Krieger Publishing Company, New York (1967)

Articles de mathématiques en rapport avec les probabilités ou les statistiques

Statistiques descriptives • Analyse des données • Visualisation des données • Estimateurs • Tests statistiques • Séries temporelles et économétrie • Statistique Mathématique • Théorie des probabilités • Variables aléatoires • Inégalités • Théorèmes limites • Processus stochastiques • La mécanique statistique • Les statistiques et l'économie • Les statistiques et la sociologie • Les statistiques et les sciences • Les probabilités et les jeux • Les équations aux dérivées partielles et les probabilités

Portail des probabilités et des statistiques

Ce document provient de « Processus stochastique ».

Catégorie : Processus stochastique

Contenu soumis à la licence CC-BY-SA. Source : Article Processus aléatoire de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

processus aléatoire — atsitiktinis vyksmas statusas T sritis Standartizacija ir metrologija apibrėžtis Tikimybinių veiksnių lemiamas vyksmas. atitikmenys: angl. random process; stochastic process vok. stochastischer Prozess, m; zufälliger Prozess, m rus. случайный… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
processus aléatoire — atsitiktinis vyksmas statusas T sritis fizika atitikmenys: angl. random process vok. zufälliger Prozeß, m rus. случайный процесс, m pranc. processus aléatoire, m; processus stochastique, m … Fizikos terminų žodynas
processus aléatoire — stochastinis vyksmas statusas T sritis fizika atitikmenys: angl. stochastic process vok. stochastischer Vorgang, m rus. стохастический процесс, m pranc. processus aléatoire, m; processus stochastique, m … Fizikos terminų žodynas
processus aléatoire — atsitiktinis procesas statusas T sritis automatika atitikmenys: angl. random process vok. stochastischer Prozeß, m; Zufallsprozeß, m rus. случайный процесс, m pranc. processus aléatoire, m … Automatikos terminų žodynas
Processus aléatoire stationnaire — ● Processus aléatoire stationnaire processus dont les propriétés statistiques ne dépendent pas de l origine des temps … Encyclopédie Universelle
Processus stochastiques — Processus stochastique Pour les articles homonymes, voir Processus. Le calcul des probabilités classique concerne des épreuves où chaque résultat possible (ou réalisation) est un nombre, ce qui conduit à la notion de variable aléatoire. Un… … Wikipédia en Français
Processus de gauss — Cette notion se rencontre dans des domaines variés allant des vibrations mécaniques aux vagues de la mer. De même que le théorème de la limite centrale permet de considérer une somme de variables aléatoires indépendantes comme une variable de… … Wikipédia en Français
aléatoire — [ aleatwar ] adj. • 1596; lat. aleatorius, de alea 1 ♦ Dr. Contrat aléatoire : convention réciproque dont les effets, quant aux avantages et aux pertes, dépendent d un événement incertain, par ex. jeu, pari, contrat de vente viagère. 2 ♦ (1845)… … Encyclopédie Universelle
Processus stochastique — Pour les articles homonymes, voir Processus. Le calcul classique des probabilités concerne des épreuves où chaque résultat possible (ou réalisation) est mesuré par un nombre, ce qui conduit à la notion de variable aléatoire. Un processus… … Wikipédia en Français
Processus continu — Pour les articles homonymes, voir Processus. La notion de processus continu correspond à un type de processus stochastique utilisé dans la description des signaux physiques, fonctions généralement régulières du temps. Le présent article aborde en … Wikipédia en Français

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts