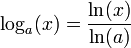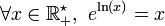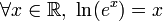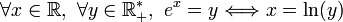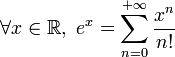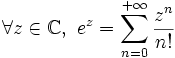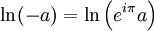- Logarithme népérien
-
Logarithme naturel
Le logarithme naturel ou logarithme népérien, est, en mathématiques, le logarithme de base e. C'est la réciproque de la fonction exponentielle de base e. C'est la primitive de la fonction inverse définie sur
![]0 ; + \infty[](/pictures/frwiki/97/abe7a92275e0c5644d5bd5c819fa694e.png) et qui s'annule en 1.
et qui s'annule en 1.Le logarithme naturel de x est la puissance à laquelle il faut élever e pour trouver x.
Cette fonction a été longtemps notée Log pour la différencier de la fonction log (logarithme de base quelconque, ou plus particulièrement logarithme décimal). On préfère de nos jours la notation ln.
Fragments d'histoire
Article d'une série sur la constante mathématique e 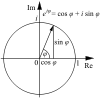
Logarithme naturel Applications Intérêts composés · Identité d'Euler et Formule d'Euler · Demi-vie et Croissance exponentielle/Décroissance exponentielle Définitions Démonstration de l'irrationalité de e · Représentations de e · Théorème de Lindemann-Weierstrass Personnes John Napier · Jacques Bernoulli · Leonhard Euler Conjecture de Schanuel Ce logarithme est appelé logarithme népérien en hommage au mathématicien écossais John Napier qui est à l'origine des premières tables logarithmiques. Celles-ci ne furent cependant pas des tables de logarithmes népériens[1]. On date en général la naissance des logarithmes népériens de 1647, date à laquelle Grégoire de Saint-Vincent travaille sur la quadrature de l'hyperbole et démontre que la fonction obtenue vérifie la propriété des fonctions logarithmes (transformation d'un produit en somme) mais lui-même ne voit pas le lien avec les logarithme inventé par Napier et c'est son disciple Alphonse Antoine de Sarasa qui l'explicitera en 1649[2]. La fonction ln s'est d'ailleurs appelée un certain temps fonction logarithme hyperbolique compte tenu de sa découverte comme aire sous l'hyperbole[3]. Le terme de logarithme naturel apparaît pour la première fois dans une note de Nicolaus Mercator en 1668, quand celui-ci met en place sa série de Mercator[4]. Sa série exploitée par Newton (méthode des fluxions et des suites infinies 1671), permet de calculer assez simplement les valeurs du logarithme de Grégoire de Saint-Vincent[5]. Le calcul des autres logarithmes apparaît alors bien compliqué. Le logarithme de Grégoire de Saint-Vincent devient alors le logarithme le plus "simple" et le plus naturel.
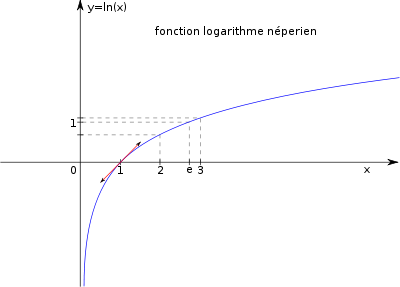
La fonction logarithme naturel comme primitive de la fonction inverse
Formellement, le logarithme naturel peut être défini comme l'aire du domaine délimité par la courbe représentative de la fonction
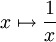 , l'axe des abscisses et les droites d'abscisses 1 et x.
, l'axe des abscisses et les droites d'abscisses 1 et x.La fonction
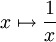 est une fonction continue sur
est une fonction continue sur ![]0 ; + \infty[](/pictures/frwiki/97/abe7a92275e0c5644d5bd5c819fa694e.png) . Elle admet donc des primitives dont l'une s'annule en 1. Cette primitive est appelée logarithme naturel et est donc définie par :
. Elle admet donc des primitives dont l'une s'annule en 1. Cette primitive est appelée logarithme naturel et est donc définie par :Propriétés immédiates
Il est alors immédiat de dire que le logarithme naturel est défini sur
![]0 ; + \infty[](/pictures/frwiki/97/abe7a92275e0c5644d5bd5c819fa694e.png) , dérivable sur
, dérivable sur ![]0 ; + \infty[](/pictures/frwiki/97/abe7a92275e0c5644d5bd5c819fa694e.png) et que pour
et que pour 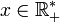
Puisque sa dérivée est strictement positive, on en déduit que le logarithme naturel est strictement croissant.
La fonction f définie par f(x) = ln(ax) pour a et x des réels strictement positifs a même dérivée que le logarithme naturel, donc diffère du logarithme naturel d'une constante
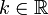 :
:- f(x) = ln(x) + k
Or f(1) = ln(a) donc k = ln(a) et ln(ax) = ln(a) + ln(x) pour tous réels a et x strictement positifs. Le logarithme naturel est donc bien un cas particulier de fonction logarithme.
C'est l'application réciproque de la fonction exponentielle, quand celle-ci est définie comme l'unique fonction valant 1 en 0 et égale à sa dérivée. En effet, il suffit de dériver les fonctions
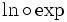 et
et 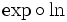 , de prouver que ces dérivés valent 1. Cela permet de dire que ces deux fonctions sont de la forme x + k. L'étude de l'image de 0 ou de l'image de 1 permet de prouver que ces deux fonctions sont des fonctions identités sur
, de prouver que ces dérivés valent 1. Cela permet de dire que ces deux fonctions sont de la forme x + k. L'étude de l'image de 0 ou de l'image de 1 permet de prouver que ces deux fonctions sont des fonctions identités sur  pour la première, sur
pour la première, sur ![]0 ; + \infty[](/pictures/frwiki/97/abe7a92275e0c5644d5bd5c819fa694e.png) pour la seconde.
pour la seconde.Dérivée logarithmique
Article détaillé : dérivation logarithmique.Les propriétés de dérivabilité des fonctions composées permettent de dire que, pour toute fonction u réelle, dérivable et strictement positive, la fonction
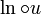 est dérivable de dérivée :
est dérivable de dérivée :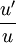 Cette dérivée s'appelle la dérivée logarithmique de la fonction u. Elle représente une variation instantanée relative. C'est donc une mesure utile tant en économie qu'en calcul d'erreur.
Cette dérivée s'appelle la dérivée logarithmique de la fonction u. Elle représente une variation instantanée relative. C'est donc une mesure utile tant en économie qu'en calcul d'erreur.On généralise la propriété à toute fonction réelle dérivable u qui ne s'annule pas
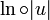 est dérivable de dérivée
est dérivable de dérivéeCette propriété augmente de manière significative l'ensemble des fonctions rationnelles dont on peut trouver une primitive.
Étude des limites
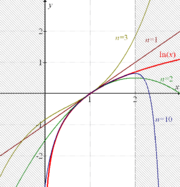
La fonction logarithme est une fonction tendant vers l'infini en 0 et en
 mais ceci très lentement. Plus précisément, les limites suivantes permettent de déterminer les croissances comparées du logarithme naturel et d'une fonction puissance quelconque
mais ceci très lentement. Plus précisément, les limites suivantes permettent de déterminer les croissances comparées du logarithme naturel et d'une fonction puissance quelconque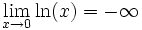
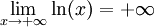
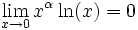 pour tout réel α strictement positif
pour tout réel α strictement positif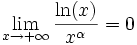 pour tout réel α strictement positif
pour tout réel α strictement positif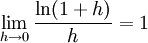 pour h > − 1. Ceci est une conséquence de l'"approximation affine" de ln(1 + h) pour h proche de 0.
pour h > − 1. Ceci est une conséquence de l'"approximation affine" de ln(1 + h) pour h proche de 0.
Développement en série
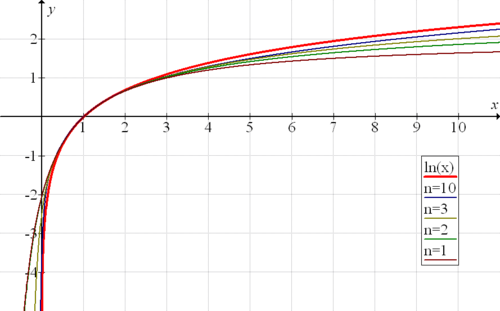
Article détaillé : série entière.C'est Nicolaus Mercator qui a été le premier à proposer le développement en série entière de ln(1 + x); le rayon de convergence de ce développement est 1. On a donc
C'est la série de Taylor pour le logarithme naturel, mais pour calculer la valeur numérique du logarithme naturel d'un nombre, on peut réécrire l'expansion de la série de Taylor avec:
Pour obtenir un meilleur taux de convergence, l'identité suivante peut être utilisée.
A condition que
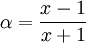 et x > 0. Ce qui nous amène à:
et x > 0. Ce qui nous amène à:La fonction logarithme naturel comme fonction logarithme
Article détaillé : identités logarithmiques.Comme toute fonction logarithme, elle possède les propriétés algébriques suivantes
Le fait que toutes les fonctions logarithmes soient proportionnelles entre elles permet d'obtenir le logarithme de base
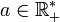 en fonction du logarithme népérien:
en fonction du logarithme népérien:La fonction logarithme naturel comme réciproque de la fonction exponentielle
Des égalités
et
on déduit l'équivalence suivante:
qui permet de résoudre des équations dans lesquelles l'inconnue apparaît en exposant.
Sa relation avec la fonction exponentielle permet d'exprimer toutes les autres fonctions exponentielles de base
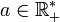 par
par- ax = exln(a).
Plus généralement , elle permet de définir xy pour tout réel x strictement positif et tout réel y comme
- xy = eyln(x)
Cette définition coïncide évidemment avec celle de xr pour r rationnel.
On peut aussi trouver la fonction inverse comme étant la dérivée du logarithme naturel uniquement en considérant cette dernière comme réciproque de la fonction exponentielle.
DémonstrationLa fonction exp est dérivable sur tout
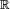 , de dérivée non nulle. Sa courbe représentative possède donc en tout point une tangente non parallèle à l'axe des abscisses. La courbe représentative de sa réciproque est symétrique de celle-ci par rapport à la droite d'équation y = x. Elle possède donc en tout point une tangente non parallèle à l'axe des ordonnées. Cela assure que la fonction ln est dérivable en tout point de son ensemble de définition.
, de dérivée non nulle. Sa courbe représentative possède donc en tout point une tangente non parallèle à l'axe des abscisses. La courbe représentative de sa réciproque est symétrique de celle-ci par rapport à la droite d'équation y = x. Elle possède donc en tout point une tangente non parallèle à l'axe des ordonnées. Cela assure que la fonction ln est dérivable en tout point de son ensemble de définition.On considère alors la fonction
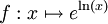 définie pour tout x > 0.
définie pour tout x > 0.L'égalité :
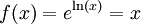 permet de calculer f' de deux manières.
permet de calculer f' de deux manières.- D'une part, selon la propriété de la dérivée de la composée :
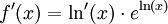 (car
(car 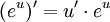 )
)- donc
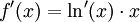
- D'autre part,
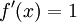
Donc
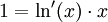
D'où
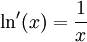
La fonction logarithme naturel comme fonction de la variable complexe
Article détaillé : logarithme complexe.La question de savoir s'il est possible de prolonger le logarithme naturel (c'est-à-dire de le définir sur un ensemble plus grand que
![]0 ; + \infty[](/pictures/frwiki/97/abe7a92275e0c5644d5bd5c819fa694e.png) ) s'est posée dès la seconde moitié du XVIIe siècle avec les développements en série des fonctions. Le passage de
) s'est posée dès la seconde moitié du XVIIe siècle avec les développements en série des fonctions. Le passage deà
s'est fait de manière naturelle et l'on se serait attendu à ce qu'un passage analogue se fasse pour le logarithme naturel. Mais il n'existe aucune fonction univoque continue sur
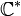 , possédant la propriété algébrique des fonctions logarithmes et coïncidant sur
, possédant la propriété algébrique des fonctions logarithmes et coïncidant sur ![]0 , + \infty[](/pictures/frwiki/101/eb8a0ceeec2805d7e3ba7c0591eafa52.png) avec la fonction logarithme népérien réelle.
avec la fonction logarithme népérien réelle.L'existence de plusieurs valeurs possibles pour ln( − 1), par exemple, a donné lieu à des échanges de lettres passionnés entre Leibniz et Bernoulli. Le voile sera levé par Euler[6].
On peut cependant définir le logarithme d'un nombre négatif de la manière suivante :
- ln( − a) = ln(a) + iπ pour a réel strictement positif
en référence au fait que
et par transfert de propriété :
- ln( − a) = ln(a) + iπ
Mais la fonction ainsi définie n'a pas les propriétés algébriques de la fonction logarithme népérien réelle. On peut la rencontrer lorsqu'on travaille avec une calculatrice traitant les nombres complexes : si l'on étudie la fonction
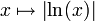 , la calculatrice peut être amenée à définir cette fonction sur
, la calculatrice peut être amenée à définir cette fonction sur 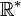 en interprétant la valeur absolue comme un module :
en interprétant la valeur absolue comme un module :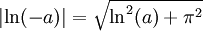 pour a réel strictement positif
pour a réel strictement positif
Voir aussi
Notes et références
- ↑ Amy Dahan-Dalmedico, Jeanne Peiffer, Une Histoire des mathématiques - Routes et dédales, Seuil, coll. « Points Sciences », 1986 (ISBN 2020092380)[détail des éditions], p 214
- ↑ Jean-Pierre Le Goff, De la méthode dite d'exhaustion - Grégoire de Saint Vincent, in La démonstration mathématique dans l'histoire, IREM de Besançon
- ↑ Simone Trompler, L'histoire des logarithmes, ULB p 11
- ↑ Logarithme et quadrature de l'hyperbole Sur le site Euler de l'académie de Versailles, p3
- ↑ Simone Trompler, L'histoire des logarithmes, ULB p 12
- ↑ Analyse de cette controverse, écrite en français par Euler lui-même
Articles connexes
- Logarithme
- Fonction exponentielle
- Logarithme décimal
- Logarithme discret
- Logarithme complexe
- Logarithme intégral
- Fonction W de Lambert
- e (nombre)
Lien externe
- Méthode de Newton pour le calcul des logarithmes naturels , La méthode des fluxions et des suites infinies Gallica , p 102 -105
- En quoi les logarithmes et exponentielles naturels sont-ils naturels ? Conférence de Jean Dhombres
- Portail des mathématiques
Catégories : Analyse réelle | Fonction remarquable | Logarithme
Wikimedia Foundation. 2010.

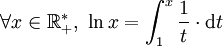
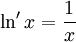
![\forall x \in ]-1,1[,\ \ln(1 + x) = \sum_{n = 0}^{+\infty}(-1)^n\frac{x^{n+1}}{n+1} = x - \frac{x^2}{2}+ \frac{x^3}{3}- \cdots](/pictures/frwiki/101/ee6d710809d2c553f9e7f0acd22035a6.png)
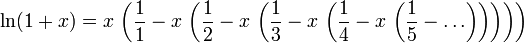
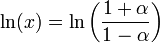
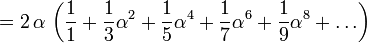
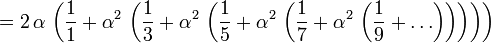
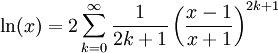
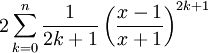 .
.![\forall (a;b)\in ]0 : + \infty[^2,\ \ln(ab) = \ln(a) + \ln(b)](/pictures/frwiki/52/4bd9fd373d0a9a2c704c8cb6b3b99d14.png)
![\forall (a;b)\in ]0 : + \infty[^2,\ \ln\left(\frac ab\right) = \ln(a) - \ln(b)](/pictures/frwiki/100/d4f0b7e5565009c81fcf406b1e7d0e81.png)
![\forall a \in ]0 ; + \infty[,\ \forall n \in \mathbb Z,\ \ln(a^n) = n \ln(a) \quad](/pictures/frwiki/100/dff2e77ec913cbe32ad24fefbd0246b3.png)
![\forall a \in ]0 ; + \infty[,\ \forall r \in \mathbb Q,\ \ln(a^r) = r \ln(a)](/pictures/frwiki/57/9be07f24946cc19749b4efae9cbbb88f.png)