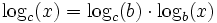Logarithme Discret

Logarithme discret

En algèbre générale et dans ses applications d'arithmétique modulaire, le logarithme discret est défini en théorie des groupes par analogie avec le logarithme ordinaire.

On considère un groupe cyclique G d'ordre n (dont la loi sera notée multiplicativement) et un générateur b de G. Alors chaque élément x de G peut être écrit sous la forme x = b^k pour un certain entier k ; de plus, deux quelconques de ces entiers sont nécessairement congrus modulo n. Il est ainsi possible de définir une fonction $log b$ de $G$ dans $Z n$ (où $Z n$ désigne l'anneau des entiers modulo n) en associant à tout élément x de $Z n$ la classe de congruence de k modulo n. Cette fonction est un isomorphisme de groupe, appelé logarithme discret de base b.

La formule familière de changement de bases pour les logarithmes ordinaires reste valide : si c est un autre générateur de G, alors :

$\log_c (x) = \log_c(b) \cdot \log_b(x)$

Pour certains groupes, le calcul des logarithmes discrets s'avère difficile, tandis que le problème inverse de l'exponentiation discrète ne l'est pas ; cette asymétrie est exploitée dans certaines applications en cryptologie.

Les choix populaires de G en cryptologie sont les groupes cycliques (Z_p)^× (constitués des nombres {1,...,p − 1} muni de la multiplication modulo le nombre premier p) ; voir le logarithme discret du cryptosystème d'ElGamal, l'échange de clés Diffie-Hellman et l'algorithme de signature numérique DSA.

Il est peut-être plus simple de comprendre les logarithmes discrets dans ce groupe avec un exemple :

Pour trouver la k^ieme puissance de l’un des nombres de ce groupe, ce qui se nomme exponentiation discrète, il faut élever ce nombre à la puissance k et calculer le reste de la division par p. Par exemple : 3⁵ = 243. Le reste de la division entière de 243 par 7 étant 5, 3⁵ dans le groupe (Z₇)^× est 5. Le logarithme discret est le problème inverse : étant donné 3^k ≡ 5 (mod 7), quel est le plus petit k pour lequel cette proposition est vraie ?

L'algorithme de Pohlig-Hellman peut être utilisé pour calculer les logarithmes discrets dans ces groupes si p-1 est un produit de petits nombres premiers, ce qui oblige à l'éviter dans ce genre d'applications. Le calcul d'index est une autre méthode pour calculer les logarithmes discrets dans ces groupes, comme l'attaque anniversaire.

Des applications plus récentes de la cryptologie utilisent les logarithmes discrets dans les sous-groupes cycliques de courbes elliptiques sur les corps finis. Voir cryptologie sur les courbes elliptiques.

Portail des mathématiques
Portail de la cryptologie

Ce document provient de « Logarithme discret ».

Catégories : Théorie algorithmique des nombres | Cryptologie | Logarithme | Théorie des groupes

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Logarithme Discret de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Logarithme discret — En algèbre générale et dans ses applications d arithmétique modulaire, le logarithme discret est défini en théorie des groupes par analogie avec le logarithme ordinaire. On considère un groupe cyclique G d ordre n (dont la loi sera notée… … Wikipédia en Français
Logarithme Naturel — Le logarithme naturel ou logarithme népérien, est, en mathématiques, le logarithme de base e. C est la réciproque de la fonction exponentielle de base e. C est la primitive de la fonction inverse définie sur et qui s annule en 1. Le logarithme… … Wikipédia en Français
Logarithme Népérien — Logarithme naturel Le logarithme naturel ou logarithme népérien, est, en mathématiques, le logarithme de base e. C est la réciproque de la fonction exponentielle de base e. C est la primitive de la fonction inverse définie sur et qui s annule en… … Wikipédia en Français
Logarithme naturel — Le logarithme naturel ou logarithme népérien est, en mathématiques, la fonction logarithme de base e. C est donc la réciproque de la fonction exponentielle de base e. C est aussi la primitive définie sur ] 0 , + ∞ [ et qui s annule en 1 de la… … Wikipédia en Français
Logarithme népérien — Logarithme naturel Le logarithme naturel ou logarithme népérien, est, en mathématiques, le logarithme de base e. C est la réciproque de la fonction exponentielle de base e. C est la primitive de la fonction inverse définie sur et qui s annule en… … Wikipédia en Français
Logarithme — Fonctions logarithmes : en rouge la fonction logarithme de base e, en vert celle de base 10 et en violet celle de base 1,7. Le logarithme de base b d un nombre réel positif est la … Wikipédia en Français
Fonction logarithme (mathématiques élémentaires) — Logarithme naturel Le logarithme naturel ou logarithme népérien, est, en mathématiques, le logarithme de base e. C est la réciproque de la fonction exponentielle de base e. C est la primitive de la fonction inverse définie sur et qui s annule en… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Diffie-Hellman — Échange de clés Diffie Hellman En cryptographie, l échange de clés Diffie Hellman, du nom de ses auteurs Whitfield Diffie et Martin Hellman, est une méthode par laquelle deux personnes nommées conventionnellement Alice et Bob peuvent se mettre d… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Logarithme Discret