Quadrature (mathematiques)

En mathématiques, la quadrature d'une surface est la recherche d'un carré ayant même aire que la surface en question. Si dans le langage courant le terme de quadrature revêt le sens d'opération impossible, cela provient du fait que la quadrature la plus célèbre (la quadrature du cercle) se révèle impossible à réaliser à la règle et au compas. Mais, en mathématiques, le terme de quadrature va prendre très rapidement le sens de calcul d'aire. Jusqu'à la fin du XVII^e siècle, le calcul intégral est inconnu et ces calculs d'aires ne peuvent se faire qu'en utilisant des calculs approchés mettant en place des méthodes comme la méthode d'exhaustion d'Archimède, la méthode des indivisibles de Cavalieri....

La recherche de ces quadratures fait un bond prodigieux (1669 - 1704) grâce à Leibniz et Newton, qui, avec le calcul infinitésimal, font le lien entre quadrature et dérivée.

Depuis cette époque, la recherche des quadratures est associée à celle des primitives : l'aire de la surface délimitée par les droites d'équation x = a et x = b, l'axe (Ox) et la courbe d'équation y = f(x), où f est une fonction positive est 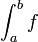(x)dx ; l'unité d'aire est fournie par l'aire du rectangle unité OINJ où I(1;0) et J(0;1)

Sommaire 1 Quadratures célèbres 1.1 Quadrature du cercle 1.2 Quadrature de la parabole 1.3 Quadratures des fonctions de kxm 1.4 Quadrature de la cycloïde 1.5 Quadrature de l'hyperbole y = 1/x 2 Voir aussi

Quadratures célèbres

Quadrature du cercle

• Voir article détaillé : quadrature du cercle

C'est un problème vieux de plus de 2000 ans, posé par l'école pythagoricienne : peut-on tracer à la règle et au compas un carré ayant même aire qu'un cercle donné ? La réponse à cette question ne viendra que plus de 19 siècles plus tard grâce à Pierre-Laurent Wantzel, Joseph Liouville et Ferdinand von Lindemann : la réponse est non. Le calcul de l'aire d'un disque de rayon r est pourtant réalisable : c'est πr². Cependant le carré qu'il faudrait construire aurait pour côté 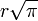, construction impossible à la règle et au compas car π n'est pas un nombre algébrique.

Quadrature de la parabole

• Voir article détaillé : quadrature de la parabole

La parabole n'est pas une surface. La quadrature de la parabole consiste à déterminer l'aire de la surface comprise entre une corde et une portion de parabole.

Elle est résolue par Archimède (287-212 av. J.-C. ).C'est le premier exemple de calcul d'aire par la méthode d'exhaustion (l'erreur commise diminue de plus de 50% à chaque étape). Le résultat est connu de nos jours très facilement grâce au calcul de primitive:

L'aire sous la courbe d'équation y = x² entre les points a et b est

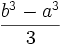
L'aire délimitée par cette même parabole et la corde est

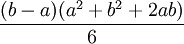
Si a et b sont opposés alors l'aire délimitée par la parabole et la corde est .

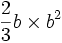Cette formule se généralise à toute parabole d'équation y = kx² , l'aire devenant .

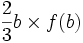Quadratures des fonctions de kx^m

Elles concernent le calcul de l'aire de la surface comprise entre l'axe des x, la courbe et la droite d'équation x = a (pour m > 0), ou bien l'aire de la surface comprise entre l'axe des x, la courbe, et située à droite de la droite d'équation x = a (pour m ≤ -2).

Elles sont mises au point par Fermat pour tout entier relatif différent de -1, ainsi que pour tout m rationnel positif. Il démontre que cette aire est toujours égale à

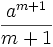
Quadrature de la cycloïde

La cycloïde est une courbe particulièrement étudiée par Galilée (1599). De nombreux mathématiciens ont cherché à calculer l'aire sous une arche de cycloïde. Galilée même a tenté une résolution expérimentale en découpant un cycloïde et en la pesant. La quadrature de la cycloïde est résolue presque simultanément par Roberval (1634) et Torricelli qui démontrent que l'aire sous une arche est égale à 3 fois l'aire du cercle qui génère la cycloïde.

Quadrature de l'hyperbole y = 1/x

C'est l'aire comprise entre la courbe, l'axe des abscisses et les droites d'équation x = a et x = 1.

Elle est découverte par Grégoire de Saint-Vincent (1647) qui met en évidence la propriété L(ab) = L(a) + L(b) si l'on appelle L(a) l'aire entre 1 et a, rangeant cette aire dans la famille de fonctions logarithmes. On sait aujourd'hui qu'il s'agit de la fonction logarithme neperien

Voir aussi

• Calcul numérique d'une intégrale
• Méthode de Romberg
• Méthodes de quadrature de Gauss
• Quadrature du carré

• Portail des mathématiques