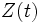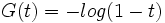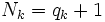Fonction Zeta Locale

Fonction Zeta Locale

Fonction zêta locale

En mathématiques et dans la théorie des nombres, une fonction zêta locale est une fonction génératrice

Z(t)\,

pour le nombre de solutions d'un ensemble d'équations définies sur un corps fini F, dans les extensions de corps 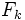F_k\, de F. L'analogie avec la fonction zêta de Riemann

\zeta(s)\,

vient de la considération de la dérivée logarithmique

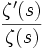\frac{\zeta'(s)}{\zeta(s)}\,.

Étant donné F, il existe, à un isomorphisme près, juste un corps 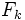F_k\, avec

[F_k : F] = k\,,

pour k = 1,2, ... . Étant donné un ensemble d'équations polynômiales - ou une variété algébrique V - définie sur F, nous pouvons compter le nombre

N_k\,

des solutions dans 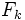F_k\,; et créer la fonction génératrice

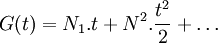G(t) = N_1.t + N^2.\frac{t^2}{2} + \ldots\,.

La définition correcte pour Z(t) est de rendre log Z égal à G, et donc

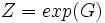Z = exp(G)\,;

Nous aurons Z(0) = 1 puisque G(0) = 0, et Z(t) est a priori une série de puissances formelles.

Exemples

Supposons que tous les 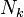N_k\, sont égaux à 1; ceci se produit par exemple, si nous démarrons avec une équation comme X = 0, c’est-à-dire que géométriquement, nous prenons pour V un point. Alors

G(t) = - log(1 - t)\,

est le développement d'un logarithme (pour |t| < 1). Dans ce cas, nous avons

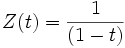Z(t) = \frac{1}{(1 - t)}\,.

Pour prendre quelque chose de plus intéressant, soit V la droite projective sur F. Si F possède q éléments, alors ceci a q + 1 points, incluant comme nous devons, le point à l'infini. Par conséquent, nous aurons

N_k = q_k + 1\,

et

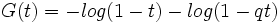G(t) = - log(1 - t) - log(1 - qt)\,,

pour |t| suffisamment petit.

Dans ce cas, nous avons

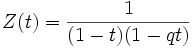Z(t) = \frac{1}{(1 - t)(1 - qt)}\,.

Le rapport entre les définitions de G et Z peut être expliqué de nombreuses manières. En pratique, cela rends Z une fonction rationnelle de t, quelque chose qui est intéressant même dans le cas où V est une courbe elliptique sur un corps fini.

C'est les fonctions Z qui sont conçues pour multiplier, pour obtenir les fonctions zêta globales. Celles-ci impliquent différents corps finis (par exemple la famille entière de corps Z/p.Z lorsque p parcours l'ensemble des nombres premiers. Dans ce rapport, la variable t subit la substitution par 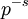p^{-s}\,, où s est la variable complexe traditionnellement utilisée dans les séries de Dirichlet.

Article détaillé : fonction zêta de Hasse-Weil.

.

Ceci explique aussi pourquoi la dérivée logarithmique conservant S est utilisée.

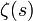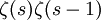Avec cet arrangement, les produits de Z dans les deux cas sortent comme \zeta(s)\, et \zeta(s)\zeta(s-1)\,.

Hypothèse de Riemann pour les courbes sur les corps finis

Pour les courbes projectives C sur F qui sont non-singulières, il peut être montré que

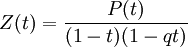Z(t) = \frac{P(t)}{(1 - t)(1 - qt)}\,,

avec P(t) un polynôme, de degré 2g où g est le genre de C. L'hypothèse de Riemann pour les courbes sur les corps finis établit que les racines de P ont pour valeurs absolues

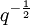q^{- \frac{1}{2}}\,,

où q = |F|.

Par exemple, pour le cas des courbes elliptiques où il existe deux racines, et il est facile de montrer que leur produit est 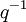q^{-1}\,. Le théorème de Hasse établit qu'elles ont la même valeur absolue; et ceci a des conséquences immédiates pour le nombre de points.

Weil a démontré ceci pour le cas général, aux environs de 1940 (Comptes Rendus note, avril 1940) : il passa beaucoup de temps, dans les années qui suivirent, à préparer la géométrie algébrique impliquée). Ceci l'a conduit aux conjectures de Weil générales, finalement démontrées une génération plus tard.

Article détaillé : cohomologie étale.

pour les formules de base de la théorie générale.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Fonction z%C3%AAta locale ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction Zeta Locale de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Fonction Zeta locale — Fonction zêta locale En mathématiques et dans la théorie des nombres, une fonction zêta locale est une fonction génératrice pour le nombre de solutions d un ensemble d équations définies sur un corps fini F, dans les extensions de corps de F. L… …   Wikipédia en Français

  • Fonction zeta locale — Fonction zêta locale En mathématiques et dans la théorie des nombres, une fonction zêta locale est une fonction génératrice pour le nombre de solutions d un ensemble d équations définies sur un corps fini F, dans les extensions de corps de F. L… …   Wikipédia en Français

  • Fonction zêta locale — En mathématiques et dans la théorie des nombres, une fonction zêta locale est une fonction génératrice pour le nombre de solutions d un ensemble d équations définies sur un corps fini F, dans les extensions de corps de F. L analogie avec la… …   Wikipédia en Français

  • Fonction Zeta — Fonction zêta Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La fonction zêta (d après la lettre grecque zêta, ou ζ) est le nom de nombreuses fonctions en mathématiques. La plus connue est la fonction… …   Wikipédia en Français

  • Fonction zeta — Fonction zêta Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La fonction zêta (d après la lettre grecque zêta, ou ζ) est le nom de nombreuses fonctions en mathématiques. La plus connue est la fonction… …   Wikipédia en Français

  • Fonction Zeta De Hasse-Weil — Fonction zêta de Hasse Weil En mathématiques, la fonction zêta de Hasse Weil attachée à une variété algébrique V définie sur un corps de nombres K est un des deux types les plus importants des fonctions L. De telles fonctions L sont appelées… …   Wikipédia en Français

  • Fonction zeta de Hasse-Weil — Fonction zêta de Hasse Weil En mathématiques, la fonction zêta de Hasse Weil attachée à une variété algébrique V définie sur un corps de nombres K est un des deux types les plus importants des fonctions L. De telles fonctions L sont appelées… …   Wikipédia en Français

  • Fonction zeta de hasse-weil — Fonction zêta de Hasse Weil En mathématiques, la fonction zêta de Hasse Weil attachée à une variété algébrique V définie sur un corps de nombres K est un des deux types les plus importants des fonctions L. De telles fonctions L sont appelées… …   Wikipédia en Français

  • Fonction zêta de Riemann — La fonction zêta de Riemann ζ(s) dans le plan complexe. La couleur d un point s code la valeur de ζ(s) : des couleurs vives indiquent des valeurs proches de 0 et la nuance indique l argument de la valeur. Le point blanc pour s = 1… …   Wikipédia en Français

  • Fonction zêta — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La fonction zêta (d après la lettre grecque zêta, ou ζ) est le nom de nombreuses fonctions en mathématiques. La plus connue est la fonction zêta de… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”