Cohomologie Galoisienne

Cohomologie Galoisienne

Cohomologie galoisienne

En mathématiques, la cohomologie galoisienne est l'étude de l'action d'un groupe de Galois sur certains groupes, par des méthodes cohomologiques. Elle permet d'obtenir des résultats à la fois sur le groupe de Galois agissant, et sur le groupe sur lequel il agit. En particulier, le groupe de Galois d'une extension de corps de nombres L/K agit naturellement par exemple sur le groupe multiplicatif 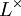L^\times, mais aussi sur le groupe des unités du corps L, ou sur son groupe des classes.

Le cadre naturel pour définir les complexes cohomologiques étudiés est plus abstrait que celui de la cohomologie galoisienne stricto sensu : voir cohomologie des groupes profinis.

En théorie algébrique des nombres

La formulation actuelle de la cohomologie galoisienne prend sa source dans les années 1950, avec les travaux de Claude Chevalley, qui permirent une nouvelle formulation, une formulation cohomologique, de la théorie des corps de classes, en particulier en évitant tout recours aux fonctions L. D'anciens résultats s'interprétèrent alors comme des résultats cohomologiques : le théorème 90 de Hilbert, datant du XIXe siècle, par exemple stipule l'annulation du premier groupe de cohomologie pour l'action d'un groupe de Galois cyclique sur le groupe multiplicatif du surcorps considéré ; et sa généralisation par Emmy Noether devient la généralisation de ce fait pour une extension finie. La théorie de Kummer s'interprète quant à elle comme un résultat de dualité.

Une question importante concernant la cohomologie galoisienne est celle de l'obtention d'un éventuel principe local-global. Les groupes de Chafarevitch, qui mesurent l'obstruction à un tel principe, sont encore mal compris, et constituent un thème de recherche important.

En géométrie algébrique

Les groupes de Chafarevitch, dans le cadre des courbes elliptiques, interviennent dans la formulation de la conjecture de Birch et Swinnerton-Dyer.

Références

Jean-Pierre Serre, Cohomologie galoisienne [détail des éditions]

(en) Jürgen Neukirch, Alexander Schmidt, Kay Wingberg Cohomology of number fields [détail des éditions]

Ce document provient de « Cohomologie galoisienne ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Cohomologie Galoisienne de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Cohomologie galoisienne — En mathématiques, la cohomologie galoisienne est l étude de l action d un groupe de Galois sur certains groupes, par des méthodes cohomologiques. Elle permet d obtenir des résultats à la fois sur le groupe de Galois agissant, et sur le groupe sur …   Wikipédia en Français

  • Cohomologie Des Groupes Profinis — La cohomologie des groupes profinis est une théorie cohomologique, reposant sur la théorie des groupes profinis. Elle consiste en un raffinement de la cohomologie des groupes classique, principalement par la prise en compte de la nature… …   Wikipédia en Français

  • Cohomologie des groupes profinis — La cohomologie des groupes profinis est une théorie cohomologique, reposant sur la théorie des groupes profinis. Elle consiste en un raffinement de la cohomologie des groupes classique, principalement par la prise en compte de la nature… …   Wikipédia en Français

  • Cohomologie — Homologie et cohomologie Pour les articles homonymes, voir Homologie. L homologie est une technique générale en mathématiques qui sert à mesurer l obstruction qu ont certaines suites de morphismes à être exactes. Elle intervient dans de nombreux… …   Wikipédia en Français

  • Homologie et cohomologie — Pour les articles homonymes, voir Homologie. L homologie est une technique générale en mathématiques qui sert à mesurer l obstruction qu ont certaines suites de morphismes à être exactes. Elle intervient dans de nombreux domaines comme l algèbre …   Wikipédia en Français

  • Homologie Et Cohomologie — Pour les articles homonymes, voir Homologie. L homologie est une technique générale en mathématiques qui sert à mesurer l obstruction qu ont certaines suites de morphismes à être exactes. Elle intervient dans de nombreux domaines comme l algèbre …   Wikipédia en Français

  • Representation galoisienne — Représentation galoisienne La théorie des représentations galoisiennes est l application naturelle de la théorie des représentations à la théorie algébrique des nombres. Un module galoisien est un module sur lequel agit un groupe de Galois G. Ces …   Wikipédia en Français

  • Représentation galoisienne — La théorie des représentations galoisiennes est l application naturelle de la théorie des représentations à la théorie algébrique des nombres. Un module galoisien est un module sur lequel agit un groupe de Galois G. Ces modules seront par exemple …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Algèbre homologique — Homologie et cohomologie Pour les articles homonymes, voir Homologie. L homologie est une technique générale en mathématiques qui sert à mesurer l obstruction qu ont certaines suites de morphismes à être exactes. Elle intervient dans de nombreux… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”