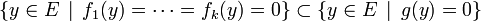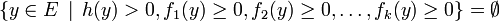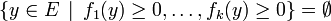- Lemme de farkas
-
Lemme de Farkas
Le lemme de Farkas est un résultat de géométrie convexe essentiel en programmation linéaire où il fonde la théorie de la dualité pour les programmes linéaires, ainsi qu'en théorie des jeux. Il intervient dans la preuve du théorème de Karush-Kuhn-Tucker en programmation non linéaire.
Il affirme, avec quelques précautions techniques nécessaires, qu'étant donnée une famille d'inéquations linéaires (ou affines) dans un espace vectoriel réel de dimension finie, il n'y a pas d'autres conséquences à en déduire que celles qui se déduisent de façon évidente.
On peut donner plusieurs versions du lemme de Farkas, toutes essentiellement équivalentes les unes aux autres.
Ce lemme est un des « théorèmes de l'alternative », qui fournissent pour un système d'inéquations linéaires une condition nécessaire et suffisante d'existence de solution, qui peut s'exprimer comme inexistence de solutions pour un autre problème de forme voisine.
Sommaire
Historique
Ce lemme a été historiquement démontré pour la première fois par Gyula Farkas en 1902 (Über die Theorie der Einfachen Ungleichungen, Journal für die Reine und Angewandte Mathematik 124, p1-27) avec une formulation différente. La formulation matricielle est due à Albert William Tucker dans les années 1950.
La version du lemme en géométrie vectorielle
Avant de donner l'énoncé du lemme de Farkas, commençons par rappeler un résultat sur les équations linéaires, suffisamment simple pour ne pas bénéficier d'une dénomination particulière, et dont le lemme de Farkas est la généralisation aux inégalités.
Proposition — Soit
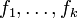 et g des formes linéaires sur un espace vectoriel de dimension finie E. Alors :
et g des formes linéaires sur un espace vectoriel de dimension finie E. Alors :si et seulement si
- g appartient à l'espace vectoriel formé des combinaisons linéaires de
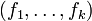 .
.
Dit autrement : étant donné un sous-espace vectoriel de E décrit par une liste d'équations cartésiennes, toute autre équation valable sur ce sous-espace s'obtient en combinant de façon immédiate les équations initialement fournies.
Le lemme de Farkas est le résultat analogue pour des systèmes d'inéquations :
Lemme de Farkas, version vectorielle — Soit
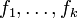 et g des formes linéaires sur un espace vectoriel réel de dimension finie E. Alors :
et g des formes linéaires sur un espace vectoriel réel de dimension finie E. Alors :si et seulement si
- g appartient à l'ensemble des combinaisons linéaires à coefficients positifs ou nuls de
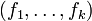 .
.
Une des preuves passe par l'étape suivante cruciale, qui est aussi parfois appelée lemme de Farkas :
Lemme de Farkas, version topologique — Soit
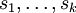 des éléments d'un espace vectoriel réel de dimension finie E. L'ensemble des combinaisons linéaires à coefficients positifs ou nuls de
des éléments d'un espace vectoriel réel de dimension finie E. L'ensemble des combinaisons linéaires à coefficients positifs ou nuls de 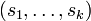 est fermé dans E.
est fermé dans E.La version matricielle du lemme
On rappelle que B étant une matrice de réels, on note
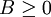 lorsque tous les coefficients de B sont positifs ou nuls. La notation BT désigne la transposée de B.
lorsque tous les coefficients de B sont positifs ou nuls. La notation BT désigne la transposée de B.La version matricielle du lemme est la suivante :
Lemme de Farkas, version matricielle — Soit A une matrice de réels de taille (n,k) et b un vecteur-colonne avec n entrées, alors un et un seul des systèmes linéaires suivants a une solution :
- le système
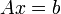 pour x vecteur-colonne à k entrées vérifiant par ailleurs
pour x vecteur-colonne à k entrées vérifiant par ailleurs 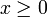 ;
;
- ou le système
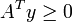 pour
pour 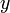 vecteur-colonne à n entrées vérifiant par ailleurs
vecteur-colonne à n entrées vérifiant par ailleurs 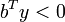 .
.
La vérification est sans difficulté aucune, une fois qu'on a passé l'obstacle de raccrocher les matrices de cet énoncé aux objets géométriques de l'énoncé précédent.
VérificationPour chaque colonne Cj de A (
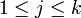 ), notons fj la forme linéaire définie sur
), notons fj la forme linéaire définie sur 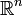 par
par 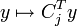 ; notons par ailleurs g la forme linéaire
; notons par ailleurs g la forme linéaire 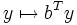 .
.L'existence d'une solution pour la première branche de l'alternative, c'est l'existence d'un k-uplet
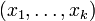 de nombres positifs ou nuls tels que
de nombres positifs ou nuls tels que 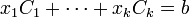 , autrement dit c'est la possibilité d'écrire g comme combinaison linéaire à coefficients positifs des fj.
, autrement dit c'est la possibilité d'écrire g comme combinaison linéaire à coefficients positifs des fj.L'existence d'une solution pour la deuxième branche de l'alternative, c'est l'existence d'un y qui soit dans
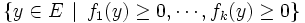 mais qui ne soit pas dans
mais qui ne soit pas dans 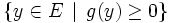 .
.L'équivalence annoncée par le théorème de Farkas garantit donc précisément qu'un et un seul des deux systèmes a une solution.
Le lemme de Farkas comme critère d'inconsistance
On dira qu'un système d'inéquations est inconsistant lorsqu'il n'a aucune solution. Si on revient à la version du théorème pour les équations linéaires, dire que
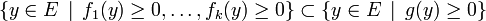 c'est la même chose que de dire que l'ensemble
c'est la même chose que de dire que l'ensemble 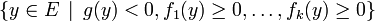 est vide : c'est un énoncé d'inconsistance. En notant h=-g, on a donc la variante suivante :
est vide : c'est un énoncé d'inconsistance. En notant h=-g, on a donc la variante suivante :Lemme de Farkas, critère vectoriel d'inconsistance — Soit
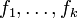 et h des formes linéaires sur un espace vectoriel réel de dimension finie E. Alors :
et h des formes linéaires sur un espace vectoriel réel de dimension finie E. Alors :si et seulement si
- − h appartient à l'ensemble des combinaisons linéaires à coefficients positifs ou nuls de
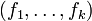 .
.
Par ce critère vectoriel d'inconsistance, on obtient facilement un critère d'inconsistance pour les systèmes affines directement apparenté, et d'aspect un peu plus simple :
Lemme de Farkas, critère affine d'inconsistance — Soit
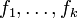 des formes affines sur un espace affine réel de dimension finie E.
des formes affines sur un espace affine réel de dimension finie E.Alors :
si et seulement si
- − 1 appartient à l'ensemble des combinaisons linéaires à coefficients positifs ou nuls de
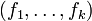 .
.
On voit de nouveau là très nettement l'idée sous-jacente à tous ces énoncés, appliquée dans le cas de l'inconsistance : un système inconsistant implique (au sens du calcu propositionnel) l'inéquation absurde
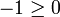 ; le lemme de Farkas assure dès lors qu'elle peut en être déduite non seulement par des raisonnements plus ou moins compliqués mais aussi tout simplement par combinaisons des équations du système.Démonstration
; le lemme de Farkas assure dès lors qu'elle peut en être déduite non seulement par des raisonnements plus ou moins compliqués mais aussi tout simplement par combinaisons des équations du système.DémonstrationL'implication montante est évidente, montrons l'autre. On suppose donc
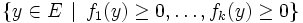 vide.
vide.Introduisons un espace vectoriel
 dans lequel E est un sous-espace affine de codimension 1 ne passant pas par l'origine. Toute forme affine sur E se prolonge d'une façon unique en une forme linéaire sur
dans lequel E est un sous-espace affine de codimension 1 ne passant pas par l'origine. Toute forme affine sur E se prolonge d'une façon unique en une forme linéaire sur 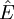 . Notons
. Notons 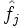 le prolongement linéaire de fj (
le prolongement linéaire de fj (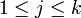 ) et
) et 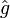 le prolongement de la constante − 1, de sorte que E a pour équation
le prolongement de la constante − 1, de sorte que E a pour équation 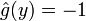 dans
dans 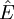 .
.L'hypothèse revient à dire que si un point y de
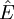 vérifie les conditions
vérifie les conditions  , il ne vérifie pas la condition
, il ne vérifie pas la condition 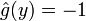 . En jouant avec les homothéties de rapport strictement positif, il est immédiat qu'il ne peut pas non plus vérifier
. En jouant avec les homothéties de rapport strictement positif, il est immédiat qu'il ne peut pas non plus vérifier 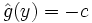 pour un autre niveau strictement négatif. En d'autres termes l'ensemble
pour un autre niveau strictement négatif. En d'autres termes l'ensemble 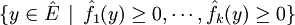 est inclus dans l'ensemble
est inclus dans l'ensemble 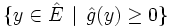 . On applique alors Farkas et on en déduit que
. On applique alors Farkas et on en déduit que 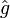 est une combinaison linéaire à coefficients positifs des
est une combinaison linéaire à coefficients positifs des 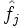 . Il n'y a plus qu'à restreindre à E la relation obtenue.
. Il n'y a plus qu'à restreindre à E la relation obtenue.Déduction d'inéquations en géométrie affine
La simple reproduction du résultat écrit plus haut en géométrie vectorielle serait inexacte en géométrie affine. L'énoncé est en effet faux pour les systèmes d'inéquations inconsistants. Donnons tout de suite un exemple : dans
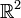 où on note (u,v) le point courant, soit le système formé des deux inéquations :
où on note (u,v) le point courant, soit le système formé des deux inéquations : 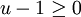 et
et 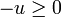 . Ce système est inconsistant, faux en tout point, et implique donc (au sens précis de "implique" en calcul propositionnel) n'importe quelle inéquation, par exemple l'inéquation
. Ce système est inconsistant, faux en tout point, et implique donc (au sens précis de "implique" en calcul propositionnel) n'importe quelle inéquation, par exemple l'inéquation 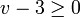 . Pourtant il n'est bien sûr pas question de produire celle-ci par des manipulations algébriques simples à partir du système initial.
. Pourtant il n'est bien sûr pas question de produire celle-ci par des manipulations algébriques simples à partir du système initial.Un énoncé général nécessite ainsi une hypothèse supplémentaire de consistance du système.
« Lemme de Farkas généralisé » — Soit
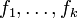 et g des formes affines sur un espace vectoriel affine de dimension finie E. On suppose l'ensemble
et g des formes affines sur un espace vectoriel affine de dimension finie E. On suppose l'ensemble 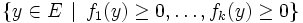 non vide. Alors :
non vide. Alors :si et seulement si
- g est somme d'une combinaison linéaire à coefficients positifs ou nuls de
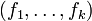 et d'une constante positive ou nulle.
et d'une constante positive ou nulle.
DémonstrationComme dans la démonstration précédente l'implication montante est évidente. On montre l'autre, en supposant tout d'abord que
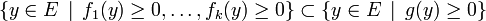 . On note de nouveau
. On note de nouveau 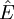 un espace vectoriel dont E est un sous-espace affine de codimension 1 ne passant pas par l'origine,
un espace vectoriel dont E est un sous-espace affine de codimension 1 ne passant pas par l'origine, 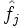 l'extension linéaire de fj à cet espace, et naturellement
l'extension linéaire de fj à cet espace, et naturellement 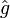 l'extension linéaire de g à cet espace. On note cette fois h la constante valant 1 sur E et
l'extension linéaire de g à cet espace. On note cette fois h la constante valant 1 sur E et 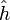 son extension à
son extension à 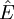 .
.On vérifie ensuite que :
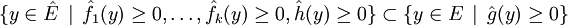 :
:
pour un point y de l'ensemble de gauche, on discute selon la valeur de h(y) qui est supposé positif ou nul :
- si h(y) = 1, c'est qu'on est dans E et l'appartenance à l'ensemble de droite est assurée par l'hypothèse ;
- plus généralement, si h(y) > 0, on se ramène au cas précédent par homothétie de rapport strictement positif ;
- si h(y) = 0 on a besoin de l'hypothèse de consistance du système initial. On prend un point auxiliaire
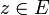 vérifiant ce système, et on se dirige de z vers y le long du segment [z,y[ : tout au long du voyage, les
vérifiant ce système, et on se dirige de z vers y le long du segment [z,y[ : tout au long du voyage, les 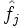 gardent toutes des valeurs positives ou nulles tandis que
gardent toutes des valeurs positives ou nulles tandis que 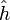 reste à valeurs strictement positives ; le cas précédent assure donc que g est lui aussi à valeurs positives ou nulles sur le segment. On conclut alors que
reste à valeurs strictement positives ; le cas précédent assure donc que g est lui aussi à valeurs positives ou nulles sur le segment. On conclut alors que 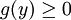 par passage à la limite.
par passage à la limite.
Il ne reste plus qu'à appliquer le lemme de Farkas dans sa version vectorielle pour conclure que
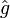 est une combinaison linéaire à coefficients positifs des
est une combinaison linéaire à coefficients positifs des 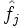 et de
et de 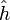 ; on termine en restreignant cette conclusion à E.
; on termine en restreignant cette conclusion à E.Références
L'article, à l'exception de la section historique, est une adaptation assez distanciée des pages 58-62 de Fundamentals of convex analysis, Jean-Baptiste Hiriart-Urruty et Claude Lemaréchal, coll. « Grundlehren Text Editions », Springer, 2001 (ISBN 3540422056), à la lumière de l'entrée du blog de Terence Tao du 30 novembre 2007, disponible en ligne.
Littérature
- Julius Farkas. "Über die Theorie der Einfachen Ungleichungen". Journal für die Reine und Angewandte Mathematik 124. p1-27
- Portail des mathématiques
Catégories : Optimisation | Lemme de mathématiques | Géométrie convexe
Wikimedia Foundation. 2010.