Intégrale de Fresnel

Pour les articles homonymes, voir Fresnel.

L'intégrale de Fresnel est une intégrale impropre introduite par le physicien français Augustin Fresnel.

Sommaire

1 Formule de Fresnel
2 Définition
3 Calcul de l'intégrale de Fresnel
- 3.1 Par une intégrale à paramètre
- 3.2 Par intégration complexe
4 Articles connexes

Formule de Fresnel

Les fonctions S(x) et C(x) non normalisées

$\int_{0}^{+\infty} \cos(x^2)\;\mathrm{d}x = \int_{0}^{+\infty} \sin(x^2)\;\mathrm{d}x = \frac{1}{2}\sqrt{\frac{\pi}{2}}$

On en déduit l'intégrale de Fresnel complexe :

$\int_{0}^{+\infty} e^{\pm i x^2} \mathrm{d}x = \int_{0}^{+\infty} \cos(x^2)\mathrm{d}x \pm i \int_{0}^{+\infty} \sin(x^2)\mathrm{d}x = \frac{1}{2}\sqrt{\frac{\pi}{2}}( 1 \pm i ) = \frac{\sqrt{\pi}}{2} e^{\pm i\frac{\pi}{4}}$

Définition

Les fonctions S(x) et C(x) normalisées

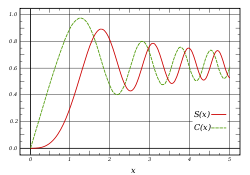
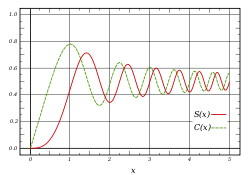
Les fonctions de Fresnel sont définies par les intégrales et développement en série entière associés :

$S(x)=\int_0^x \sin(t^2)\,\mathrm{d}t=\sum_{n=0}^{\infin}(-1)^n\frac{x^{4n+3}}{(2n+1)!(4n+3)},$

$C(x)=\int_0^x \cos(t^2)\,\mathrm{d}t=\sum_{n=0}^{\infin}(-1)^n\frac{x^{4n+1}}{(2n)!(4n+1)}.$

Ces fonctions sont parfois définies avec l'argument $\frac{\pi}{2}t^2$ dans les intégrales définissant $S (x)$ et $C (x)$ . Les intégrales sont alors multipliées par $\sqrt{\frac{2}{\pi}}$ et les intégrandes sont divisés par x.

La formule de Fresnel vue précédemment est donc la limite en $+\infty$ des deux fonctions $S$ et $C$ non normalisées.

Calcul de l'intégrale de Fresnel

Par une intégrale à paramètre

Considérons pour tout réel $t$ la fonction de ℝ⁺ dans ℂ définie par

$u\mapsto {\mathrm e^{-(u^2+i)t^2}\over u^2+i}.$

Cette fonction est intégrable, car continue sur ℝ⁺ et majorée en module par $u\mapsto\displaystyle\tfrac1{u^2}$ , qui est intégrable en +∞.

Il est donc possible de poser $f$ , la fonction définie pour tout $t$ par l'intégrale à paramètre suivante :

$f(t)=\int_0^{+\infty}\frac{\mathrm e^{-(u^2+i)t^2}}{u^2+i}~\mathrm du.$

On montre que $f$ est continue sur $ℝ$ et nulle à l'infini, et qu'elle est de classe $C 1$ sur $ℝ +*$ avec

$\forall t\in\R^{+*},~f'(t)=-2t\mathrm e^{-it^2}\int_0^{+\infty}\mathrm e^{-u^2t^2}\mathrm du.$

Démonstration

On applique le théorème de convergence dominée.

Continuité sur ℝ et nullité à l'infini
- Pour tout $u \in ℝ +*$ , la fonction $\R\rightarrow\C,\ t\mapsto {\mathrm e^{-(u^2+i)t^2}\over u^2+i}$ est continue et nulle à l'infini.
- Pour tout réel t, la fonction $\R^+\rightarrow\C,\ u\mapsto {\mathrm e^{-(u^2+i)t^2}\over u^2+i}$ est continue donc mesurable.
- Condition de domination : $\forall (t,u)\in\R\times\R^+,~\left|{{\mathrm e^{-(u^2+i)t^2}}\over{u^2+i}}\right|\le\frac1{\sqrt{1+u^4}}$ et la fonction $u\mapsto\displaystyle\tfrac1{\sqrt{1+u^4}}$ est intégrable sur $ℝ +$ .
- Conclusion : $f$ est continue sur $ℝ$ et nulle à l'infini.
Classe C¹ sur ℝ^+* et valeur de la dérivée.
- Pour tout $u \in ℝ +$ , la fonction $\R^{+*}\rightarrow\C,\ t\mapsto {\mathrm e^{-(u^2+i)t^2}\over u^2+i}$ est dérivable et sa dérivée, $\R^{+*}\rightarrow\C,\ t\mapsto-2t\exp {[-(u^2+i)t^2]},$ est continue.
- Pour tout $t \in ℝ +*$ , la fonction $\R^+\rightarrow\C,\ u\mapsto-2t\exp {[-(u^2+i)t^2]}$ est mesurable.
- Condition de domination : confinons le paramètre $t$ à l'intervalle $] a, b [$ avec $0 < a < b$ . $\forall (t,u)\in]a,b[\times\R^+,~\left|-2t\exp {[-(u^2+i)t^2]}\right|\le2b~\mathrm e^{-u^2a^2}$ et la fonction $u\mapsto 2b~\mathrm e^{-u^2a^2}$ est intégrable sur $ℝ +$ .
- Conclusion : $f$ est de classe $C 1$ sur $ℝ +*$ et

$\forall t\in\R^{+*},~f'(t)=-2t\mathrm e^{-it^2}\int_0^{+\infty}\mathrm e^{-u^2t^2}\mathrm du.$

En simplifiant l'expression de $f'~$ et en l'intégrant de 0 à +∞, on en déduit que

$\int_0^{+\infty}\mathrm e^{-it^2}~\mathrm dt=\frac1{\sqrt\pi}\int_0^{+\infty}\frac1{u^2+i}~\mathrm du.$

Démonstration

En opérant un changement de variable linéaire par la fonction $ℝ + \to ℝ +, u \mapsto u\cdott = v$ , on aboutit immédiatement à, pour tout $t \in ℝ +*$ :

$f'(t)=-2\mathrm e^{-it^2}\int_0^{+\infty}\mathrm e^{-v^2}~\mathrm dv.$

L'intégrale définie est ici bien connue (voir l'article sur l'intégrale de Gauss) et vaut $\tfrac{\sqrt{\pi}}{2}$ . Ainsi, on a une expression plus simple de la dérivée de $f$ :

$f'(t)=-\sqrt{\pi}\mathrm e^{-it^2}$ .

Par conséquent :

$0-\int_0^{+\infty}{1\over u^2+i}~\mathrm du=\left(\lim_{t\to+\infty}f(t)\right)-f(0)=\int_0^{+\infty}f'(t)~\mathrm dt=-\sqrt\pi\int_0^{+\infty}\mathrm e^{-it^2}~\mathrm dt.$

On se sert alors d'une intégrale classique :

$\int_0^{+\infty}{1\over u^4+1}~\mathrm du=\int_0^{+\infty}{u^2\over u^4+1}~\mathrm du$

et de l'expression $\tfrac1{u^2+i}$ sous la forme $\tfrac{u^2-i}{u^4+1}$ pour en déduire que

$\int_0^{+\infty}\mathrm e^{-it^2}~\mathrm dt =\frac12\sqrt{\frac\pi2}(1-i)$ .

Il reste à prendre les parties réelle et imaginaire pour conclure que :

$\int_0^{+\infty}\cos(-t^2)~\mathrm dt=\Re \mathfrak e\left(\int_0^{+\infty}\mathrm e^{-it^2}~\mathrm dt\right) =\frac12\sqrt{\frac\pi2}$

$-\int_0^{+\infty}\sin(t^2)~\mathrm dt=\int_0^{+\infty}\sin(-t^2)~\mathrm dt=\Im \mathfrak{m}\left(\int_0^{+\infty}\mathrm e^{-it^2}~\mathrm dt\right)=-\frac12\sqrt{\frac\pi2}$ .

Par intégration complexe

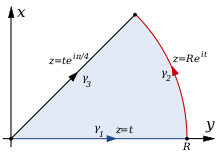
Il est aussi possible d'intégrer $f (z) = exp( - z 2)$ sur les bornes du triangle $T R$ de sommets $0, ~R, ~(1+i)~ R$ puis de faire tendre $R$ vers l'infini.

Contour utilisé pour le calcul

$\displaystyle\oint f(z)\,\text{d}z=\underbrace{\int_0^R \text{e}^{-t^2}\,\text{d}t}_{I_1(R)}+\underbrace{\int_0^{\pi/4} iR\,\text{e}^{it}\,\text{e}^{-R^2\exp(2it)}\,\text{d}t}_{I_2(R)}-\underbrace{\int_0^R \text{e}^{i\frac{\pi}{4}}\,\text{e}^{-it^2}\,\text{d}t}_{I_3(R)}$

Intéressons nous d'abord à $I 2$ .

$|I_2(R)|\leq \displaystyle\int_0^{\pi/4}R\,\text{e}^{-R^2\cos(2t)}\,\text{d}t = \int_0^{\pi/2} \dfrac{R}{2}\,\text{e}^{-R^2\cos u}\,\text{d}u$

après un changement de variable $u = 2 t$ . Or, sur $\left[0,\dfrac{\pi}{2}\right]$ , la concavité de $cos$ donne

$\forall u\in\left[0,\dfrac{\pi}{2}\right],\quad 1-\dfrac{2}{\pi}u\leq\cos u\leq 1$

donc

$\forall u\in\left[0,\dfrac{\pi}{2}\right],\quad \text{e}^{-R^2\cos u}\leq \,\text{e}^{R^2\left(\frac{2}{\pi}u-1\right)}$

donc

$\displaystyle\int_0^{\pi/2}\dfrac{R}{2}\,\text{e}^{-R^2\cos u}\,\text{d}u\leq \dfrac{\pi}{4R}\left(1-\text{e}^{-R^2}\right)$

Le théorème des gendarmes donne ainsi $\displaystyle\lim_{R\rightarrow +\infty}I_2(R)=0$ . Grâce au résultat de l'intégrale de Gauss, $\displaystyle\lim_{R\rightarrow +\infty}I_1(R)=\dfrac{\sqrt{\pi}}{2}$ . De plus, $\displaystyle\lim_{R\rightarrow +\infty}I_3(R)=\dfrac{1+i}{\sqrt{2}}\displaystyle\int_0^{+\infty} \text{e}^{-it^2}\,\text{d}t$ .