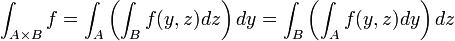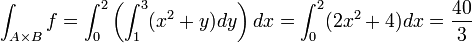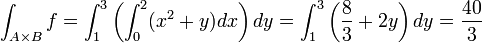- Intégrale à paramètre
-
Intégrale paramétrique
En mathématiques, une intégrale paramétrique (également appelée intégrale à paramètre) est une fonction définie à partir de l'intégration d'une fonction de plusieurs variables sur un ensemble fixe par rapport à une partie des variables seulement. Une classe importante d'exemples est l'ensemble des transformées dont par exemple la transformée de Fourier.
Sommaire
Exemples
Transformée de Fourier
Article détaillé : transformée de Fourier.Soit f une fonction de
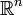 dans
dans 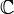 , L-intégrable sur
, L-intégrable sur 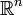 , la transformée de Fourier de f est la fonction de
, la transformée de Fourier de f est la fonction de 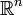 dans
dans 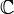 définie par la formule suivante :
définie par la formule suivante :où
 désigne le produit scalaire usuel.
désigne le produit scalaire usuel.Fonction gamma d'Euler
Article détaillé : fonction gamma.La fonction gamma d'Euler est définie pour chaque
![x\in ]0,\infty[](/pictures/frwiki/50/289ae433c8c50e4ee7abea4410357881.png) par la formule suivante :
par la formule suivante :Potentiel du champ de gravitation
Article détaillé : énergie potentielle gravitationnelle.Le potentiel du champ de gravitation créé par un corps matériel M de densité variable ρ en un point
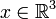 extérieur à M est donné par la formule suivante
extérieur à M est donné par la formule suivanteoù G désigne la constante de gravitation et
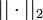 la norme euclidienne.
la norme euclidienne.Définition formelle
Si
 et
et  sont des entiers tels que q + s = n, on écrira
sont des entiers tels que q + s = n, on écrira 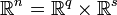 avec x = (y,z) pour chaque élément
avec x = (y,z) pour chaque élément 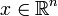 .
.Soit f une fonction de
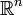 dans
dans 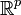 , A une partie de
, A une partie de  et B une partie de
et B une partie de  . Si,
. Si, 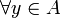 , la fonction
, la fonction 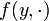 de
de  dans
dans 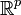 est intégrable sur B, alors l'application F de A dans
est intégrable sur B, alors l'application F de A dans 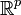 définie par :
définie par :F(y) = ∫ f(y,z)dz B est appelée une intégrale paramétrique.
Existence d'une limite
Soit
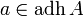 et si les conditions suivantes sont satisfaites :
et si les conditions suivantes sont satisfaites :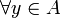 , la fonction
, la fonction 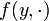 est intégrable sur B ,
est intégrable sur B ,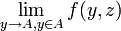 existe pour presque tout
existe pour presque tout 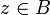 ,
,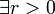 et des fonctions réelles g et h intégrables sur B telles que
et des fonctions réelles g et h intégrables sur B telles que ![\forall y\in A\cap B_{\infty}[a;r]](/pictures/frwiki/51/3f8f7b378b97dbc7d3fd65ea2dd1f372.png) et pour presque tout
et pour presque tout 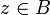 , on ait
, on ait
alors la fonction
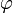 définie presque partout sur B par
définie presque partout sur B parest intégrable sur B et
soit encore :
Remarque, la notation
![B_{\infty}[a;r]](/pictures/frwiki/50/28e79bc2e8d831d71463d7a549d3a5f5.png) tient pour la boule fermée de centre a et de rayon r pour la norme infinie.Démonstration
tient pour la boule fermée de centre a et de rayon r pour la norme infinie.DémonstrationSoit
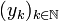 une suite dans
une suite dans ![A\cap B_{\infty}[a;r]](/pictures/frwiki/97/a76f0be04303e0192a55e336b474cc3b.png) qui converge vers a (par compacité une telle suite existe). La suite
qui converge vers a (par compacité une telle suite existe). La suite 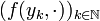 de fonctions intégrables sur B converge ponctuellement presque partout sur B vers
de fonctions intégrables sur B converge ponctuellement presque partout sur B vers 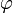 et on a par la troisième hypothèse :
et on a par la troisième hypothèse :pour tout
 et pour presque tout
et pour presque tout 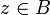 . Le théorème de convergence majorée et minorée de Lebesgue entraîne alors l'intégrabilité de
. Le théorème de convergence majorée et minorée de Lebesgue entraîne alors l'intégrabilité de 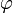 sur B et les relations
sur B et les relationsContinuité
Continuité locale : si l'on remplace la deuxième hypothèse du résultat précédent par une hypothèse de continuité de
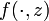 en
en 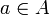 pour presque tout
pour presque tout 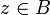 , on déduit du résultat précédent la continuité de F en a.
, on déduit du résultat précédent la continuité de F en a.Continuité globale : par conséquent, si f est continue sur
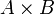 , que A est ouvert et B est fermé et borné, alors F est continue sur A.Démonstration
, que A est ouvert et B est fermé et borné, alors F est continue sur A.DémonstrationPar hypothèse,
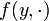 est continue sur B, et donc intégrable sur B pour chaque
est continue sur B, et donc intégrable sur B pour chaque 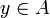 . Par ailleurs, on a aussi que
. Par ailleurs, on a aussi que 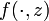 est continue sur A pour chaque
est continue sur A pour chaque 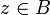 . Si
. Si 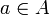 , il existe r > 0 tel que
, il existe r > 0 tel que ![B_{\infty}[a;r]](/pictures/frwiki/50/28e79bc2e8d831d71463d7a549d3a5f5.png) soit inclue dans A (qui est ouvert) et dès lors, par continuité de f, il existe une constante positive M telle que sur
soit inclue dans A (qui est ouvert) et dès lors, par continuité de f, il existe une constante positive M telle que sur ![B_{\infty}[a;r]\times B](/pictures/frwiki/97/a3a92c3108544c6746d170fb5335cdb8.png) , on ait :
, on ait :il suffit donc de prendre g = − M = − h dans la proposition précédente.
Règle de Leibniz de dérivation sous le signe d'intégration
Etude locale
Supposons que
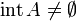 et que les trois conditions suivantes soient satisfaites :
et que les trois conditions suivantes soient satisfaites :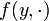 est intégrable sur B pour chaque
est intégrable sur B pour chaque 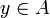
- Il existe un entier
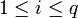 , un point
, un point  et un réel r > 0 tels que
et un réel r > 0 tels que ![B_{\infty}[a;r]\subset A](/pictures/frwiki/53/54041cfc35e1cbcf49d6d26859733f32.png) et tels que
et tels que 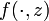 possède pour presque tout
possède pour presque tout 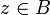 une dérivée partielle par rapport à yi en chaque point
une dérivée partielle par rapport à yi en chaque point ![y\in B_{\infty}[a;r]](/pictures/frwiki/51/33f4e2a2ff29a731f06136220c3a5dd5.png) .
. - Il existe deux fonctions réelles g et h intégrables sur B telles que, pour tout
![y\in B_{\infty}[a;r]](/pictures/frwiki/51/33f4e2a2ff29a731f06136220c3a5dd5.png) et presque tout
et presque tout 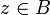 , on ait :
, on ait :
Alors, l'intégrale paramétrique F possède en a une dérivée partielle par rapport à yi. Par ailleurs,
 est intégrable sur B et :
est intégrable sur B et :Soit encore :
DémonstrationSoit ψ la fonction définie sur
![([-r, r]\backslash\{0\}) \times B](/pictures/frwiki/98/b7cada8e1aec0b3c16cdb1776f7f4ec9.png) par le quotient différentiel
par le quotient différentieloù
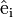 désigne le vecteur de base correspondant à la variable yi. On a que
désigne le vecteur de base correspondant à la variable yi. On a que 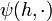 est intégrable sur B pour chaque
est intégrable sur B pour chaque ![h\in [-r, r]\backslash\{0\}](/pictures/frwiki/53/5a6a57a8bb9e5d9ee2aa487533ca7c14.png) et on a :
et on a :pour presque tout
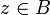 . En outre, en appliquant le théorème des accroissements finis, on a pour chaque h, un h' tel que :
. En outre, en appliquant le théorème des accroissements finis, on a pour chaque h, un h' tel que :avec 0 < | h' | < | h | . On a donc :
soit encore en utilisant la troisième hypothèse :
par conséquent en utilisant la proposition relative à la limite d'une intégrale paramétrique, on a que
 est intégrable sur B et :
est intégrable sur B et :or on a que :
ce qui est égal à :
Par conséquent,
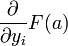 existe et vaut
existe et vaut 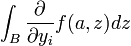 .
.Etude globale
Si A est ouvert, B est fermé borné et s'il existe
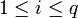 tel que, pour chaque
tel que, pour chaque  , f possède une dérivée partielle par rapport à yi et si
, f possède une dérivée partielle par rapport à yi et si 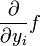 est une fonction continue sur
est une fonction continue sur 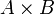 , alors F possède en chaque point
, alors F possède en chaque point 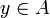 une dérivée partielle par rapport à yi, la fonction
une dérivée partielle par rapport à yi, la fonction  est continue sur A et, pour tout
est continue sur A et, pour tout 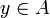 , on a :Démonstration
, on a :DémonstrationSoit
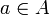 , il existe r > 0 tel que
, il existe r > 0 tel que ![B_\infty[a; r]\subset A](/pictures/frwiki/102/fb917a4a50e152de9c67002454416352.png) . Pour chaque
. Pour chaque ![y \in B_\infty[a;r]\times B](/pictures/frwiki/99/c5013285b9be47e6552590690d838145.png) , la fonction
, la fonction 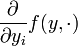 est continue, et donc intégrable, sur B et, par continuité, il existe une constante positive M telle que sur
est continue, et donc intégrable, sur B et, par continuité, il existe une constante positive M telle que sur ![B_\infty[a;r]\times B](/pictures/frwiki/50/20008f43264f8f16b4c758a4e07b9d0c.png) on ait :
on ait :les trois conditions de la règle de Leibniz locale sont donc satisfaites et on peut l'appliquer partout. La continuité de
 est déduite de la proposition sur la continuité globale d'une intégrale paramétrique.
est déduite de la proposition sur la continuité globale d'une intégrale paramétrique.Forme générale unidimensionnelle
Le résultat suivant peut être vu comme une généralisation du théorème fondamental de l'analyse et peut s'avérer utile dans le calcul de certaines intégrales réelles.
Soit f une fonction continue de
 dans
dans  et possédant une dérivée partielle continue sur
et possédant une dérivée partielle continue sur  par rapport à la première variable. Soient a et b deux fonctions dérivables de
par rapport à la première variable. Soient a et b deux fonctions dérivables de  dans
dans  , si F est l'intégrale paramétrique définie par :
, si F est l'intégrale paramétrique définie par :on montre que F est dérivable sur tout
 et que
et queRemarque : on retrouve bien le théorème fondamental de l'analyse en posant a(y) = a et b(y) = b.
DémonstrationSoit H l'application de
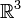 dans
dans  définie par :
définie par :et qui est donc telle que F(y) = H(a(y),b(y),y). Le théorème de dérivation des fonctions composées nous donne que :
du théorème fondamental de l'analyse, on a que :
et
finalement, en appliquant la règle de Leibniz pour le dernier terme, on a :
en mettant ensemble les trois dernières relations on retrouve l'identité.
Exemples
Calcul d'intégrale 1
Voici une des nombreuses applications possibles de la forme générale unidimensionnelle avec des bornes constantes. On considère l'intégrale de Gauss avec a > 0 :
on peut en déduire, en appliquant l'identité que :
DémonstrationComme les bornes sont des constantes, l'identité devient :
de l'autre côté on a :
en assemblant les deux derniers résultats, on retrouve la formule indiquée.
Remarque, on peut étendre le résultat à toute intégrale ayant pour intégrande x2nexp( − ax2). (Les exposants impairs donnant systématiquement des intégrales nulles par parité).
Calcul d'intégrale 2
Soit l'intégrale suivante :
on peut vérifier en utilisant la règle de Leibniz que :
DémonstrationSoit F et g définies par :
on a clairement : F(a) = g(a) = 0. Il suffit donc de montrer que leurs dérivées sont égales pour tout b > 0 pour vérifier l'identité.
On a en effet que :
en appliquant la règle de Leibniz pour F, on a :
ce qui est évidemment égal à
 .
.Intégrale de Gauss
Article détaillé : Intégrale de Gauss.L'intégrale de Gauss joue un rôle important en analyse et en calcul des probabilités, elle est définie par :
puisque la fonction est paire, on peut étendre le résultat à l'intégrale sur tout l'axe réel en doublant I. Ce résultat peut s'obtenir de plusieurs façons dont une utilisant la notion d'intégrale paramétrique.
DémonstrationL'intégrale existe puisque l'intégrand est continu et tel que, pour tout
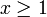 , on a :
, on a :le second membre étant évidemment intégrable sur tout l'axe réel. Considérons les deux fonctions définies par :
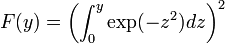 et
et ![\quad G(y) = \int_0^1{\exp[-y^2(z^2+1)]\over z^2+1}dz](/pictures/frwiki/49/17cf0eb13d015b647a771dd5046102cb.png)
elles sont toutes deux définies et continues pour tout
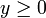 et,
et,Par ailleurs, par les propriétés de dérivabilité d'une intégrale indéfinie (F) et par la règle de Leibniz pour G, on a :
![F'(y) = 2\int_0^y\exp[-(y^2+z^2)]dz\quad](/pictures/frwiki/98/b530dea07a58675dd9bd8ab0eda36e55.png) et
et ![\quad G'(y) = -2\int_0^y y\exp[-y^2(z^2+1)]dz](/pictures/frwiki/55/7d93584b1eab9d267d0c621cdb0efb45.png)
pour y > 0 et en posant t = zy, on trouve que :
par conséquent, la fonction F + G est constante sur
![]0, +\infty[](/pictures/frwiki/101/eb8a0ceeec2805d7e3ba7c0591eafa52.png) et comme elle est continue à l'origine, on aura,
et comme elle est continue à l'origine, on aura, 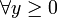 ,
,En prenant la limite à l'infini, on a :
Or cette limite vaut :
en appliquant la proposition sur l'existence d'une limite, on a :
le deuxième terme disparaissant à l'infini, on a finalement
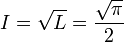 ainsi que prévu.
ainsi que prévu.Théorème de Fubini
Article détaillé : Théorème de Fubini.A l'instar de la règle de Leibniz, le théorème de Fubini tient pour l'intégrabilité d'une intégrale paramétrique dont voici une version pour le cas de l'intégrabilité au sens de Riemann.
Soit A un pavé fermé de
 , B un pavé fermé de
, B un pavé fermé de  avec
avec 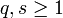 . Soit encore f une fonction bornée définie sur
. Soit encore f une fonction bornée définie sur 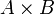 .
.Si f est intégrable au sens de Riemann sur
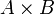 , alors,
, alors,- La fonction
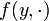 est intégrable au sens de Riemann sur B pour presque tous les y de A et l'intégrale paramétrique F1 définie par
est intégrable au sens de Riemann sur B pour presque tous les y de A et l'intégrale paramétrique F1 définie par
F1(y) = ∫ f(y,z)dz B est intégrable sur A et on a :
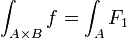 .
.- La fonction
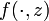 est intégrable au sens de Riemann sur A pour presque tout les z de B et l'intégrale paramétrique F2 définie par
est intégrable au sens de Riemann sur A pour presque tout les z de B et l'intégrale paramétrique F2 définie par
F2(z) = ∫ f(y,z)dy A est intégrable sur B et on a :

Si f est continue, les fonctions
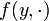 et
et 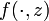 le sont aussi et le théorème de Fubini permet d'écrire :
le sont aussi et le théorème de Fubini permet d'écrire :Exemple
Soit A = [0,2], B = [1,3] et f définie sur
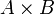 par f(x,y) = x2 + y. Elle est intégrable sur
par f(x,y) = x2 + y. Elle est intégrable sur 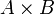 puisqu'elle est continue et on a :
puisqu'elle est continue et on a :Voir aussi
Références
- Jean MAWHIN, Analyse, fondements, techniques, évolution, 2e édition, De Boeck Université, (ISBN 978-2804124892)
- Camille DEBIEVE, Intégrales multiples, notes de cours disponible en ligne.
- Article Differentiation under the integral sign de Planet Math, lien
- Portail des mathématiques
Catégorie : Analyse
Wikimedia Foundation. 2010.

![\hat{f}(x) = \int_{\mathbb R^n}\exp[-2i\pi(x|y)]f(y)dy](/pictures/frwiki/98/bfd221c303afce07495c1fbd6af4efe9.png)
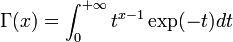
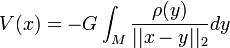
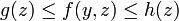
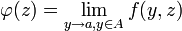
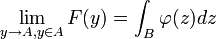
![\lim_{y\to a, y\in A} \left[\int_B f(y,z) dz\right] = \int_B\left[\lim_{y\to a, y\in A} f(y,z)\right]dz](/pictures/frwiki/50/2e8549afa05a7ce1c060718741b697e6.png)
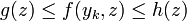

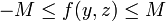
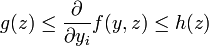

![{\partial\over\partial y_i}\left[\int_Bf(a,z)dz\right] = \int_B{\partial\over\partial y_i}f(a,z)dz](/pictures/frwiki/57/93c4612bfa2708ccdcbb9bd60487ad61.png)
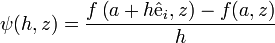
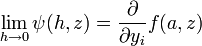
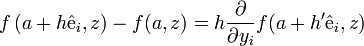

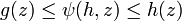

![\lim_{h\to 0} \int_B \psi(h,z) dz = \lim_{h\to 0} {1\over h}\int_B \left[f(a+h\mathrm{\hat{e}}_{i}, z) - f(a,z)\right]dz](/pictures/frwiki/52/4329bd7a4c8a92eca81986e2e5425c61.png)
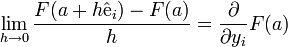
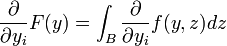
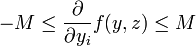
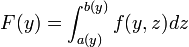
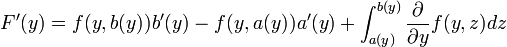
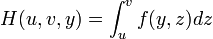
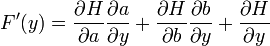
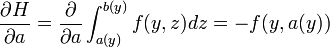
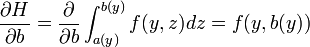
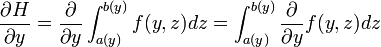
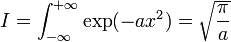
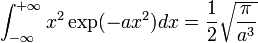
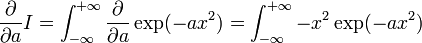
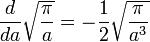
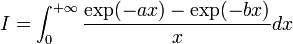



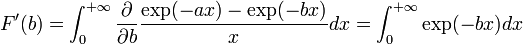
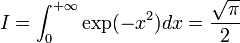
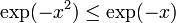

![G'(y) = -2\int_0^y\exp[-(y^2+t^2)]dt = -F'(y)](/pictures/frwiki/97/adc13b3f48189fd38bba26b7782e825b.png)
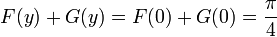
![L = \lim_{y\to \infty}[F(y)+G(y)]={\pi\over 4}](/pictures/frwiki/52/41a76b192d82caf6805c0126aeb86ce2.png)
![L = \left(\int_0^\infty \exp(-z^2)dz \right)^2 + \lim_{y\to\infty} \int_0^1{\exp[-y^2(z^2+1)]\over z^2+1}dz](/pictures/frwiki/101/ef225e3205558806f726cf0b67530c37.png)
![L = \left(\int_0^\infty \exp(-z^2)dz \right)^2 + \int_0^1\lim_{y\to\infty} {\exp[-y^2(z^2+1)]\over z^2+1}dz](/pictures/frwiki/98/b3510c91952f9183d977c6837dd0efcc.png)