Fonction inverse

Pour les articles homonymes, voir Inverse (homonymie).

Cet article traite de la fonction qui à x associe 1/x. Pour les fonctions f⁻¹ telles que si y=f(x), alors x=f⁻¹(y), voir Bijection réciproque.

En mathématiques, la fonction inverse est définie de la manière suivante :

$f:\begin{cases}\mathbb{R}^*\to\mathbb{R}^* \\x\mapsto f(x)=\displaystyle \dfrac{1}{x} \end{cases}$ .

Variations

Cette fonction est strictement décroissante sur l'ensemble des réels strictement négatifs, puis strictement décroissante sur l'ensemble des réels strictement positifs, avec 0 comme valeur interdite. On prendra garde de ne pas dire que la fonction est strictement décroissante sur $\mathbb R^*$ car si a < 0 < b, on conserve l'inégalité 1/a < 0 < 1/b

La fonction inverse n'admet pas de racine, ni de maximum ou minimum.

C'est une fonction impaire.

Dérivée de la fonction inverse

La dérivée de la fonction inverse est la fonction f' définie par:

$f':\begin{cases}\mathbb{R}^*\to\mathbb{R}^* \\x\mapsto \displaystyle f'(x)=-\dfrac{1}{x^2}\end{cases}$ .

Démonstration

Pour tout a réel non nul,

$\dfrac{f(a+h)-f(a)}{h} = \dfrac{\dfrac{1}{a+h}-\dfrac{1}{a}}{h}$

$\dfrac{f(a+h)-f(a)}{h} = \dfrac{\dfrac{a-(a+h)}{a(a+h)}}{h}$

$\dfrac{f(a+h)-f(a)}{h} = \dfrac{a-a-h}{a(a+h)}\cdot\dfrac{1}{h}$

$\dfrac{f(a+h)-f(a)}{h} = \dfrac{-1}{a(a+h)}$

Donc

$\lim_{h \to 0}\dfrac{f(a+h)-f(a)}{h} = \dfrac{-1}{a^2}$

La fonction f est donc dérivable en tout point de $\mathbb R^*$ et $f'(a) =- \dfrac{1}{a^2}$

Illustration :

Representation tangent 11 fonction inverse.png

La dérivée de $y = \dfrac{1}{x}$ au point d'abscisse 1 vaut $-\dfrac {1}{1^2} = -1$ donc la pente de la tangente à la courbe de la fonction inverse au point de coordonnées (1,1) vaut -1.

Représentation graphique

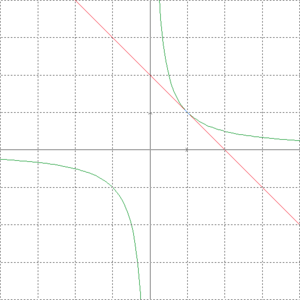
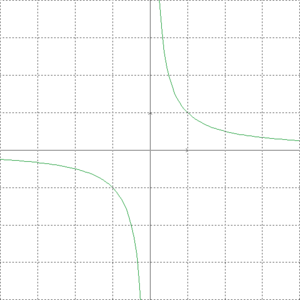
La représentation graphique de la fonction inverse est une hyperbole.

L'hyperbole d'équation $y=\frac{1}{x}$ admet deux asymptotes : une horizontale (l'axe des abscisses) et une verticale (l'axe des ordonnées). Ces deux asymptotes étant perpendiculaires, l'hyperbole est dite équilatère (son excentricité vaut $\sqrt{2}$ ).

A l'aide du graphique, il devient facile de repérer les deux types d'asymptotes présentes dans cette fonction:

une asymptote verticale, qui a pour équation : $AV : \,x=0$ ;
une asymptote horizontale, qui a pour équation : $AH :\, y=0$ .

On remarque d'autre part que cette hyperbole possède pour centre de symétrie le point O ce qui confirme le fait que la fonction inverse est une fonction impaire.

On remarque enfin que, dans un repère orthonormal, cette hyperbole possède un axe de symétrie D:y = x. En effet le point M(x ; y) appartient à (H) si et seulement si le point M'(y ; x) appartient à (H) .(y=1/x équivaut à x= 1/y). Cette propriété graphique permet de remarquer que la fonction inverse est sa propre réciproque $f \circ f = Id_{\mathbb R^*}$ . Ou bien encore, pour tout réel x non nul, l'inverse de l'inverse de x est égal à x.

Primitives de la fonction inverse

La recherche d'une primitive de la fonction inverse s'est faite tardivement. La primitive de la fonction inverse définie sur $]0 ; + \infty[$ qui s'annule en 1 s'appelle fonction logarithme népérien et est définie par: $\ln:\begin{cases}]0;+\infty[\rightarrow\mathbb{R}\\x\mapsto \ln x\end{cases}$ .

Démonstration

On considère la fonction $f(x)=e^{\ln(x)}~$

D'une part, $(e^{\ln(x)})'=(\ln x)' \cdot e^{\ln(x)} (car (e^{u})'=u' \cdot e^u~)$

donc $(e^{\ln(x)})'=(\ln x)' \cdot x~$

D'autre part, $(e^{\ln(x)})'=(x)'=1~$
Donc $1=(\ln x)' \cdot x~$

D'où $(\ln x)'=\frac{1}{x}~$

∎CQFD