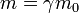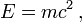- E=mc²
-
E=mc²

Cet article de physique fait
partie de la série relativitéAvant Einstein Histoire de la physique Michelson - Lorentz Mach - Poincaré - Hilbert exp:Michelson et Morley - éther Avec Einstein Principe de relativité Principe d'équivalence c - transformation de Lorentz espace-temps - E=mc² - temps exp:pensée?-jumeaux-train relativité restreinte-générale controverse historique En physique des particules cyclotron accélérateur de particules Feynman - EQR Méta Formulaire de physique Tous les articles sur la relativité L'équation E=mc2 a été formulée en 1905 par Albert Einstein dans le cadre de la relativité restreinte. Elle signifie qu'une particule isolée de masse m possède, du fait de cette masse, une énergie E, appelée énergie de masse donnée par le produit de m par le carré de la vitesse de la lumière.
Cette relation a fortement marqué les esprits car elle montre que, du fait de l'énormité du facteur c2, une masse même petite à l'échelle humaine (par exemple 1 gramme) possède une quantité considérable d'énergie (environ 1014 joules pour une masse d'un gramme). Cependant, il faut se méfier des conversions directes : d'autres lois (conservation de la charge, du nombre baryonique...) montrent qu'on ne peut espérer convertir arbitrairement la matière en énergie suivant cette formule (on peut convertir en énergie une quantité égale de matière et d'antimatière).
Sommaire
Historique
C'est avec le dernier des articles publiés lors de son annus mirabilis qu'Einstein exprime pour la première fois ce qui deviendra son équation célèbre : « Si un corps perd une énergie L sous forme de rayonnement, sa masse diminue de L/c2 »[1].
Dans ce texte, il produit une première démonstration pour le cas général de ce principe d'équivalence qui jusque-là n'avait été démontré que dans des cas particuliers[2]. Il en proposera par la suite deux autres, en 1934 et en 1946[2].
La paternité de l'équation E = mc2 a donné lieu à une controverse sur la paternité de la relativité. Par exemple, dans son livre Theory of Relativity of Poincaré and Lorentz, ainsi que dans son livre A History of the Theories of Aether and Electricity (1954), le mathématicien et historien des sciences britannique Edmund Whittaker a crédité Henri Poincaré pour l'équation E = mc2, ce qui est à son tour contesté par d'autres[3].
Illustrations
En mécanique newtonienne, l'énergie d'une particule isolée provient de sa vitesse et se manifeste sous forme d'énergie cinétique. Au contraire, d'une façon inattendue à l'époque de sa découverte, E = mc2 exprime qu'une particule de masse m possède intrinsèquement une énergie E, même si elle est au repos. Elle stipule que la masse est une forme d’énergie comme le sont l’énergie potentielle ou l’énergie cinétique. L’énergie d’un corps devient donc la somme de son énergie cinétique et de sa masse.
Cette équivalence entre masse et énergie ouvre un éventail de possibilités inconnues de la physique pré-relativiste. En relativité restreinte, la masse peut être convertie en chaleur, énergie cinétique ou autre forme d’énergie. En effet lorsque les particules d'un système donné subissent une transformation, par exemple lors d'une collision, la relativité restreinte impose que l'énergie totale (évaluée dans un certain système de coordonnées) se conserve. Mais comme l'énergie comprend la masse, il est tout-à-fait possible que de la masse apparaisse lors de la réaction (par exemple sous forme de particules) au détriment d'énergie ou que, au contraire, de l'énergie soit libérée par « consommation » de masse.
Numériquement, dans l'équation E = mc2 et dans le système international d'unités :
- E est l'énergie exprimée en joules,
- m est la masse en kilogrammes,
- c est la vitesse de la lumière dans le vide, soit 299 792 458 m/s = 2,997 924 58×108 m/s, ce qui correspond à un facteur c2 ≈ 9×1016 m2⋅s-2.
Dans le système CGS, E est en erg, m en grammes, c vaut 2,997 925×1010 cm/s et c2 ≈ 9×1020 cm2⋅s-2.
 La fameuse équation sur le pont de l'USS Enterprise lors de l'Opération Sea Orbit, dont tous les navires présents étaient propulsés grâce à l'énergie nucléaire.
La fameuse équation sur le pont de l'USS Enterprise lors de l'Opération Sea Orbit, dont tous les navires présents étaient propulsés grâce à l'énergie nucléaire.
Ce type de transformation de masse en énergie est utilisée par les piles atomiques ainsi que des bombes nucléaires. L’énergie correspondant à 1 kg de matière est énorme, car égale à 9×1016 joules : c'est l’énergie produite par un réacteur nucléaire d'une puissance de 1400 MW pendant deux ans environ. La France a produit en 2006 environ 80 % de son électricité dans des centrales nucléaires dont le bilan d'énergie peut être évalué à partir de la formule d'Einstein.
Mais cette relation n'est pas réservée au domaine du nucléaire. Par exemple en chimie, lorsque 1 kg d'hydrogène se combine avec 8 kg d'oxygène pour former de l'eau, environ 108 joules d'énergie est libérée. Cette énergie correspond à une perte de masse d'environ 10-9 kg, ce qui entraine que la masse de l'eau formée est inférieure de cette quantité à la masse initiale de 9 kilogrammes des réactifs.
Cependant le défaut de masse, de l'ordre du dixième de milliardième en valeur relative, est trop infime pour pouvoir être mis en évidence par des mesures expérimentales, qui arrivent au mieux à l'ordre du centième de millionième. C'est pour ça que l'on continue à utiliser le « théorème classique » de la conservation de la masse dans les réactions chimiques et dans la vie courante, mais en toute rigueur c'est inexact.
Néanmoins, les mesures de spectrométrie de masse les plus pointues approchent cet ordre de précision. Et alors on pourra visualiser directement l'équivalent de masse de l'énergie de liaison moléculaire, comme on le fait avec l'énergie de liaison nucléaire.
Un autre exemple illustrant l'équivalence entre masse et énergie est donné par le défaut de masse de l'atome le plus simple : la masse de l'atome d'hydrogène
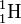 est inférieure à la somme des masses de l'électron et du proton d'une quantité juste égale à l'équivalent en masse de l'énergie d'ionisation de l'atome, bien que ce défaut soit tout à fait hors de portée de la mesure courante, puisqu'il vaut :
est inférieure à la somme des masses de l'électron et du proton d'une quantité juste égale à l'équivalent en masse de l'énergie d'ionisation de l'atome, bien que ce défaut soit tout à fait hors de portée de la mesure courante, puisqu'il vaut : 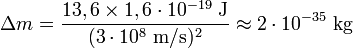 ; c'est-à-dire un dix-milliardième de la masse d'un proton...
; c'est-à-dire un dix-milliardième de la masse d'un proton...On peut encore vérifier expérimentalement que la racine carrée du rapport E/m est égale à c dans l'exemple suivant. Dans la désintégration du positronium, il y a création et émission de deux rayons gamma d'énergie (mesurée) 0,511 MeV = 0,8186×10-13 J, en compensation de la disparition de deux masses d'électron.
La masse d'un électron étant de 9,11×10-31 kg, on trouve bien :
et donc :
À l'échelle astronomique, la formule explique également comment les étoiles, comme le Soleil, peuvent émettre leur énergie pendant des dizaines de milliards d'années, alors que cette situation constituait un mystère pour la physique du début du XXe siècle, aucune source d'énergie connue à l'époque ne pouvant en rendre compte.
Au centre du Soleil, les conditions physiques sont telles que s'y produisent des réactions nucléaires capables au bout d'une chaine de processus de transformer 4 noyaux d'hydrogène (4 protons), en un noyau d'hélium. Il se trouve que la masse au repos du noyau d'hélium (4He) est inférieure à la somme des masses au repos des 2 protons et 2 neutrons qui le constituent[note 1]. L'énergie équivalente à cette différence de masse est la source de l'énergie du Soleil, et grâce à l'importance du facteur de conversion c2 et à la masse considérable du Soleil, le calcul montre que l'énergie libérée permet à notre étoile de briller pendant une bonne douzaine de milliards d'années[note 2].
Formulation générale
Si la formule E = mc2 concerne une particule au repos, c'est-à-dire une particule dont la vitesse est nulle dans le référentiel choisi, que devient cette expression dans un autre référentiel, avec une particule animée d'une vitesse v ?
Alors que la géométrie euclidienne raisonne sur des points repérés dans l'espace par trois coordonnées, la relativité restreinte raisonne sur des événements repérés dans l'espace-temps par quatre coordonnées, une de temps et trois d'espace. De même que la distance euclidienne entre deux points est invariante par changement de repère, de même la théorie relativiste stipule que le carré de l'intervalle d'espace-temps défini par :
où Δt représente l'intervalle de temps entre les deux événements et Δs la distance, est invariant par changement de repère. Autrement dit quand on mesure les coordonnées des mêmes événements dans plusieurs repères (t, x, y, z)), (t', x', y', z'), (t", x", y", z"),… différents la quantité suivante ne change pas de valeur :
Alors que la mécanique newtonienne considère d'une part l'énergie et d'autre part la quantité de mouvement d'un corps en mouvement, la relativité unifie ces deux concepts dans un objet unique : le quadrivecteur énergie-impulsion. Ce vecteur à quatre dimensions a pour composante temporelle l'énergie E/c de la particule et pour composante spatiale son vecteur impulsion (ou quantité de mouvement)
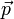 à trois dimensions. Comme il est le pendant du vecteur impulsion mv de la mécanique classique (produit de la masse par la vitesse) il est égal à m u où u est maintenant le quadrivecteur vitesse.
à trois dimensions. Comme il est le pendant du vecteur impulsion mv de la mécanique classique (produit de la masse par la vitesse) il est égal à m u où u est maintenant le quadrivecteur vitesse.De même que le carré de l'intervalle d'espace-temps était invariant par changement de coordonnées, de même l'est le carré de la norme du quadrivecteur énergie-impulsion. Autrement dit la quantité :
est indépendante du repère dans lequel on l'évalue. Mais séparément, l'énergie et l'impulsion en dépendent.
Dans le repère propre de la particule, celui où elle est au repos, la vitesse, et donc l'impulsion, est nulle. Si on note E0 l'énergie dans ce repère propre l'invariance de la quantité précédente s'écrit :
La valeur de E0 nous est donné par le fameux mc2 de sorte que l'on aboutit à l'équation capitale suivante :
ou encore :
La théorie montre que dans un repère où la vitesse de la particule est v l'énergie et la quantité de mouvement sont données par les formules :
avec la notation classique,
On vérifie que E2 − p2c2 = m2c4 et on déduit de ces formules la relation importante entre énergie et impulsion :
Cas d'une particule de masse nulle
Le cas d'une particule de masse nulle découle des formules précédentes, et notamment de :
Si une particule a une vitesse égale à c son énergie est :
Par conséquent sa masse est nulle puisqu'elle donnée par la formule :
Inversement si une particule a une masse nulle son énergie est E = pc et par conséquent v = c.
En physique des particules, plusieurs particules ont une masse nulle et se déplacent à la vitesse c, dont les photons, qui transportent le rayonnement électromagnétique, et les bosons de jauge, qui transmettent les autres interactions fondamentales du modèle standard. Le neutrino a longtemps été considéré comme une particule de masse nulle mais des expériences récentes comme celle de Super-Kamiokande font penser que cette masse serait toute petite mais pas nulle[note 3]. Dans le cadre de la relativité générale les ondes gravitationnelles se déplacent aussi à la vitesse de la lumière et la particule associée, appelée graviton, devrait être de masse nulle. Néanmoins à ce jour, et contrairement aux autres particules citées, ni le graviton ni le rayonnement gravitationnel associé n'ont été observés expérimentalement.
Unités
Énergie en unités de masse
Les formules utilisées ci-dessus sont écrites en unités conventionnelles. Mais il peut être commode d'utiliser des unités mieux adaptées à l'espace-temps, en exprimant en particulier une énergie en kilogrammes, autrement dit en prenant comme unité d'énergie l'énergie d'un kilogramme de matière.
D'après la formule :
- E(joules) = m(kilogrammes)×[c(m/s)]2,
l'énergie équivalente à la masse d'un kilogramme est :
- énergie d'un kilogramme (en joules) = [c(m/s)]2.
Par conséquent l'énergie en unités de masse sera :
- E(en unités de masse) ≡ E(en kilogrammes) = E(en joules)/(énergie d'un kilogramme en joules) ≡ E(en joules)/[c(m/s)]2
On peut donc écrire :
et en sens inverse :
Numériquement :
- 1 kg = 8,988×1016 J
- 1 J = 1,113×10-17 kg
ou dans le système CGS utilisé par habitude en astronomie :
- 1 g = 8,988×1020 erg
- 1 erg = 1,113×10-21 g
De la même façon, la réunion du temps et de l'espace en une seule entité invite le physicien à utiliser une même unité, la seconde ou le mètre, pour mesurer les longueurs et les temps[note 4].
On a les formules de passage suivantes :
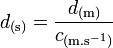
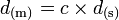 ,
,
où d(s) est le temps mis par la lumière pour parcourir d(m).
On écrit à l'identique :
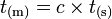 ,
,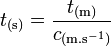
où t(m) est la distance parcourue par la lumière en t(s).
L'utilisation d'une unité commune, disons la seconde, pour mesurer distance et temps est riche d'enseignement dans le contexte présent. En effet grâce à ce choix la vitesse v, rapport d'une distance à un temps, devient sans dimension. Par conséquent l'énergie cinétique newtonienne K = (1/2)mv2 prend les dimensions d'une masse, ce qui revient à dire qu'on peut exprimer une énergie en unités de masse. On retrouve donc de façon simple, et néanmoins convenable, l'équivalence entre énergie et masse.
Ainsi, si l'énergie E est exprimée en unités de masse (par exemple en kilogrammes) la formule d'Einstein devient :
ou plus simplement :
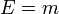 .
.
En fait, en utilisant des unités relativistes, le facteur c disparaît de toutes les formules. Ainsi la formule donnant l'invariant du vecteur énergie-impulsion s'écrit maintenant :
où Erel et prel sont exprimées en unités relativistes (c'est-à-dire en kilogrammes).
De même il est agréable d'écrire le carré du temps propre sous la forme homogène et symétrique :
sans avoir à traîner des facteurs c.
Masse en électron-volt
En sens inverse il est très courant en physique atomique de mesurer une masse en unités d'énergie. Ainsi la masse d'une particule est souvent donnée en électron-volt.
Un électron-volt vaut 1,602 176 53×10-19 joule, énergie à laquelle correspond la masse 1eV/c2, soit 1,783×10-36 kg.
On a donc les formules de passage :
Puisque le nombre sans dimensions qui mesure une certaine grandeur est par définition le rapport entre la grandeur à mesurer et la grandeur choisie pour unité, ce nombre est inversement proportionnel à la valeur de l'unité choisie (si l'unité choisie est plus grande, le nombre qui mesurera la grandeur est lui plus petit).
Ici on a donc :
- m(en eV) / m(en kg) = 1kg / 1eV,
de sorte que l'on peut écrire :
Rappelons les multiples usuels :
- 1 keV = 103 eV
- 1 MeV = 106 eV
- 1 GeV = 109 eV
- 1 TeV = 1012 eV
Par exemple, la masse de l'électron est de 511 keV, celle du proton de 938 MeV et celle du neutron est de 940 MeV.
Énergie d'une particule
L'énergie totale d'une particule isolée (qui dépend, rappelons-le, du repère choisi) peut s'écrire comme la somme de son énergie au repos mc2 et de son énergie cinétique K.
On a donc :
L'énergie cinétique devient :
- Aux faibles vitesses (c'est-à-dire petites devant celle de la lumière), on obtient :
qui n'est autre que l'énergie cinétique classique.
- Pour les vitesses très proches de celle de la lumière, l'énergie au repos de la particule s'avère négligeable devant l'énergie cinétique.
Comme on peut écrire :
l'énergie totale devient :
Autre notation
En notant m0 la masse de la particule et E0 son énergie au repos l'équation d'Einstein s'écrit :
- E0 = m0c2.
On introduit alors parfois la quantité :
qui n'est plus la vraie masse m0, mais qui, mesurant l'inertie de la particule, est parfois appelée masse inerte.
Dans ces conditions la formule écrite plus haut « E=γm0c2 » donnant l'énergie de la particule prend la même forme :
l'expression étant alors valable même dans le cas où le corps n'est pas au repos.
Cependant cet emploi est fortement déconseillé par les spécialistes. Ils font remarquer en effet que la vraie masse au repos, notée ici m0, possède une signification physique indépendante du repère choisi car son carré est l'invariant du vecteur énergie-impulsion (en unités relativistes). Or cette propriété majeure n'est pas partagée par la pseudo-masse inerte m, qui elle dépend du repère choisi et ne mérite pas le nom de masse, car elle ne correspond plus à une véritable grandeur physique. Au mieux on peut considérer la formule E = mc2 ainsi écrite comme un moyen mnémotechnique pour retenir l'expression de l'énergie mais la signification physique de cette formulation est faible.
Notes et références
- Notes
- ↑ Dans le processus de fusion nucléaire de l'hydrogène en hélium, la moitié des protons initiaux deviennent des neutrons.
- ↑ Le Soleil approche de la moitié de sa vie, lequel est âgé de quelque ~4,7 milliards d'années. Cette durée de vie (sur la séquence principale) varie d'une étoile à l'autre et dépend à la fois de la masse disponible et de l'allure à laquelle cette masse est consommée. Ce sont les étoiles massives qui ont les durées de vie les plus courtes car elles sont les plus « dépensières » relativement à leurs « réserves », même si elles sont initialement plus élevées.
- ↑ Toutefois, tant que la masse n'aura pas été mesurée, que la théorie n'aura pas de son côté éclairci la question, que la production dans le Soleil des neutrinos détectés sur Terre ne sera pas connue de façon assez sûre et que d'autres expériences n'auront pas confirmé les choses, peut-être est-il prématuré de déclarer que la question de la masse du neutrino est réglée.
- ↑ Il est courant dans la vie quotidienne d'utiliser une unité de temps pour indiquer une distance (nous disons par exemple que Montpellier est à trois heures de train de Paris).
En astronomie, il est encore plus courant de mesurer la distance d'un astre en temps de lumière par le temps qu'il faut à la lumière pour venir de l'astre en question. Ainsi dira-t-on d'une étoile qu'elle est située « à 100 années-lumière », ce qui signifie que la lumière qu'elle émet met 100 ans pour nous parvenir : celle que nous recevons aujourd'hui a été émise il y a 100 ans.
- Références
- ↑ Albert Einstein, « Ist die Trägheit eines Körpers von seinem Energiegehalt abhängig ? », Annalen der Physik, 18:639, 1905. Une traduction en langue anglaise est accessible en ligne, sous le titre Does the Inertia of a Body Depend upon its Energy-Content.
- ↑ a et b Abraham Pais, Albert Einstein. La vie et l'oeuvre, InterEditions, 1993, p. 145. ISBN 978-2729604585
- ↑ Jean Hladik, E = mc2. Histoire méconnue d'une célèbre formule, Ellipses, 2007. ISBN 2729832092
Voir aussi
Articles connexes
- Relativité restreinte
- Théorie de la relativité
- Invariance de Lorentz
- Facteur de Lorentz
- Albert Einstein
- Portail de la physique
Catégories : Équation | Physique théorique | Albert Einstein
Wikimedia Foundation. 2010.


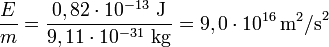
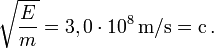
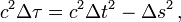
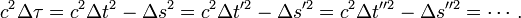
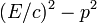
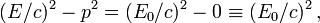
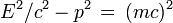
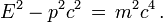
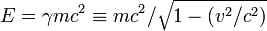
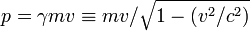
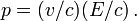
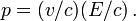
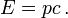
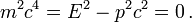
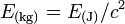
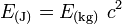
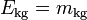
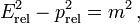
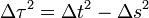

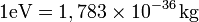
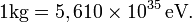
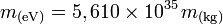
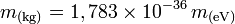
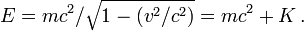
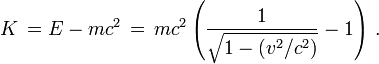
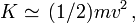
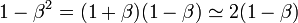
![E \simeq K = \frac{mc^2}{\sqrt{2(1-\beta)}}\equiv \frac{mc^2}{\sqrt{2[1-(v/c)]}}\,.](/pictures/frwiki/48/094a0daad581de7f363c7475e72a50b1.png)