Coordonnées généralisées

On appelle coordonnées généralisées d'un système physique un ensemble de variables réelles, qui ne correspondent pas toutes à des coordonnées cartésiennes (par exemples : angles, positions relatives), et permettant de décrire ce système, en particulier dans le cadre de la mécanique lagrangienne. Le terme « généralisées » vient de l'époque où les coordonnées cartésiennes étaient considérées comme étant les coordonnées normales ou naturelles.

Pour un système physique, on distingue les conditions physiques qui s'exercent dessus de ses contraintes, qui sont des hypothèses de rigidités, de limitations son cadre d'évolution, etc. Les contraintes du système introduisent des dépendances entre les coordonnées, et font baisser le nombre de variables numériques (coordonnées) nécessaires à sa description. Tenant compte de cela les conditions physiques déterminent l'évolution temporelle des coordonnées.

Les coordonnées généralisées ne sont pas toujours supposées indépendantes, et leur intérêt, par rapport aux seules coordonnées cartésiennes, est de pouvoir choisir les coordonnées les plus adaptées pour représenter le système, en tenant compte de ses contraintes. Par exemple, dans le cas d'un pendule, il est avantageux d'utiliser l'angle du pendule parmi les coordonnées généralisées.

Les coordonnées généralisées sont au nombre de $\ n \le 3N$ , où N est le nombre de points permettant de décrire le système et sont souvent notées

$\lbrace\mathbf{q_1},\mathbf{q_2}, ..., \mathbf{q_n} \rbrace$

L'unité de mesure des $\ q_i$ n'est pas obligatoirement une distance : par exemple des coordonnées peuvent être des angles. Il est même imaginable que chaque coordonnée ait sa propre unité de mesure.

L'objectif est d'exprimer les $\ q_i$ comme des fonctions du temps ( $\ q_i = q_i (t)$ ), un choix judicieux des $\ q_i$ aidant à approcher cet idéal. Et sachant que $\vec r = \vec r (q_1,q_2, ... , q_n, t)$ , si la description $\ q_i = q_i (t)$ est obtenue, on peut obtenir la description du système sous la forme $\vec r = \vec r (t)$ . Sauf dans les cas les plus simples, cet objectif n'est jamais atteint mais le physicien arrive en général à obtenir quand même de nombreuses informations.

Sommaire

1 Dimension et dépendance
2 Vitesse, force et accélération généralisées
3 Articles connexes
4 Bibliographie

Dimension et dépendance

Un système de N points matériels, évoluant dans l'espace physique de dimension 3, est décrit par les 3N coordonnées cartésiennes de ses points : le système peut être considéré comme un point évoluant dans un espace cartésien de dimension 3N. Les coordonnées sphériques et cylindriques sont des exemples de coordonnées généralisées sans changement du nombre de coordonnées.

Une contrainte introduit une dépendance entre ces coordonnées et on peut alors considérer que le système est un point évoluant sur une variété plongée dans l'espace cartésien de dimension 3N. Le système peut alors, en principe, être décrit par $\ n < 3N$ nombres (des « coordonnées généralisée ») et peut être considéré comme un point évoluant dans un espace de dimension n.

En général, k contraintes (équations numériques) font baisser de k le nombre de variables nécessaires à la description du système (il faut alors au moins 3N-k coordonnées généralisées), mais il peut en être autrement, suivant la nature des contraintes ou si les contraintes ne sont pas indépendantes (au moins une des équations numérique peut être obtenue à partir des autres), le nombre de variables nécessaires baisse alors de k' < k (il faut alors au moins 3N-k' coordonnées généralisées). Le nombre minimal de coordonnées généralisées (variables) nécessaires à la description du système est appelé le degré de liberté.

Pour arriver à la description $\ q_i = q_i (t)$ , choisir des coordonnées généralisées indépendantes peut être précieux (le nombre n de ces coordonnées est alors le degré de liberté du système), mais parfois il est plus facile de considérer des coordonnées dépendantes et d'utiliser les multiplicateurs de Lagrange pour tenir compte des contraintes.

Exemple de la position d'un solide dans l'espace physique

Dans l'espace, un triangle est déterminé par trois sommets (donc 9 coordonnées) soumis à trois contraintes holonomes indépendantes (les 3 contraintes de longueurs), donc il y a 9-3 = 6 degrés de liberté. Dans l'espace un triangle est donc déterminé par 6 variables indépendantes (on peut choisir les 3 coordonnées d'un des sommets et 3 angles qui permettent de déterminer les directions de deux côtés). Comme la position de tout solide rigide est déterminée par trois de ses points non-alignés quelconques, elle est déterminée par 6 variables indépendantes.

Exemple du pendule double (et plan)

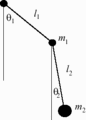
Un pendule double plan peut être décrit par les quatre coordonnées cartésiennes (dans son plan d'oscillation) de ses deux masses. Les deux contraintes holonomes que sont les longueurs de ses tiges ramènent à deux le nombre suffisant de variables pour le décrire. Un choix judicieux de variables est les deux angles $\theta_1 , \theta_2 \in [ 0 ; 2 \pi ]$ des tiges avec la verticale, chacun variant dans $\R$ , ou, par périodicité, sur un cercle $\ S_1$ : le système est équivalent à un point évoluant dans le plan $\R \times \R$ , mais du fait de la périodicité du système par rapport aux angles on peut aussi considérer qu'il évolue sur un tore $\equiv S_1 \times S_1$ ; et l'évolution temporelle des deux angles dépend des lois de la mécanique.

Deux angles déterminent le pendule double
Les deux angles correspondent à un point évoluant sur un tore

Vitesse, force et accélération généralisées

La vitesse généralisée est définie dans la droite ligne des coordonnées généralisées, par contre la force et l'accélération généralisées sont définies à l'aide des déplacements virtuels dans le but de s'incérer dans la mécanique analytique qui les utilise intensément.

Vitesse généralisée

Pour un point de l'espace physique (de dimension trois), la vitesse est définie à partir du vecteur $\vec r (t)$ des coordonnées cartésiennes comme étant égale à Erreur math (La conversion en PNG a échoué ; vérifiez l’installation de latex et dvipng (ou dvips + gs + convert)): \vec v = \dot \vec r = \frac{d \vec r}{dt} .

Avec des coordonnées généralisées $\ \lbrace {q_1},{q_2}, ...,{q_n} \rbrace$ , la vitesse généralisée est le vecteur de dimension n : $\ \lbrace {\dot q_1},{\dot q_2}, ...,{\dot q_n} \rbrace$ où $\ \dot q_i = \frac{d q_i}{dt}$ .

On peut remarquer que si les trois coordonnées de la vitesse Erreur math (La conversion en PNG a échoué ; vérifiez l’installation de latex et dvipng (ou dvips + gs + convert)): \vec v = \dot \vec r

sont en unité longueur.temps^-1, il n'en est plus obligatoirement de même avec la vitesse généralisée du fait que les  ne sont pas obligatoirement en unité de longueur.

Force généralisée

Dans l'espace physique à trois dimensions, une force $\ \vec F_i$ s'exerçant sur les points i du système, le travail de cette force au cours d'un déplacement virtuel $\delta \vec r_i$ est $\delta W = \sum_i \vec F_i . \delta \vec r_i$ . Du fait que les déplacements considérés sont virtuels, on parle de travail virtuel de la force.

Avec n coordonnées généralisées $\ \lbrace {q_1},{q_2}, ...,{q_n} \rbrace$ , on a $\ \delta \vec r = \sum_{j=1}^n \frac{\partial \vec r}{\partial q_j} . \delta q_j$ et la volonté est de définir une force $\ Q = \left( {Q_1},{Q_2}, ...,{Q_n} \right)$ de dimension n qui corresponde à la force $\ \vec F_i$ de telle sorte que $\ \delta W = \sum_i \vec F_i . \delta \vec r_i = \sum_{j=1}^n Q_j . \delta q_j$ .

La définition correspondante est : $\ Q_j = \sum_i \vec F_i . \frac{\partial \vec r_i}{\partial q_j}$ , pour chaque coordonnée n° $\ j \in \{ 1; 2; ... ; n\}$ .

Il faut prendre garde au fait qu'il ne peut s'agir que d'une définition car l'égalité $\ \sum_i \vec F_i . \delta \vec r_i = \sum_{j=1}^n Q_j . \delta q_j$ ne permet de justifier $\ Q_j = \sum_i \vec F_i . \frac{\partial \vec r_i}{\partial q_j}$ que dans le cas où les n déplacements virtuels $\ {\delta q_1},{\delta q_2}, ...,{\delta q_n}$ sont indépendants : on peut alors les choisir tous nuls sauf un et ainsi établir l'égalité voulue. Dans le cas où les n coordonnées généralisées ne sont pas indépendantes, elles sont soumises à des contraintes, et les déplacements virtuels associés sont définis comme devant respecter ces contraintes : les $\ \delta q_j$ ne peuvent pas être choisis indépendamment les uns des autres et il y a d'autres choix possibles pour $\ Q_j$ .

De même que pour la vitesse généralisée, les unités de mesure des n coordonnées de l'accélération généralisée ne sont pas obligatoirement le newton.

Accélération généralisée

L'accélération généralisée se définit de manière similaire à la force généralisée, en y faisant intervenir les masses des corps ponctuels, afin d'utiliser la force $\ m_i .\vec a_i$ qui s'exerce sur le système et ensuite de travailler en respectant le principe fondamental de la dynamique : si $\ \vec a_i$ est une accélération subie par chaque point i de masse $\ m_i$ du système dans l'espace physique à trois dimensions, l'accélération généralisée correspondante est le vecteur de dimension n $\ A = \left( A_1 ; A_2; ... ; A_n \right)$ défini par $\ A_j = \sum_i m_i .\vec a_i . \frac{\partial \vec r_i}{\partial q_j}$ , pour chaque coordonnée n° $\ j \in \{ 1; 2; ... ; n\}$ .

L'unité de mesure de chaque coordonnée de l'accélération généralisée est la même que la coordonnée correspondante d'une force généralisée.

Bibliographie

Claude Gignoux et Bernard Silvestre-Brac ; Mécanique : de la formulation lagrangienne au chaos hamiltonien, éditeur EDP-Sciences, 2002, 467 pages ISBN 2868835848.

Portail de la physique

Catégories :

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Coordonnées généralisées de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Coordonnees generalisees — Coordonnées généralisées On appelle coordonnées généralisées d un système physique un ensemble de variables réelles indépendantes permettant de décrire ce système, en particulier dans le cadre de la mécanique lagrangienne. Leur nom provient de l… … Wikipédia en Français
Coordonnées Généralisées — On appelle coordonnées généralisées d un système physique un ensemble de variables réelles indépendantes permettant de décrire ce système, en particulier dans le cadre de la mécanique lagrangienne. Leur nom provient de l époque où les coordonnées … Wikipédia en Français
coordonnées généralisées — apibendrintosios koordinatės statusas T sritis fizika atitikmenys: angl. generalized coordinates vok. verallgemeinerte Koordinaten, f rus. обобщённые координаты, f pranc. coordonnées généralisées, f … Fizikos terminų žodynas
Coordonnées plückeriennes — Les Coordonnées plückeriennes sont un cas particuliers des coordonnées grassmanniennes. Elles servent à repérer les plans d un espace de dimension 4. Réalisées par Julius Plücker, elles ont été généralisées entre 1832 et 1839 par Hermann… … Wikipédia en Français
Systeme de coordonnees — Système de coordonnées Pour les articles homonymes, voir Système de coordonnées (homonymie). En mathématiques, un système de coordonnées permet de faire correspondre à chaque point d un espace à N dimensions, un N uplet de scalaires. Dans… … Wikipédia en Français
Système de coordonnées — Pour les articles homonymes, voir Système de coordonnées (homonymie). En mathématiques, un système de coordonnées permet de faire correspondre à chaque point d un espace à N dimensions, un N uplet de scalaires. Dans beaucoup de cas, les scalaires … Wikipédia en Français
Mecanique hamiltonienne — Mécanique hamiltonienne Pour les articles homonymes, voir Hamilton. La mécanique hamiltonienne, inventée par Hamilton en 1833, est une reformulation de la mécanique classique. Son formalisme a facilité l élaboration théorique de la mécanique… … Wikipédia en Français
Mécanique Hamiltonienne — Pour les articles homonymes, voir Hamilton. La mécanique hamiltonienne, inventée par Hamilton en 1833, est une reformulation de la mécanique classique. Son formalisme a facilité l élaboration théorique de la mécanique quantique. Sommaire 1… … Wikipédia en Français
Mécanique de Hamilton — Mécanique hamiltonienne Pour les articles homonymes, voir Hamilton. La mécanique hamiltonienne, inventée par Hamilton en 1833, est une reformulation de la mécanique classique. Son formalisme a facilité l élaboration théorique de la mécanique… … Wikipédia en Français
Mécanique hamiltonienne — Pour les articles homonymes, voir Hamilton. La mécanique hamiltonienne, inventée par Hamilton en 1833, est une reformulation de la mécanique classique. Son formalisme a facilité l élaboration théorique de la mécanique quantique. Sommaire 1… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Coordonnées généralisées

Sommaire

Dimension et dépendance