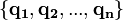Coordonnées Généralisées

Coordonnées Généralisées

Coordonnées généralisées

On appelle coordonnées généralisées d'un système physique un ensemble de variables réelles indépendantes permettant de décrire ce système, en particulier dans le cadre de la mécanique lagrangienne. Leur nom provient de l'époque où les coordonnées cartésiennes étaient considérées comme étant les coordonnées normales ou naturelles.

Un système possédant n degrés de liberté peut être entièrement décrit à l'aide de n coordonnées généralisées indépendantes, généralement notées

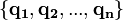
\lbrace\mathbf{q_1},\mathbf{q_2}, ..., \mathbf{q_n} \rbrace

L'intérêt des coordonnées généralisées par rapport aux seules coordonnées cartésiennes est de pouvoir choisir les coordonnées les plus adaptées pour représenter le système. Par exemple, dans le cas d'un pendule, il s'agit de l'angle et de la vitesse du pendule.

Voir aussi

Contrainte holonome

  • Portail de la physique Portail de la physique
Ce document provient de « Coordonn%C3%A9es g%C3%A9n%C3%A9ralis%C3%A9es ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Coordonnées Généralisées de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Coordonnees generalisees — Coordonnées généralisées On appelle coordonnées généralisées d un système physique un ensemble de variables réelles indépendantes permettant de décrire ce système, en particulier dans le cadre de la mécanique lagrangienne. Leur nom provient de l… …   Wikipédia en Français

  • Coordonnées généralisées — On appelle coordonnées généralisées d un système physique un ensemble de variables réelles, qui ne correspondent pas toutes à des coordonnées cartésiennes (par exemples : angles, positions relatives), et permettant de décrire ce système, en… …   Wikipédia en Français

  • coordonnées généralisées — apibendrintosios koordinatės statusas T sritis fizika atitikmenys: angl. generalized coordinates vok. verallgemeinerte Koordinaten, f rus. обобщённые координаты, f pranc. coordonnées généralisées, f …   Fizikos terminų žodynas

  • Coordonnées plückeriennes — Les Coordonnées plückeriennes sont un cas particuliers des coordonnées grassmanniennes. Elles servent à repérer les plans d un espace de dimension 4. Réalisées par Julius Plücker, elles ont été généralisées entre 1832 et 1839 par Hermann… …   Wikipédia en Français

  • Systeme de coordonnees — Système de coordonnées Pour les articles homonymes, voir Système de coordonnées (homonymie). En mathématiques, un système de coordonnées permet de faire correspondre à chaque point d un espace à N dimensions, un N uplet de scalaires. Dans… …   Wikipédia en Français

  • Système de coordonnées — Pour les articles homonymes, voir Système de coordonnées (homonymie). En mathématiques, un système de coordonnées permet de faire correspondre à chaque point d un espace à N dimensions, un N uplet de scalaires. Dans beaucoup de cas, les scalaires …   Wikipédia en Français

  • Mecanique hamiltonienne — Mécanique hamiltonienne Pour les articles homonymes, voir Hamilton. La mécanique hamiltonienne, inventée par Hamilton en 1833, est une reformulation de la mécanique classique. Son formalisme a facilité l élaboration théorique de la mécanique… …   Wikipédia en Français

  • Mécanique Hamiltonienne — Pour les articles homonymes, voir Hamilton. La mécanique hamiltonienne, inventée par Hamilton en 1833, est une reformulation de la mécanique classique. Son formalisme a facilité l élaboration théorique de la mécanique quantique. Sommaire 1… …   Wikipédia en Français

  • Mécanique de Hamilton — Mécanique hamiltonienne Pour les articles homonymes, voir Hamilton. La mécanique hamiltonienne, inventée par Hamilton en 1833, est une reformulation de la mécanique classique. Son formalisme a facilité l élaboration théorique de la mécanique… …   Wikipédia en Français

  • Mécanique hamiltonienne — Pour les articles homonymes, voir Hamilton. La mécanique hamiltonienne, inventée par Hamilton en 1833, est une reformulation de la mécanique classique. Son formalisme a facilité l élaboration théorique de la mécanique quantique. Sommaire 1… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”