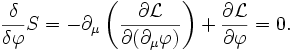- Mécanique lagrangienne
-
Lagrangien
Le lagrangien
![\mathcal{L}[\varphi_i]](/pictures/frwiki/98/b9c3f5e4b34fb0ba13145ec0678fb4d3.png) d'un système dynamique est une fonction des variables dynamiques qui permet d'écrire de manière concise les équations du mouvement du système. Son nom vient de Joseph Louis Lagrange, qui a établi les principes du procédé. Attention, malgré l'emploi du même mot, le seul rapport avec le lagrangien que l'on trouve en optimisation est que lorsque l'on ajoute des contraintes géométriques ou cinématiques le critère gagne des termes avec multiplicateurs de Lagrange, cependant lorsque toutes les forces sont conservatives et introduites par un potentiel il n'y a aucun multiplicateur et ce n'est pas un 'lagrangien' au sens mathématique du terme.
d'un système dynamique est une fonction des variables dynamiques qui permet d'écrire de manière concise les équations du mouvement du système. Son nom vient de Joseph Louis Lagrange, qui a établi les principes du procédé. Attention, malgré l'emploi du même mot, le seul rapport avec le lagrangien que l'on trouve en optimisation est que lorsque l'on ajoute des contraintes géométriques ou cinématiques le critère gagne des termes avec multiplicateurs de Lagrange, cependant lorsque toutes les forces sont conservatives et introduites par un potentiel il n'y a aucun multiplicateur et ce n'est pas un 'lagrangien' au sens mathématique du terme.Les équations du mouvement s'obtiennent par application du principe de moindre action (ou principe d'action extrémale), qui s'écrit :
avec l'action
![\mathcal{S}[\varphi_i] = \int{\mathcal{L}[\varphi_i(s)]{}\,d^ns},](/pictures/frwiki/54/6d1ddad9e9382dec25e2d70071bb51e5.png)
et
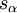 l'ensemble des paramètres du système.
l'ensemble des paramètres du système.Les équations du mouvement obtenues sont équivalentes aux équations d'Euler-Lagrange. Un système dynamique dont les équations du mouvement peuvent s'obtenir à partir d'un principe de moindre action et d'un lagrangien est un système dynamique lagrangien. C'est le cas de la version classique du modèle standard, des équations de Newton, des équations de la relativité générale, et de problèmes purement mathématiques comme les équations des géodésiques ou le problème de Plateau.
Sommaire
Un exemple en mécanique classique
Le concept de lagrangien fut historiquement introduit dans une reformulation de la mécanique classique, la mécanique lagrangienne. Dans ce contexte, le lagrangien vaut généralement l'énergie cinétique à laquelle on soustrait l'énergie potentielle :
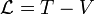
En coordonnées cartésiennes
Le lagrangien d'une particule de masse m non relativiste dans un espace euclidien à trois dimensions s'écrit :
ou bien
avec P la quantité de mouvement
on note la dérivation temporelle par un point au dessus de la quantité différentiée. Les équations d'Euler-Lagrange s'écrivent :
L'indice i = 1, 2, 3. Le calcul des dérivées donne :
P=m.v
Les équations d'Euler-Lagrange s'écrivent donc explicitement :
soit sous forme vectorielle :
Les approches lagrangienne et newtonienne sont donc équivalentes lorsque la force dérive d'un potentiel :
puisque la formulation de la deuxième loi de Newton dans un référentiel Galiléen s'écrit :
En coordonnées sphériques
Soit un espace à trois dimensions en coordonnées sphériques
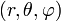 , et le lagrangien :
, et le lagrangien :Les équations d'Euler-Lagrange s'écrivent alors :
Ici l'ensemble des paramètres
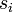 se réduit au temps
se réduit au temps 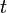 , et les variables dynamiques
, et les variables dynamiques 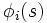 sont les trajectoires
sont les trajectoires 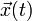 des particules.
des particules.Lagrangiens et densités de lagrangien dans la théorie des champs
Dans la théorie des champs, on distingue parfois le lagrangien L, dont l'intégrale sur le temps est l'action :
et la densité lagrangienne
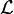 , qu'on intègre sur tout l'espace pour obtenir l'action :
, qu'on intègre sur tout l'espace pour obtenir l'action :Le lagrangien est ainsi l'intégrale spatiale de la densité lagrangienne. Cependant, on appelle souvent
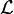 simplement le lagrangien, surtout dans l'usage moderne. C'est plus simple dans les théories relativistes où l'espace est défini localement. Ces deux types de lagrangiens peuvent être vus comme des cas particuliers d'une formule plus générale, selon qu'on introduit la variable spatiale
simplement le lagrangien, surtout dans l'usage moderne. C'est plus simple dans les théories relativistes où l'espace est défini localement. Ces deux types de lagrangiens peuvent être vus comme des cas particuliers d'une formule plus générale, selon qu'on introduit la variable spatiale 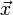 dans les index i ou dans les paramètres s pour écrire
dans les index i ou dans les paramètres s pour écrire 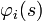 . Les théories quantiques des champs en physique des particules, comme l'électrodynamique quantique, sont généralement écrites en termes de densités de lagrangiens
. Les théories quantiques des champs en physique des particules, comme l'électrodynamique quantique, sont généralement écrites en termes de densités de lagrangiens 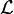 , ces termes se transformant facilement pour donner les règles permettant d'évaluer les diagrammes de Feynman.
, ces termes se transformant facilement pour donner les règles permettant d'évaluer les diagrammes de Feynman.Lagrangien électromagnétique
En général, en mécanique lagrangienne, le lagrangien vaut:
- L = T − V
où T est l'énergie cinétique et V l'énergie potentielle.
Etant donnée une particule chargée électriquement de masse m et charge q, et de vitesse
 dans un champ électromagnétique de potentiel scalaire φ et de potentiel vecteur
dans un champ électromagnétique de potentiel scalaire φ et de potentiel vecteur 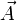 , l'énergie cinétique de la particule est :
, l'énergie cinétique de la particule est :et son énergie potentielle est:
Le lagrangien électromagnétique est alors:
DémonstrationLe lagrangien électromagnétique se construit à partir de l'expression de la force de Lorentz :
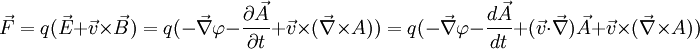
Les deux termes du membre de droite est un gradient d'un produit scalaire, la force est le gradient de l'énergie cinétique (par rapport à la vitesse) dérivée par rapport au temps obtenant :
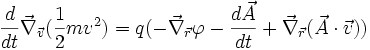
Le reste n'est plus qu'une question d'écriture :
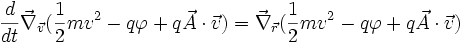
Lagrangiens en théorie quantique des champs
Le lagrangien de Dirac
La densité lagrangienne pour un champ de Dirac est:
où ψ est un spineur,
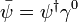 est son adjoint de Dirac, D est la dérivée covariante de jauge, et
est son adjoint de Dirac, D est la dérivée covariante de jauge, et 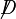 est la notation de Feynman pour γσDσ.
est la notation de Feynman pour γσDσ.Le lagrangien de l'électrodynamique quantique
La densité lagrangienne en QED est:
où Fμν est le tenseur électromagnétique.
Le lagrangien de la chromodynamique quantique
La densité lagrangienne en QCD est [1] [2] [3]
où D est la dérivée covariante de jauge en QCD, et Gαμν est le tenseur de la force du champ du gluon.
Formalisme mathématique
Soit M une variété de dimension n, et une variété de destination T. Soit
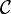 l'espace de configuration de la fonction continue s de M dans T.
l'espace de configuration de la fonction continue s de M dans T.Avant tout donnons quelques exemples :
- En mécanique classique, dans le formalisme d'Hamilton, M est le variété de dimension 1
 , qui représente le temps, et l'espace de destination est le fibré cotangent de l'espace des positions généralisées.
, qui représente le temps, et l'espace de destination est le fibré cotangent de l'espace des positions généralisées. - Dans la théorie des champs, M est la variété espace-temps et l'espace de destination est l'ensemble des valeurs possibles des champs en chaque point. Si par exemple il y a m champs scalaires réels φ1,...,φm, alors la variété de destination est
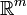 . Si on a un champ de vecteurs réels, la variété de destination est isomorphe à
. Si on a un champ de vecteurs réels, la variété de destination est isomorphe à  . Il y a en fait une manière plus élégante d'utiliser le fibré tangent, mais on s'en tiendra à cette version.
. Il y a en fait une manière plus élégante d'utiliser le fibré tangent, mais on s'en tiendra à cette version.
Supposons maintenant qu'il existe une fonctionnelle
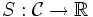 , qu'on appelle l'action physique. C'est une application vers
, qu'on appelle l'action physique. C'est une application vers  , et non vers
, et non vers  , pour des raisons physiques.
, pour des raisons physiques.Pour que l'action soit locale, nous avons besoin de restrictions supplémentaires sur l'action. Si
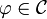 , on impose que S[φ] soit l'intégrale sur M d'une fonction de φ, de ses dérivées et des positions qu'on appelle le lagrangien
, on impose que S[φ] soit l'intégrale sur M d'une fonction de φ, de ses dérivées et des positions qu'on appelle le lagrangien 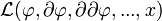 . En d'autres termes,
. En d'autres termes,La plupart du temps, on impose que le lagrangien dépende uniquement de la valeur des champs, de leur dérivées premières, mais pas des dérivées d'ordre supérieur. C'est en fait seulement par commodité, et ce n'est pas vrai en général. Nous le supposons cependant dans le reste de cet article.
Fixons des conditions aux limites, essentiellement la donnée de φ aux frontières si M est compact, ou une limite pour φ quand x tend vers l'infini (ce qui est être pratique lors d'intégrations par parties). Le sous-espace de
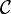 des fonctions φ telles que toutes les dérivées fonctionnelles de l'action S en φ soient 0 et que φ satisfasse aux conditions aux limites, est l'espace des solutions physiques.
des fonctions φ telles que toutes les dérivées fonctionnelles de l'action S en φ soient 0 et que φ satisfasse aux conditions aux limites, est l'espace des solutions physiques.La solution est donnée par les équations d'Euler-Lagrange (en utilisant les conditions aux limites) :
On retrouve la dérivée fonctionnnelle par rapport à φ de l'action dans le membre de gauche.
Voir aussi
- mécanique hamiltonienne
- théorème de Noether
- dérivée fonctionnelle
- intégrale de chemin (ou intégrale fonctionnelle)
- action (physique)
- principe de moindre action
- condition de cohérence
- Portail de la physique
Catégories : Physique théorique | Analyse à plusieurs variables | Géométrie différentielle | Mécanique | Géométrie symplectique
Wikimedia Foundation. 2010.

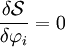
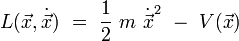
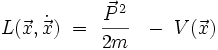
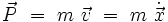
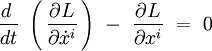
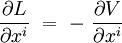
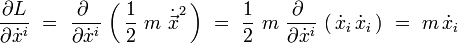
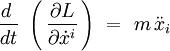
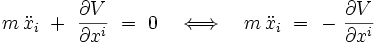
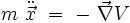
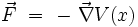
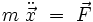
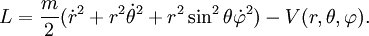
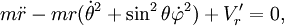
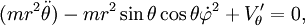
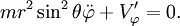
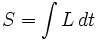
![S [\varphi_i] = \int{\mathcal{L} [\varphi_i (x)]\, d^4x}](/pictures/frwiki/101/e4f526bbf4b6bda0d1d694eadd7675c9.png)
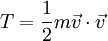
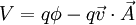
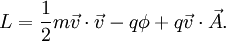
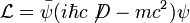
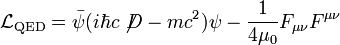
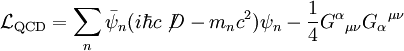
![\forall\varphi\in\mathcal{C}\, S[\varphi]\equiv\int_M d^nx \mathcal{L}(\varphi(x),\partial\varphi(x),\partial\partial\varphi(x), ...,x).](/pictures/frwiki/56/8842702deb6e823fd032233b7638c950.png)