- Coefficient binômial
-
Coefficient binomial
En mathématiques, (algèbre et dénombrement) les coefficients binomiaux , définis pour tout entier naturel n et tout entier naturel k inférieur ou égal à n, donnent le nombre de sous-ensembles différents à k éléments que l'on peut former à partir d'un ensemble contenant n éléments. On les note
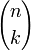 (lu « k parmi n » ) ou
(lu « k parmi n » ) ou 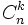 (lu « combinaison de k parmi n »). Cette quantité s'exprime à l'aide de la fonction factorielle :
(lu « combinaison de k parmi n »). Cette quantité s'exprime à l'aide de la fonction factorielle :
Les coefficients binomiaux interviennent dans de nombreux domaines des mathématiques : développement du binôme, dénombrement, développement en série, lois de probabilités.On peut les généraliser, sous certaines conditions, aux nombres complexes.
Sommaire
Établissement de la formule
L'expression de
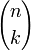 se détermine en utilisant les arrangements. On calcule le nombre d'arrangements ou de listes ordonnées à k éléments pris dans un ensemble en contenant n de deux façons différentes. La confrontation des deux calculs donne l'expression algébrique de
se détermine en utilisant les arrangements. On calcule le nombre d'arrangements ou de listes ordonnées à k éléments pris dans un ensemble en contenant n de deux façons différentes. La confrontation des deux calculs donne l'expression algébrique de 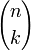
- Une liste ordonnée de k éléments pris parmi n peut être constituée en choisissant le premier élément parmi n, (n choix possibles), puis le deuxième élément parmi n -1 (n -1 choix possibles) , etc. le dernier élément étant choisi parmi n - k+1 éléments. Il existe donc
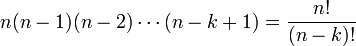 listes ordonnées de k éléments pris parmi n.
listes ordonnées de k éléments pris parmi n. - Mais on peut aussi choisir d'abord le sous-ensemble des k éléments parmi n (
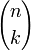 choix possibles) puis ordonner l'ensemble pour constituer une liste (k! ordres possibles). Il existe donc
choix possibles) puis ordonner l'ensemble pour constituer une liste (k! ordres possibles). Il existe donc 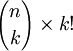 listes ordonnées de k éléments pris parmi n.
listes ordonnées de k éléments pris parmi n.
En confrontant ces deux expressions, on obtient l'expression de
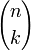 :
:Définition algébrique des coefficients binomiaux d'entiers
Le coefficient binomial des entiers naturels n et k est noté
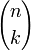 ou
ou 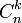 et vaut :
et vaut :Ici n ! désigne la factorielle de n. On remarque qu'il existe deux notations : le coefficient binomial de n et k s'écrit
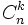 ou
ou 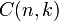 et se lit « combinaison de k parmi n » ou aussi « cnk »,
et se lit « combinaison de k parmi n » ou aussi « cnk »,- ou bien
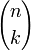 et se lit « k parmi n ».
et se lit « k parmi n ».
Une importante relation, la formule de Pascal, lie les coefficients binomiaux :
Elle donne lieu au triangle de Pascal qui permet un calcul rapide des coefficients pour de petites valeurs de n :
ligne 0 1 ligne 1 1 1 ligne 2 1 2 1 ligne 3 1 3 3 1 ligne 4 1 4 6 4 1 ligne 5 1 5 10 10 5 1 ligne 6 1 6 15 20 15 6 1 ligne 7 1 7 21 35 35 21 7 1
Les coefficients
![{n \choose k}, k \in [\![0;n]\!]](/pictures/frwiki/54/6b6fa634462895b18a40e13cc32c5e49.png) figurent à la ne ligne. Le triangle est construit en plaçant des 1 aux extrémités de chaque ligne et en complétant la ligne en reportant la somme des deux nombres adjacents de la ligne supérieure. Cette méthode permet le calcul rapide des coefficients binomiaux sans division ni multiplication.
figurent à la ne ligne. Le triangle est construit en plaçant des 1 aux extrémités de chaque ligne et en complétant la ligne en reportant la somme des deux nombres adjacents de la ligne supérieure. Cette méthode permet le calcul rapide des coefficients binomiaux sans division ni multiplication.Note : pour
![k \in [\![0;n]\!]](/pictures/frwiki/98/bd87c214fbdff923c48a39b23da46abc.png) , le coefficient binomial est un nombre entier.Démonstration
, le coefficient binomial est un nombre entier.DémonstrationLa preuve de cette propriété se fait par induction :
- Pour
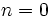 , c'est évident.
, c'est évident. - Supposons que c'est vrai pour
 .
. - Regardons ce qui se passe lorsque
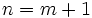 :
:
- pour
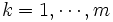 , la formule de Pascal
, la formule de Pascal 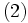 donne
donne 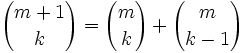
on y voit que
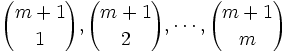 sont des entiers étant chacun la somme de deux entiers,
sont des entiers étant chacun la somme de deux entiers,alors que
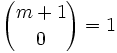 et
et 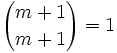 .
.- La propriété est donc vraie pour
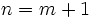 , elle est par conséquent vraie pour tout
, elle est par conséquent vraie pour tout 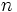 .
.
Utilisation des coefficients binomiaux
Développement du binôme de Newton
Article détaillé : Formule du binôme de Newton.Ces nombres sont les coefficients qui apparaissent en développant la puissance nieme de x + y :
Par exemple, en regardant la cinquième ligne du triangle de Pascal, on obtient immédiatement que :
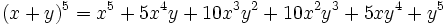 .
.
Combinatoire et statistique
Article détaillé : Loi binomiale.Les coefficients binomiaux sont importants en combinatoire, parce qu'ils fournissent des formules utilisées dans des problèmes fréquents de dénombrement :
- Le nombre de parties à k éléments dans un ensemble à n éléments est égal à
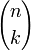 . C'est également le nombre de listes de longueur n, constituées de 1 et de 0, et ayant k fois l'élément 1 et n-k l'élément 0. Ces parties ou ces listes sont appelées des k-combinaisons sans répétition.
. C'est également le nombre de listes de longueur n, constituées de 1 et de 0, et ayant k fois l'élément 1 et n-k l'élément 0. Ces parties ou ces listes sont appelées des k-combinaisons sans répétition. - Le nombre de suites de n entiers naturels dont la somme vaut k est égale à
 . C'est aussi le nombre de façons de choisir k éléments d'un ensemble à n éléments si les répétitions sont permises (nombre de combinaisons avec répétition).
. C'est aussi le nombre de façons de choisir k éléments d'un ensemble à n éléments si les répétitions sont permises (nombre de combinaisons avec répétition). - En probabilité et statistique, les coefficients de binôme apparaissent dans la définition de la loi binomiale .
- Ils interviennent dans la définition des polynômes de Bernstein et dans l'équation paramétrique d'une courbe de Bézier.
- D'un point de vue plus intuitif, ce nombre permet de savoir combien de tirages de k éléments parmi n différents on peut réaliser. Exemple: les quatre as d'un jeu de cartes sont face contre table, on veut savoir combien de possibilités de jeu il existe si l'on prend simultanément deux cartes au hasard. Si l'on suit la formule il y en a six.
-
- Pour s'en persuader, voici la liste des mains :
- as de cœur et as de carreau
- as de cœur et as de trèfle
- as de cœur et as de pique
- as de carreau et as de trèfle
- as de carreau et as de pique
- as de trèfle et as de pique
- Il n'existe pas d'autres possibilités vu que l'ordre n'importe pas (« carreau - pique » est équivalent à « pique - carreau »).
Diviseurs et coefficients binomiaux
Les diviseurs premiers de
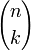 possèdent la propriété suivante : Si
possèdent la propriété suivante : Si 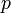 est un nombre premier et
est un nombre premier et 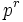 est la plus grande puissance de
est la plus grande puissance de 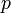 qui divise
qui divise 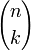 , alors
, alors 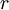 est égal au nombre d'entiers naturels
est égal au nombre d'entiers naturels 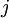 tels que la partie fractionnaire de
tels que la partie fractionnaire de  soit plus grande que la partie fractionnaire de
soit plus grande que la partie fractionnaire de  . C'est le nombre de retenues dans la soustraction de n par k, lorsque ces deux nombres sont écrits en base p.
. C'est le nombre de retenues dans la soustraction de n par k, lorsque ces deux nombres sont écrits en base p.En particulier,
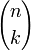 est toujours divisible par
est toujours divisible par 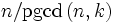 (pgcd signifie plus grand commun diviseur).
(pgcd signifie plus grand commun diviseur).
La règle permet de déterminer les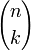 qui sont pairs. Il suffit pour cela de prendre p = 2 et
qui sont pairs. Il suffit pour cela de prendre p = 2 et  . La soustraction de n par k nécessite donc au moins une retenue en binaire. Cela signifie que, dans le développement binaire de n, il se trouve au moins un 0 situé au même rang qu'un 1 dans le développement binaire de k.
. La soustraction de n par k nécessite donc au moins une retenue en binaire. Cela signifie que, dans le développement binaire de n, il se trouve au moins un 0 situé au même rang qu'un 1 dans le développement binaire de k.A l'inverse,
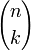 est impair si, à chaque fois que k possède un 1 dans son développement binaire, il en est de même de n au même rang. On dit que k implique n. Par exemple, si n est de la forme 2p − 1, tous ses chiffres binaires valent 1, et tous les
est impair si, à chaque fois que k possède un 1 dans son développement binaire, il en est de même de n au même rang. On dit que k implique n. Par exemple, si n est de la forme 2p − 1, tous ses chiffres binaires valent 1, et tous les 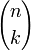 seront impairs. Si n = 2p, alors n possède un seul 1 dans son développement binaire, et seuls
seront impairs. Si n = 2p, alors n possède un seul 1 dans son développement binaire, et seuls 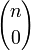 et
et  sont impairs, tous les autres sont pairs.
sont impairs, tous les autres sont pairs.Généralisations
L'écriture de
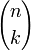 , pour tout entier n et tout entier k compris entre 1 et n, sous la forme
, pour tout entier n et tout entier k compris entre 1 et n, sous la formepermet d'envisager une extension possible aussi pour tout entier n négatif et tout entier k strictement positif en utilisant l'expression suivante :
Si l'on pose n=-m, on a la relation suivante :
C'est cette forme des coefficients binomiaux qui est utilisée dans la formule du binôme négatif ainsi que dans la définition de la loi binomiale négative
Pour tout nombre complexe z et tout entier naturel k, on définit le coefficient binomial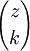 de la manière suivante :
de la manière suivante :C'est cette forme des coefficients binomiaux qui est utilisée dans la formule du binôme généralisée.
Pour tout entier k, l'expression
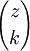 est un polynôme en z de degré k à coefficients rationnels. Tout polynôme p(z) de degré d peut être écrit sous la forme
est un polynôme en z de degré k à coefficients rationnels. Tout polynôme p(z) de degré d peut être écrit sous la formeLe calcul de
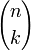 peut se généraliser, à l'aide de la fonction Gamma. On remarque que, pour tout entier naturel n, n! = Γ(n + 1), ainsi, l'on a, pour tout entier n et pour tout entier k inférieur ou égal à n,
peut se généraliser, à l'aide de la fonction Gamma. On remarque que, pour tout entier naturel n, n! = Γ(n + 1), ainsi, l'on a, pour tout entier n et pour tout entier k inférieur ou égal à n,Comme la fonctionΓ est définie pour tout complexe de
 , on peut généraliser le coefficient binomial à tous complexes s et t différents des entiers négatifs et tels que s - t ne soit pas un entier négatif, par la formule :
, on peut généraliser le coefficient binomial à tous complexes s et t différents des entiers négatifs et tels que s - t ne soit pas un entier négatif, par la formule :On peut tenter d'unifier les définitions avec la fonction Gamma, en résolvant le problème de pôles de cette fonction par un passage à la limite :
Mais il faut prendre garde à l'ordre des limites qui ne peuvent commuter[1] et cette définition conduit à une valeur infinie du coefficient binomial dans les cas non étudiés précédemment
Formules faisant intervenir les coefficients binomiaux
On suppose que k, n sont des entiers ; z, z' des complexes.
Les formules suivantes peuvent être utiles :
-
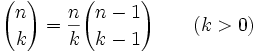 et plus généralement
et plus généralement 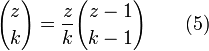 .
.
En remplaçant dans (3) x = y = 1, on obtient
En dérivant (3), et en remplaçant x = y = 1, il vient
En développant (
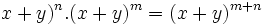 avec (3), on obtient l'identité de Vandermonde :
avec (3), on obtient l'identité de Vandermonde :-
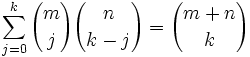 et plus généralement
et plus généralement 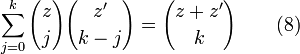
À partir du développement (8), en remplaçant m = k = n et en utilisant (4), on obtient
En développant
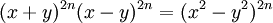 et en observant le coefficient devant
et en observant le coefficient devant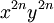 , on obtient
, on obtientOn a,
Ici, F(n+1) désigne le n+1 ième terme de la suite de Fibonacci. Cette formule sur les diagonales du triangle de Pascal peut être démontrée par une récurrence sur n en utilisant (2).
Et enfin,
Cela peut être démontré par récurrence sur n en utilisant (2).
Voir aussi
Notes et références
- ↑ John D. Cook, Binomial coefficients
Liens internes
- Arrangement
- Loi binomiale
- Loi binomiale négative
- loi multinomiale
- Formule du binôme généralisée
- Formule du binôme
- Portail des mathématiques
Catégories : Analyse combinatoire | Opération
Wikimedia Foundation. 2010.

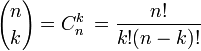

![\frac{n (n -1)(n - 2)\cdots (n - k +1)}{k!} = \begin{cases}\displaystyle \frac{n!}{k!(n-k)!} & \mbox{si } k \in [\![0;n]\!] \quad\mbox{(1)} \\\qquad 0 & \mbox{sinon}\end{cases}](/pictures/frwiki/50/2bedb307f01abef61af756bd866e4b1c.png)


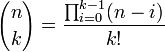

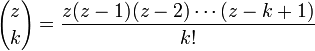
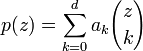

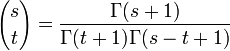
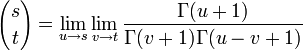
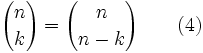
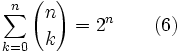
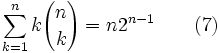

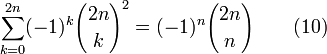
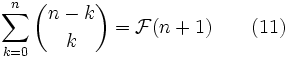
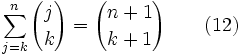




 Produit en couronne
Produit en couronne
 Somme connexe
Somme connexe

 Cup produit
Cup produit