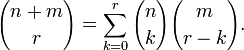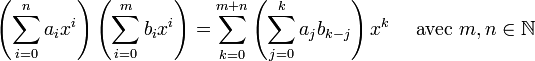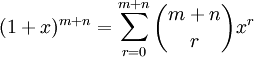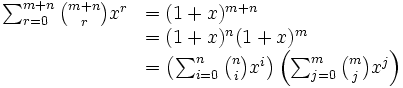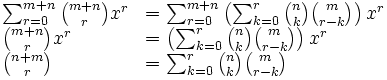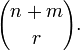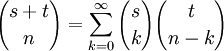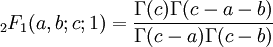Identite de Vandermonde

Identite de Vandermonde

Identité de Vandermonde

En mathématiques combinatoires, l'identité de Vandermonde, nommée d'après Alexandre-Théophile Vandermonde, affirme que

{n+m \choose r}=\sum_{k=0}^r{n \choose k}{m \choose r-k}.

Sommaire

Preuve

Algébrique

Elle peut être démontrée de façon algébrique.

Le produit de deux polynômes à une variable est donné par :

\left( \sum_{i=0}^n a_ix^i \right) \left( \sum_{i=0}^m b_ix^i \right) = \sum_{k=0}^{m+n} \left( \sum_{j=0}^k a_jb_{k-j} \right) x^k \quad\text{ avec } m, n \in \mathbb{N}

Par le théorème du binôme de Newton, nous savons que

(1+x)^{m+n} = \sum_{r=0}^{m+n} \binom{m+n}{r}x^r

Nous pouvons transformer cette égalité en produit de polynômes.

\begin{array}{ll} \sum_{r=0}^{m+n} \binom{m+n}{r}x^r & = (1+x)^{m+n} \\ & = (1+x)^{n} (1+x)^{m} \\ & = \left( \sum_{i=0}^{n} \binom{n}{i}x^i \right) \left( \sum_{j=0}^{m} \binom{m}{j}x^j \right) \end{array}

En utilisant l'équation du produit de polynômes plus haut et en simplifiant le résultat, l'identité de Vandermonde apparaît :

\begin{array}{ll} \sum_{r=0}^{m+n} \binom{m+n}{r}x^r & = \sum_{r=0}^{m+n} \left( \sum_{k=0}^{r} \binom{n}{k} \binom{m}{r-k} \right) x^r \\ \binom{m+n}{r}x^r & = \left( \sum_{k=0}^{r} \binom{n}{k} \binom{m}{r-k} \right) x^r \\ \binom{n+m}{r} & = \sum_{k=0}^{r} \binom{n}{k} \binom{m}{r-k} \end{array}

Bijective

Une preuve bijective est aussi possible. Supposons qu'un comité parlementaire soit composé de membres de deux partis politiques seulement, l'un comptant n membres, les « vert », l'autre m membres, les « jaunes ». Combien peut-on former de comités de taile r à partir de ces deux partis? La réponse est bien sûr

{n+m \choose r}.

Cette valeur est aussi donnée par la somme de toutes les valeurs de k du nombre de comités composé de k verts et r - k jaunes.

Distribution de probabilités hypergéométrique

Lorsque les deux côtés de cette identité sont divisés par l'expression à la gauche, alors les termes obtenus peuvent être interprétés comme des probabilités, lesquelles sont donnés par la distribution hypergéométrique. C'est la probabilité de tirer des billes rouges en r tirages sans remise d'une urne contenant n billes rouge et m billes bleu. Par exemple, supposons qu'une personne est responsable de créer un comité de r membres tirés au hasard parmi n verts et m jaune. Alors quelle est la probabilité qu'il y ait exactement k verts dans le comité ? La réponse se trouve dans cette distribution.

Identité de Chu-Vandermonde

L'identité de Chu-Vandermonde la généralise pour des valeurs non-entières :

{s+t \choose n}=\sum_{k=0}^\infty{s \choose k}{t \choose n-k}

Elle est vraie pour tous nombres complexes s et t.

Elle est un cas spécial du théorème hypergéométrique de Gauss qui affirme que

\;_2F_1(a,b;c;1) = \frac{\Gamma(c)\Gamma(c-a-b)}{\Gamma(c-a)\Gamma(c-b)}

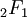où \;_2F_1 est la série hypergéométrique et Γ(n + 1) = n! est la fonction gamma. Il suffit d'appliquer a = -n et l'identité

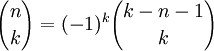{n\choose k} = (-1)^k {k-n-1 \choose k} à plusieurs reprises.

Lien externe

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Identit%C3%A9 de Vandermonde ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Identite de Vandermonde de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Identité De Vandermonde — En mathématiques combinatoires, l identité de Vandermonde, nommée d après Alexandre Théophile Vandermonde, affirme que Sommaire 1 Preuve 1.1 Algébrique …   Wikipédia en Français

  • Identité de vandermonde — En mathématiques combinatoires, l identité de Vandermonde, nommée d après Alexandre Théophile Vandermonde, affirme que Sommaire 1 Preuve 1.1 Algébrique …   Wikipédia en Français

  • Identité de Vandermonde — En mathématiques combinatoires, l identité de Vandermonde, nommée d après Alexandre Théophile Vandermonde (1772), affirme que Sommaire 1 Preuve 1.1 Algébrique 1.2 …   Wikipédia en Français

  • Identité de Chu-Vandermonde — Identité de Vandermonde En mathématiques combinatoires, l identité de Vandermonde, nommée d après Alexandre Théophile Vandermonde, affirme que Sommaire 1 Preuve 1.1 Algébrique …   Wikipédia en Français

  • Vandermonde — Alexandre Théophile Vandermonde Alexandre Théophile Vandermonde (parfois appelé Alexis Théophile), né à Paris le 28 février 1735 et mort à Paris le 1er janvier 1796, est un mathématicien français. Il fut aussi économiste, musicien… …   Wikipédia en Français

  • Alexandre-Theophile Vandermonde — Alexandre Théophile Vandermonde Alexandre Théophile Vandermonde (parfois appelé Alexis Théophile), né à Paris le 28 février 1735 et mort à Paris le 1er janvier 1796, est un mathématicien français. Il fut aussi économiste, musicien… …   Wikipédia en Français

  • Alexandre-Théophile Vandermonde — Naissance 28 février 1735 Paris (France) Décès 1er janvier 1796 (à 60 ans) Paris (France) Nationalité …   Wikipédia en Français

  • Matrice De Vandermonde — En algèbre linéaire, une matrice de Vandermonde est une matrice avec une progression géométrique dans chaque ligne. Elle tient son nom d Alexandre Théophile Vandermonde. Sommaire 1 Présentation 2 Inversibilité 3 Déterminant …   Wikipédia en Français

  • Matrice de vandermonde — En algèbre linéaire, une matrice de Vandermonde est une matrice avec une progression géométrique dans chaque ligne. Elle tient son nom d Alexandre Théophile Vandermonde. Sommaire 1 Présentation 2 Inversibilité 3 Déterminant …   Wikipédia en Français

  • Matrice de Vandermonde — En algèbre linéaire, une matrice de Vandermonde est une matrice avec une progression géométrique dans chaque ligne. Elle tient son nom du mathématicien français Alexandre Théophile Vandermonde. Sommaire 1 Présentation 2 Inversibilité 3… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”