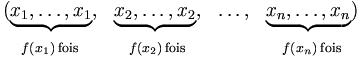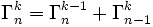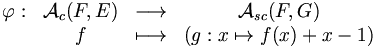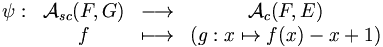Combinaison Avec Répétition

Combinaison avec répétition

Sommaire

1 Première approche
2 Une autre représentation
3 Nombre de combinaisons avec répétition
4 Une troisième démonstration (ensembliste)
5 Approche moins "matheuse" des combinaisons avec répétitions
6 Algorithme itératif de génération des Combinaisons avec répétition
7 Algorithme efficace de génération des Combinaisons avec répétition
8 Notes et références
9 Voir aussi
- 9.1 Articles connexes
- 9.2 Source

Première approche

En mathématiques, lorsque nous choisissons k objets parmi n objets discernables, chaque objet pouvant être répété (au plus k fois), nous obtenons un groupement non ordonné de k objets éventuellement répétés. Mais ce n’est pas acceptable en mathématiques de définir une k-combinaison avec répétition de cette façon, puisqu'un tel groupement n'est pas un ensemble (en effet la définition en extension d'un ensemble empêche la répétition des éléments et par exemple {1, 1, 2, 2, 2, 3}={1, 2, 3})..

Définition :

Une k-combinaison avec répétition d'un ensemble fini E de cardinal n, est une application f de E dans {0, 1, ..., k}, telle que

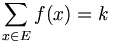$\sum_{x\in E}f(x)=k$ .

Plus précisément, si E={x₁, x₂, ..., x_n} alors f vérifie

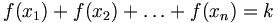$f(x_1)+f(x_2)+\ldots+f(x_n)=k$ .

f s'appelle aussi une combinaison de n éléments pris k à k.

Remarque :

Cette application indique pour chaque élément de E le nombre de fois qu'il est choisi; et si l'application associe la valeur 0 à un élément de E, alors l'élément n'est pas choisi. De plus la somme des nombres de répétitions doit bien être égale à k, si nous voulons exactement k objets éventuellement répétés.

Exemple :

Dans un jeu de dominos, un domino est une 2-combinaison avec répétition de l'ensemble E={blanc, 1, 2, 3, 4, 5, 6}. Chaque domino peut être représenté par une application de E dans {0, 1, 2} qui associe à chaque élément de E le nombre de fois où l'élément apparaît sur le domino.
Ainsi le domino blanc, est représenté par l'application f définie par

f(blanc)=2, f(1)=0, f(2)=0, f(3)=0, f(4)=0, f(5)=0 et f(6)=0

et le domino blanc, 1 par l'application f définie par

f(blanc)=1, f(1)=1, f(2)=0, f(3)=0, f(4)=0, f(5)=0 et f(6)=0

Une autre représentation

Soit n un entier naturel non nul, et soit l'ensemble E={x₁, x₂, ..., x_n}. Munissons E d'une relation d'ordre total et supposons que

x₁ < x₂ < ... < x_n

À une k-combinaison avec répétition de E, nous associons le k-uplet croissant (au sens large)

$\begin{matrix}(\underbrace{x_1, \ldots, x_1}, & \underbrace{x_2, \ldots, x_2}, & \ldots, & \underbrace{x_n, \ldots, x_n})\\{}_{f(x_1)\rm{\,fois}} & {}_{f(x_2)\rm{\,fois}} & & {}_{f(x_n)\rm{\,fois}}\end{matrix}$

Réciproquement à un k-uplet croissant d'éléments de E (a₁, a₂, ..., a_k), c'est-à-dire un k-uplet tel que

a₁ < a₂ < ... < a_k

nous pouvons associer l'application f:E → {0, 1, ..., k} qui envoie un élément de E sur le nombre de fois où il apparaît dans le k-uplet. Il est alors évident que

f(x₁)+f(x₂)+ ... +f(x_n)=k

et donc que f est une k-combinaison avec répétition de E.

Ainsi, il y a une bijection entre l'ensemble des k-combinaisons avec répétition de E et l'ensemble des k-uplets croissants d'éléments de E, ou encore des applications croissantes (au sens large) de {1, 2, ..., k} dans E.

'Exemple :

Un domino peut être représenté de manière unique par un couple croissant (a, b) tel que a ⩽ b d'éléments de E={blanc, 1, 2, 3, 4, 5, 6}.

Nombre de combinaisons avec répétition

Théorème :

Soit E un ensemble fini de cardinal n ( 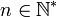$n \in \mathbb N^*$ ). Alors l'ensemble K_k(E) des k-combinaisons avec répétition de E est fini et son cardinal est égal à

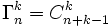$\Gamma_n^k=C_{n+k-1}^k$ ,

qui est le nombre de k-combinaisons de n+k-1 éléments.

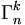$\Gamma_n^k$ se lit « Gamma nk ».

Démonstration :

Les combinaisons avec répétition sont des applications d'un ensemble fini dans un autre ensemble fini donc K_k(E) est fini. Supposons que E={x₁, x₂, ..., x_n}. L'ensemble K_k(E) se partitionne en l'ensemble $K'$ des combinaisons qui envoient x₁ sur 0 (représentées par un k-uplet croissant dans lequel x₁ n'apparaît pas) et l'ensemble 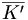$\overline{K'}$ des combinaisons qui envoient x₁ sur un entier naturel non nul (représentées par un k-uplet croissant dans lequel x₁ apparaît au moins une fois). En restreignant une combinaison de $K'$ à F=E\{x₁} (ce qui revient à la considérer comme un k-uplet croissant d'éléments de F), nous voyons qu'il y a autant d'éléments dans $K'$ que de combinaisons avec répétition de n-1 éléments pris k à k donc 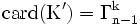$\rm{card}(K')=\Gamma_{n-1}^{k}$ . En retranchant 1 à la valeur en x₁ d'une combinaison de 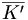$\overline{K'}$ (ce qui revient à « éliminer un x₁ » du k-uplet correspondant pour obtenir un (k-1)-uplet), nous transformons cette combinaison en une combinaison avec répétition de n éléments pris k-1 à k-1. 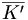Réciproquement, en ajoutant 1 à la valeur en x₁ d'une combinaison de n éléments pris k-1 à k-1, nous obtenons un élément de $\overline{K'}$ .
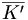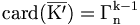Il y a donc autant d'éléments dans $\overline{K'}$ que de combinaisons avec répétition de n éléments pris k-1 à k-1 donc $\rm{card}(\overline{K'})=\Gamma_{n}^{k-1}$ .
En écrivant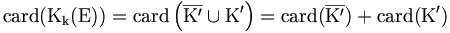

$\rm{card}(K_k(E))=\rm{card}\left(\overline{K'}\cup K'\right)=\rm{card}(\overline{K'})+\rm{card}(K')$ ,

nous obtenons la formule de récurrence

$\Gamma_n^k=\Gamma_n^{k-1}+\Gamma_{n-1}^k$

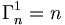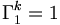De plus nous avons pour tout entier naturel n non nul, et pour tout entier naturel k $\Gamma_n^1=n$ et $\Gamma_1^k=1$ , et nous en déduisons le résultat.

Autre démonstration :

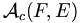Nous avons vu qu'il y avait une bijection entre l'ensemble des k-combinaisons avec répétition d'un ensemble E et l'ensemble des applications croissantes de F={1, 2, ..., k} dans E. Il suffit donc de déterminer le cardinal de ce dernier ensemble que nous noterons $\mathcal A_c(F, E)$ .

Théorème :

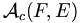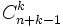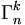Soient n et k deux entiers naturels non nuls, E un ensemble totalement ordonné fini de cardinal n, et F={1, 2, ..., k}. Alors l'ensemble $\mathcal A_c(F, E)$ des applications croissantes de F dans E est fini et son cardinal est le nombre de k-combinaisons avec répétition de E, égal à $C_{n+k-1}^k$ . Et ce cardinal se note $\Gamma_n^k$ .

Démonstration :

Sans perte de généralité, nous pouvons supposer que E={1, 2, ..., n}. Nous allons transformer une application croissante de F dans E en une application strictement croissante de F dans une autre ensemble G, en lui ajoutant l'application x ↦ x – 1.
Posons G={1, 2, ..., n+k-1} et notons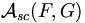 $\mathcal A_{sc}(F, G)$ l'ensemble des applications strictement croissantes de F dans G. À une application croissante f de F dans E, associons l'application g de F dans G définie par

∀ x ∈ F, g(x)=f(x)+x-1

Il est facile de vérifier que l'application

$\begin{matrix}\varphi : & \mathcal A_{c}(F, E) & \longrightarrow & \mathcal A_{sc}(F, G)\\& f & \longmapsto & (g: x\mapsto f(x)+x-1)\end{matrix}$

est bien définie. Et l'application

$\begin{matrix}\psi : & \mathcal A_{sc}(F, G) & \longrightarrow & \mathcal A_{c}(F, E)\\& f & \longmapsto & (g: x\mapsto f(x)-x+1)\end{matrix}$

est l'application réciproque de ϕ.

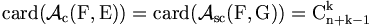D'où $\rm{card}(\mathcal A_{c}(F, E))=\rm{card}(\mathcal A_{sc}(F, G))=C_{n+k-1}^k$ .

Une troisième démonstration (ensembliste)

(P. LOUQUET, A. VOGT, Probabilités, Combinatoire, Statistiques, Armand Colin éd., 1971)

Notons 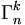$\Gamma_n^k$ le nombre de combinaisons avec répétition de k éléments pris parmi n.

Chacune de ces 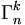$\Gamma_n^k$ combinaisons avec répétition s'écrit avec k éléments (répétés ou non). Si on les écrit in extenso, on utilisera donc k 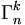$\Gamma_n^k$ éléments. Les n éléments jouant un rôle symétrique, chacun apparaîtra donc 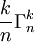$\frac{k}{n}\Gamma_n^k$ fois. Soit x l'un de ces éléments (apparaissant donc 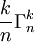$\frac{k}{n}\Gamma_n^k$ fois). (1) Calculons d'une autre manière le nombre de fois où il apparaît.

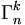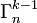Parmi les $\Gamma_n^k$ combinaisons avec répétition précédentes, le nombre de celles contenant x (une ou plusieurs fois) est : $\Gamma_n^{k-1}$ .

En effet, x étant imposé au moins une fois, on ne choisit plus que (k - 1) éléments, distincts ou non, sans ordre, mais toujours parmi n (car rien n'empêche que x soit répété et donc puisse réapparaître).

Chacune de ces 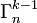$\Gamma_n^{k-1}$ combinaisons avec répétition contenant au moins une fois x, cela nous assure d'ores et déjà 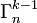$\Gamma_n^{k-1}$ apparitions de x. (2)

Enlevons à présent une fois x de chacune de ces 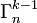$\Gamma_n^{k-1}$ combinaisons.

Chacune d'entre elles ne contient plus à présent que (k - 1) éléments (répétés ou non), il nous reste donc en tout 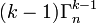$(k-1)\Gamma_n^{k-1}$ éléments. Nous n'avons plus d'hypothèse sur les (k - 1) éléments restants dans chaque combinaison avec répétition, chacun des n éléments joue donc un rôle symétrique et apparaît donc 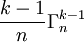$\frac{k-1}{n}\Gamma_n^{k-1}$ fois (en particulier x) (3).

Confrontons nos deux méthodes de calcul : nous avons donc : (1) = (2) + (3)

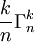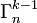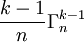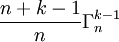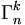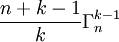Soit : $\frac{k}{n}\Gamma_n^k$ = $\Gamma_n^{k-1}$ + $\frac{k-1}{n}\Gamma_n^{k-1}$ = $\frac{n+k-1}{n}\Gamma_n^{k-1}$ Ce qui nous donne finalement : $\Gamma_n^k$ = $\frac{n+k-1}{k}\Gamma_n^{k-1}$ .

Par récurrence, on obtient donc, de proche en proche :

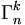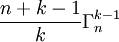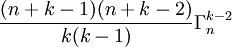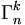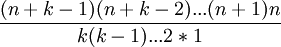
$\Gamma_n^k$ = $\frac{n+k-1}{k}\Gamma_n^{k-1}$ = $\frac{(n+k-1)(n+k-2)}{k(k-1)}\Gamma_n^{k-2}$ = ... Soit finalement : $\Gamma_n^k$ = $\frac{(n+k-1)(n+k-2)...(n+1)n}{k(k-1)...2*1}$

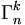On peut aussi écrire : $\Gamma_n^k$ = $\frac{produit-des-k-entiers-croissants-a-partir-de-n}{produit-des-k-entiers-croissants-a-partir-de-1}$

Ou encore, avec les factorielles : 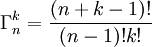$\Gamma_n^k=\frac{(n+k-1)!}{(n-1)!k!}$ Ou enfin, avec les coefficients binomiaux :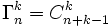 $\Gamma_n^k=C_{n+k-1}^k$

Approche moins "matheuse" des combinaisons avec répétitions

Une combinaison avec répétitions de "k" objets pris parmi "n" objets est une manière de sélectionner "k" objets parmi "n" objets distincts, sans tenir compte de l'ordre des "k" objets et avec répétitions, c’est-à-dire que le même objet peut être sélectionné plusieurs fois.

Le nombre de combinaisons avec répétitions de "k" objets pris parmi "n" objets égale :
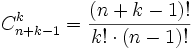
$C_{n+k-1}^k=\frac{(n+k-1)!}{k! \cdot (n-1)!}$

Voici deux démonstrations de cette affirmation.

Première démonstration :

Numérotons les "n" objets de 0 à (n-1).
Remarquez qu'à chaque combinaison avec répétitions de "k" objets parmi les "n", correspond une et une seule permutation avec répétitions de "n-1" boules noires et "k" boules blanches.
Le nombre de boules noires à gauche de la première boule blanche correspond au numéro d'un objet de la combinaison avec répétitions.
Le nombre de boules noires à gauche de la deuxième boule blanche correspond au numéro d'un objet de la combinaison avec répétitions.
etc. pour toutes les boules blanches.
Conclusion :
Le nombre de combinaisons avec répétitions de "k" objets pris parmi "n" objets égale le nombre de permutations avec répétitions de "k" boules blanches et de "n-1" boules noires.
Ce nombre vaut :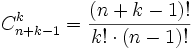 $C_{n+k-1}^k=\frac{(n+k-1)!}{k!\cdot(n-1)!}$
C'est le nombre de permutations des (n+k-1) boules, mais dans lesquelles on ne distingue pas les permutations des boules noires entre elles et des boules blanches entre elles.
On à (n+k-1)! permutations des boules, qu'il faut diviser par les (n-1)! permutations des boules noires et les k! permutations des boules blanches.

Deuxième démonstration :

Numérotons les "n" objets de 0 à (n-1).
Plaçons n boules noires numérotées de 0 à (n-1) et (k-1) boules blanches dans une urne.
Sur la première boule blanche est noté : "remplacez-moi par une boule noire identique à la plus à gauche".
Sur la deuxième boule blanche est noté : "remplacez-moi par une boule noire identique à la deuxième la plus à gauche".
Sur la troisième boule blanche est noté : "remplacez-moi par une boule noire identique à la troisième la plus à gauche".
etc.
On tire de l'urne "k" boules parmi les "n+k-1" boules noires et blanches. On les place par ordre des numéros sur les boules.
Le nombre de résultats possibles de l'expérience précédente est égal au nombre de combinaisons avec répétitions de "k" objets pris parmi "n" objets.
Il est également égal au nombre de combinaisons sans répétitions de "k" boules parmi les "n+k-1" boules noires et blanches.

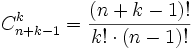
Ce nombre est : $C_{n+k-1}^k=\frac{(n+k-1)!}{k!\cdot(n-1)!}$

Algorithme itératif de génération des Combinaisons avec répétition

generer_k_combinaison(n,k): // k objets pris parmi n objets sans ordre et avec répétition
  declarer tab[n] <-- {k,0,0......}
  tant que tab[n] != k:
    afficher (tab)
    si tab[n] != 0
         tmp <-- tab[n]
         tab[n] <-- 0
         i <-- indice de la derniere case non nulle de tab
         tab[i] <-- tab[i] - 1
         tab[i+1] <-- tmp + 1
    sinon
         i <-- indice de la derniere case non nulle de tab
         tab[i] <-- tab[i] - 1
         tab[i+1]  <-- 1
    fin si
  fin tant que
  afficher (tab)
fin

Une implémentation en C:

#include <stdio.h>
#define MAX 256
int NB;
void afficher(int *t, int l) {
    int i,j;
    for (i = 0; i < l; i++) printf("%d ",t[i]);
    printf("[ ");
    for (i = 0; i < l; i++) {
        for (j = 0; j < t[i]; j++) {
            printf("%d ", i);
        }
    }
    printf("]\n");
    NB++;
}
 
void kcombinaison(int *t, int n, int p, void (*func)(int*,int)) {
    int tmp,i;
    t[0] = p;
    memset(t+1,0, sizeof *t * (n - 1));
    while(t[n-1] != p) {
        func(t,n);
 
        tmp = t[n-1];
        t[n-1] = 0;
        i = n-1;
        while(t[i] == 0) i--;
 
        t[i]--;
        t[i+1] = tmp + 1;
    }
    func(t,n);
}
 
int main() {
    int tab[MAX];
    int n = 3, p = 4; // 4 objets pris parmi 3
    NB = 0;
    kcombinaison(tab,n,p,afficher);
    printf("\n");
    printf("le NOMBRE de facon de prendre %d objets parmi %d sans ordre et avec repetition est: \n C(%d,%d) = %d\n", p, n, n+p-1, p, NB);
    return 0;
}

Algorithme efficace de génération des Combinaisons avec répétition

Le plus efficace, et le plus simple, pour calculer le nombre de combinaisons avec répétitions est encore d'utiliser l'algorithme calculant le nombre de combinaisons sans répétitions, comme décrit sur la page Combinaison. En effet, comme indiqué plus haut le nombre de combinaisons de "k" objets parmi "n" avec répétitions est le même que le nombre de combinaisons de "k" objets parmi "n+k-1" sans répétitions. En Ocaml et avec des entiers sur 64 bits, l'implémentation est la suivante :

open Int64;;                                          (* Chargement du module de calcul arithmétique sur 64 bits (marche aussi sur machines 32 bits) *)
let kcombinaison (n : int64) (k : int64) : int64 =    (* Deux arguments, n et k, de type entiers signés sur 64 bits                                  *)
   let n = sub (add n k) 1L in                        (* n devient n+k-1. Toute la suite correspond au calcul du nb de combinaisons sans répétitions *)
   let nk = sub n k in                                (* Calcul de nk = n - k pour éviter de le refaire trop souvent                                 *)
   let (k,nk) = if k<nk then (k,nk) else (nk,k)       (* Ce calcul est symétrique selon k ou nk, donc on calcule pour le plus facile/petit des deux  *)
   let i = ref 1L and r = ref 1L in                   (* Initialisation de notre compteur "i", et de "r" pour stoquer le résultat intermédiaire      *)
   while !i <= k do
      r := div (mul !r (add nk !i)) !i;               (* Les propriétés du nb de combinaisons garantissent que toutes ces divisions sont sans reste  *)
      i := succ !i;
   done; !r                                           (* Il ne reste plus qu'à rendre le résultat final                                              *)
;;

Ceci permet de calculer par exemple le nombre de k-combinaisons de 20 parmi 40, qui ne peut pas être représenté en 32 bits ni calculé par l'algorithme itératif:

# kcombinaison 40L 20L;;
- : int64 = 2794563003870330L

Notes et références

Voir aussi

Source

P. LOUQUET, A. VOGT, Probabilités, Combinatoire, Statistiques, Armand Colin éd., 1971

Portail des mathématiques

Ce document provient de « Combinaison avec r%C3%A9p%C3%A9tition ».

Catégorie : Analyse combinatoire

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Combinaison Avec Répétition de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Combinaison avec repetition — Combinaison avec répétition Sommaire 1 Première approche 2 Une autre représentation 3 Nombre de combinaisons avec répétition 4 Une troisième dé … Wikipédia en Français
Combinaison avec répétition — Dans le domaine des dénombrements (mathématiques), une combinaison avec répétition est une combinaison où donc l ordre des éléments n importe pas et où, contrairement à une combinaison classique, chaque élément de la combinaison peut apparaître… … Wikipédia en Français
Permutation avec repetition — Permutation avec répétition En mathématiques, les permutations avec répétition d objets dont certains sont indifférenciés sont les divers groupements ordonnés de tous ces objets. Par exemple, 112, 121 et 211 pour deux chiffres 1 et un chiffre 2.… … Wikipédia en Français
Permutation avec répétition — En mathématiques, les permutations avec répétition d objets dont certains sont indifférenciés sont les divers groupements ordonnés de tous ces objets. Par exemple, 112, 121 et 211 pour deux chiffres 1 et un chiffre 2. Lorsque nous permutons n… … Wikipédia en Français
combinaison — [ kɔ̃binɛzɔ̃ ] n. f. • 1669; altér. de combination (1361); bas lat. combinatio, de combinare « combiner » 1 ♦ Assemblage (d éléments) dans un arrangement déterminé. ⇒ arrangement. Combinaison de couleurs, de lignes. ⇒ composition, disposition,… … Encyclopédie Universelle
Combinaison (Mathématiques) — Pour les articles homonymes, voir combinaison. En mathématiques, lorsque nous choisissons k objets parmi n objets discernables (numérotés de 1 à n) et que l’ordre dans lequel les objets sont placés (ou énumérés) n’a pas d’importance, nous pouvons … Wikipédia en Français
Combinaison (mathematiques) — Combinaison (mathématiques) Pour les articles homonymes, voir combinaison. En mathématiques, lorsque nous choisissons k objets parmi n objets discernables (numérotés de 1 à n) et que l’ordre dans lequel les objets sont placés (ou énumérés) n’a… … Wikipédia en Français
Combinaison (homonymie) — Combinaison Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Combinaison (mathématiques) — Pour les articles homonymes, voir combinaison. En mathématiques, lorsque nous choisissons k objets parmi n objets discernables (numérotés de 1 à n) et que l’ordre dans lequel les objets sont placés (ou énumérés) n’a pas d’importance, nous pouvons … Wikipédia en Français
Combinaison — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Combinaison », sur le Wiktionnaire (dictionnaire universel) Une combinaison peut être : un objet… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Combinaison Avec Répétition