- Transformation d'Abel
-
Sommation par parties
La sommation par parties est l'équivalent pour les séries de l'intégration par parties. On l'appelle également transformation d'Abel ou sommation d'Abel.
Sommaire
Méthode
Soient deux suites
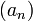 et
et 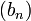 , avec
, avec 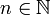 . On considère la série suivante :
. On considère la série suivante :

Si on pose
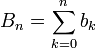 ,
,
alors pour tout n>0,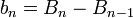
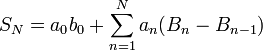
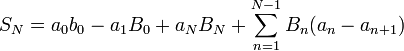
On obtient finalement l'égalité suivante :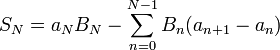
Cette opération, qui transforme l'expression de la série à étudier, est utile pour prouver certains critères de convergence de
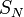 .
.Similitude avec l'intégration par parties
La formule de l'intégration s'écrit :
![\int_a^b f(x) g'(x)\,dx = \left[ f(x) g(x) \right]_{a}^{b} - \int_a^b f'(x) g(x)\,dx](/pictures/frwiki/48/0cc4450e2b913b0d32c34fac3ec1aea3.png)
Si on laisse de côté les conditions aux limites, on s'aperçoit que l'intégration par parties consiste à intégrer une des deux fonctions présentes dans l'intégrale initiale (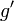 devient
devient 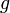 ) et à dériver l'autre (
) et à dériver l'autre ( devient
devient 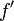 ).
).La sommation par parties consiste en une opération analogue dans le domaine discret, puisque l'une des deux séries est sommée (
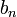 devient
devient 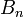 ) et l'autre est différenciée (
) et l'autre est différenciée (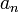 devient
devient 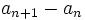 ).
).On peut considérer la formule sommatoire d'Abel comme une généralisation de ces deux formules.
Applications
On se place par la suite dans le cas où
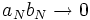 , car sinon on sait que
, car sinon on sait que 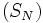 est grossièrement divergente.
est grossièrement divergente.Si
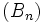 est bornée par un réel M et que
est bornée par un réel M et que 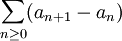 est une série absolument convergente, alors la série
est une série absolument convergente, alors la série 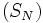 est convergente.
est convergente.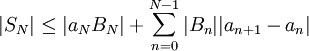
La somme de la série vérifie par ailleurs l'inégalité :
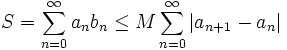
Exemples
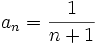 et
et 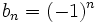
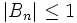 et
et 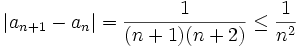
On sait que la série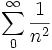 converge (voir fonction zêta de Riemann), donc les conditions exposées ci-dessus sont toutes réunies.
converge (voir fonction zêta de Riemann), donc les conditions exposées ci-dessus sont toutes réunies.
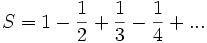 converge.
converge.
NB: Cet exemple peut également être prouvé grâce au critère de convergence des séries alternées.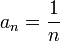 et
et 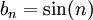
(Nous ne définissons ici la somme qu'à partir du rang n=1 au lieu de n=0, mais cela n'affecte en rien l'existence de la limite de la série.)
Comme précédemment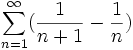 converge absolument, et
converge absolument, et 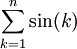 est bornée d'après l'expression du noyau de Dirichlet.
est bornée d'après l'expression du noyau de Dirichlet.
Par conséquent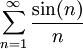 converge.
converge.- La sommation par parties sert dans la preuve du théorème d'Abel.
- Portail des mathématiques
Catégorie : Série
Wikimedia Foundation. 2010.
