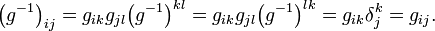Inverse de la matrice du tenseur metrique

Inverse de la matrice du tenseur metrique

Inverse de la matrice du tenseur métrique

Étant donné un système de coordonnées, la matrice du tenseur métrique en composantes contravariantes gij est la matrice inverse de la matrice du tenseur métrique en composantes covariantes :

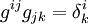g^{ij}g_{jk} = \delta^i_k.

Autrement dit, le tenseur métrique est son propre inverse.

Démonstration

On a défini (cf. transformation contraco) le tenseur métrique inverse (g − 1)ij comme l'inverse de gij. En faisant intervenir deux fois le tenseur métrique, on obtient son expression covariante

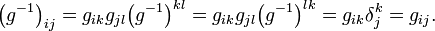
\bigl(g^{-1}\bigr)_{ij} = g_{ik} g_{jl} \bigl(g^{-1}\bigr)^{kl} = g_{ik} g_{jl} \bigl(g^{-1}\bigr)^{lk} = g_{ik} \delta^k_j = g_{ij}.

∎Le tenseur métrique est donc son propre inverse, c.q.f.d.

Ce document provient de « Inverse de la matrice du tenseur m%C3%A9trique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Inverse de la matrice du tenseur metrique de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Inverse De La Matrice Du Tenseur Métrique — Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel …   Wikipédia en Français

  • Inverse de la matrice du tenseur métrique — Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel …   Wikipédia en Français

  • Tenseur metrique — Tenseur métrique Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel …   Wikipédia en Français

  • Tenseur métrique — En géométrie et plus particulièrement en géométrie différentielle, le tenseur métrique est un tenseur d ordre 2 qui est utilisé pour la mesure des distances et des angles. Il généralise le théorème de Pythagore. Dans un système de coordonnées… …   Wikipédia en Français

  • Tenseur energie-impulsion — Tenseur énergie impulsion Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace… …   Wikipédia en Français

  • Tenseur énergie impulsion — Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel …   Wikipédia en Français

  • Tenseur de Maxwell — Tenseur électromagnétique Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace… …   Wikipédia en Français

  • Tenseur de champ électromagnétique — Tenseur électromagnétique Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace… …   Wikipédia en Français

  • Tenseur electromagnetique — Tenseur électromagnétique Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace… …   Wikipédia en Français

  • Tenseur — En mathématiques, plus précisément en algèbre multilinéaire et en géométrie différentielle, un tenseur désigne un objet très général, dont la valeur s exprime dans un espace vectoriel. On peut l utiliser entre autres pour représenter des… …   Wikipédia en Français

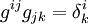Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”