- Torsion
-
Pour les articles homonymes, voir Torsion (homonymie).
Moments de force résultant de l'action d'un couple de forces dans deux plans parallèles
La torsion est la sollicitation subie par un corps soumis à l'action d'un couple de forces opposées agissant dans des plans parallèles et dont l'élément de réduction est un moment de force agissant dans l'axe de la poutre. La théorie des poutres décrit cette sollicitation de manière plus précise.
La balance de torsion est un appareil servant à mesurer l'intensité de petites forces au moyen du couple de torsion d'un fil métallique.
Un ressort de torsion est une tige soumise à des efforts de torsion et pouvant accepter de grandes déformations.
La barre de torsion est un ressort de torsion peu déformable constitué d'une barre métallique. Les barres de torsion sont notamment utilisées pour la suspension de véhicules automobiles.
Sommaire
Torsion en théorie des poutres
Torsion uniforme d'un arbre circulaire
Répartition des contraintes sur l'axe vertical dans le cas d'un arbre plein (gauche) et d'un tube (droite).Selon la théorie d'Euler-Bernoulli, si l'on reste en petites déformations, le moment de torsion Mt crée des contraintes de cisaillement τ qui sont proportionnelle à la distance r par rapport à l'axe de torsion :
où
- Mt est le moment de torsion ;
- IG est le moment quadratique de torsion, dépendant de la forme de la section (diamètre extérieur, et diamètre intérieur dans le cas d'un tube).
Pour un arbre plein, on a
où D est le diamètre. Pour un tube, on soustrait simplement le moment quadratique de la partie évidée :
où D est le diamètre extérieur et d est le diamètre intérieur.
Article détaillé : Moment quadratique.La contrainte de cisaillement maximale vaut
où v est le rayon extérieur de la pièce (D/2). La quantité (IG/v ) est appelée module de torsion.
Unités Grandeur Unité
internationaleUnité
usuelleUnité pour
les calculsMt Nm Nm Nmm IG m4 cm4 mm4 v m mm mm (IG/v ) m3 cm3 mm3 τ Pa MPa MPa Torsion non uniforme
La torsion s'exprime sous la forme d'un moment de torsion Mx agissant dans l'axe de la poutre. Sous l'effet de la torsion, les sections transversales de la poutre ne restent généralement pas planes (on doit abandonner l'hypothèse de Bernoulli) ; on dit qu'elles gauchissent. Lorsque leur gauchissement est libre, seules des contraintes tangentielles τv apparaissent et la poutre n'est soumise qu'à de la torsion uniforme (ou torsion de Saint-Venant).
Lorsque leur gauchissement est empêché (par exemple par un encastrement en rotation) ou que le moment de torsion n'est pas constant (provoquant un gauchissement variable d'une section transversale à l'autre), des contraintes normales σw apparaissent en plus des contraintes de cisaillement et la barre est soumise à de la torsion non uniforme.
La torsion non uniforme est toujours accompagnée de la torsion uniforme. Le moment de torsion Mx peut donc se décomposer en la somme d'une part uniforme Mv et d'une part non uniforme Mw.
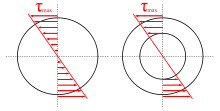
Une section fermée ou trapue (compacte) travaille principalement en torsion uniforme ; dans le cas d'une poutre dont la section présente une symétrie de révolution (section circulaire ou annulaire par exemple), les contraintes de cisaillement varient de manière linéaire lorsque l'on s'éloigne de la fibre neutre.
Les sections ouvertes ou sans symétrie de révolution travaillent principalement en torsion non uniforme et le problème est plus complexe. En particulier, la contrainte à une surface libre (qui n'est pas en contact avec une autre pièce) est nécessairement dans le plan tangent à cette surface, et notamment la contrainte à un angle libre est nécessairement nulle.
Lorsqu'aucune part de torsion n'est prédominante, on parle de torsion mixte ; c'est le cas notamment des profilés laminés.
Voir aussi
Wikimedia Foundation. 2010.
