Réseau de neurones artificiels

 Pour l’article homonyme, voir Réseau de neurones (biologie). 

Pour les articles homonymes, voir Réseau.

Un réseau de neurones artificiels est un modèle de calcul dont la conception est très schématiquement inspirée du fonctionnement des neurones biologiques.
Les réseaux de neurones sont généralement optimisés par des méthodes d’apprentissage de type probabiliste, en particulier bayésiens. Ils sont placés d’une part dans la famille des applications statistiques, qu’ils enrichissent avec un ensemble de paradigmes ^[1] permettant de générer des classifications rapides (réseaux de Kohonen en particulier), et d’autre part dans la famille des méthodes de l’intelligence artificielle auxquelles ils fournissent un mécanisme perceptif indépendant des idées propres de l'implémenteur, et fournissant des informations d'entrée au raisonnement logique formel.
En modélisation des circuits biologiques, ils permettent de tester quelques hypothèses fonctionnelles issues de la neurophysiologie, ou encore les conséquences de ces hypothèses pour les comparer au réel.

Historique

Vue simplifiée d'un réseau artificiel de neurones

Les réseaux neuronaux sont construits sur un paradigme biologique, celui du neurone formel (comme les algorithmes génétiques le sont sur la sélection naturelle). Ces types de métaphores biologiques sont devenues courantes avec les idées de la cybernétique et biocybernétique. Celui-ci ne prétend pas davantage décrire le cerveau qu'une aile d'avion, par exemple, copier celle d'un oiseau. En particulier le rôle des cellules gliales n'est pas simulé pour le moment (2010).

Les neurologues Warren McCulloch et Walter Pitts publièrent dès la fin des années 1950 les premiers travaux sur les réseaux de neurones, avec un article fondateur : What the frog’s eye tells to the frog’s brain^[2]. Ils constituèrent ensuite un modèle simplifié de neurone biologique communément appelé neurone formel. Ils montrèrent que des réseaux de neurones formels simples peuvent théoriquement réaliser des fonctions logiques, arithmétiques et symboliques complexes.

Le neurone formel est conçu comme un automate doté d'une fonction de transfert qui transforme ses entrées en sortie selon des règles précises. Par exemple, un neurone somme ses entrées, compare la somme résultante à une valeur seuil, et répond en émettant un signal si cette somme est supérieure ou égale à ce seuil (modèle ultra-simplifié du fonctionnement d'un neurone biologique). Ces neurones sont par ailleurs associés en réseaux dont la topologie des connexions est variable : réseaux proactifs, récurrents, etc. Enfin, l'efficacité de la transmission des signaux d'un neurone à l'autre peut varier : on parle de « poids synaptique », et ces poids peuvent être modulés par des règles d'apprentissage (ce qui mime la plasticité synaptique des réseaux biologiques).

Une fonction des réseaux de neurones formels, à l’instar du modèle vivant, est d'opérer rapidement des classifications et d'apprendre à les améliorer. À l’opposé des méthodes traditionnelles de résolution informatique, on ne doit pas construire un programme pas à pas en fonction de la compréhension de celui-ci. Les paramètres importants de ce modèle sont les coefficients synaptiques et le seuil de chaque neurone, et la façon de les ajuster. Ce sont eux qui déterminent l'évolution du réseau en fonction de ses informations d'entrée. Il faut choisir un mécanisme permettant de les calculer et de les faire converger si possible vers une valeur assurant une classification aussi proche que possible de l'optimale. C’est ce qu'on nomme la phase d’apprentissage du réseau. Dans un modèle de réseaux de neurones formels, apprendre revient donc à déterminer les coefficients synaptiques le moins mal adaptés à classifier les exemples présentés.

Les travaux de McCulloch et Pitts n’ont pas donné d’indication sur une méthode pour adapter les coefficients synaptiques. Cette question au cœur des réflexions sur l’apprentissage a connu un début de réponse grâce aux travaux du physiologiste canadien Donald Hebb sur l’apprentissage en 1949 décrits dans son ouvrage The Organization of Behaviour. Hebb a proposé une règle simple qui permet de modifier la valeur des coefficients synaptiques en fonction de l’activité des unités qu’ils relient. Cette règle aujourd’hui connue sous le nom de « règle de Hebb » est presque partout présente dans les modèles actuels, même les plus sophistiqués.

Réseau de neurones avec rétroaction

À partir de cet article, l’idée se sema au fil du temps dans les esprits, et elle germa dans l’esprit de Franck Rosenblatt en 1957 avec le modèle du perceptron. C’est le premier système artificiel capable d’apprendre par expérience, y compris lorsque son instructeur commet quelques erreurs (ce en quoi il diffère nettement d’un système d’apprentissage logique formel).

En 1969, un coup grave fut porté à la communauté scientifique gravitant autour des réseaux de neurones : Marvin Lee Minsky et Seymour Papert publièrent un ouvrage mettant en exergue quelques limitations théoriques du Perceptron, et plus généralement des classifieurs linéaires, notamment l’impossibilité de traiter des problèmes non linéaires ou de connexité. Ils étendirent implicitement ces limitations à tous modèles de réseaux de neurones artificiels. Paraissant alors dans une impasse, la recherche sur les réseaux de neurones perdit une grande partie de ses financements publics, et le secteur industriel s’en détourna aussi. Les fonds destinés à l’intelligence artificielle furent redirigés plutôt vers la logique formelle et la recherche piétina pendant dix ans^[3]. Cependant, les solides qualités de certains réseaux de neurones en matière adaptative (e.g. Adaline), leur permettant de modéliser de façon évolutive des phénomènes eux-mêmes évolutifs, les amèneront à être intégrés sous des formes plus ou moins explicites dans le corpus des systèmes adaptatifs; utilisés dans le domaine des télécommunications ou celui du contrôle de processus industriels.

En 1982, John Joseph Hopfield, physicien reconnu, donna un nouveau souffle au neuronal en publiant un article introduisant un nouveau modèle de réseau de neurones (complètement récurrent). Cet article eut du succès pour plusieurs raisons, dont la principale était de teinter la théorie des réseaux de neurones de la rigueur propre aux physiciens. Le neuronal redevint un sujet d’étude acceptable, bien que le modèle de Hopfield souffrît des principales limitations des modèles des années 1960, notamment l’impossibilité de traiter les problèmes non-linéaires.

À la même date, les approches algorithmiques de l’intelligence artificielle furent l’objet de désillusion, leurs applications ne répondant pas aux attentes. Cette désillusion motiva une réorientation des recherches en intelligence artificielle vers les réseaux de neurones (bien que ces réseaux concernent la perception artificielle plus que l’intelligence artificielle à proprement parler). La recherche fut relancée et l’industrie reprit quelque intérêt au neuronal (en particulier pour des applications comme le guidage de missiles de croisière). En 1984 (?), c’est le système de rétropropagation du gradient de l’erreur qui est le sujet le plus débattu dans le domaine.

Une révolution survient alors dans le domaine des réseaux de neurones artificiels : une nouvelle génération de réseaux de neurones, capables de traiter avec succès des phénomènes non-linéaires : le perceptron multicouche ne possède pas les défauts mis en évidence par Marvin Minsky. Proposé pour la première fois par Werbos, le Perceptron Multi-Couche apparait en 1986 introduit par Rumelhart, et, simultanément, sous une appellation voisine, chez Yann le Cun. Ces systèmes reposent sur la rétropropagation du gradient de l’erreur dans des systèmes à plusieurs couches, chacune de type Adaline de Bernard Widrow, proche du Perceptron de Rumelhart.

Les réseaux de neurones ont par la suite connu un essor considérable, et ont fait partie des premiers systèmes à bénéficier de l’éclairage de la théorie de la « régularisation statistique » introduite par Vladimir Vapnik en Union soviétique et popularisée en occident depuis la chute du mur. Cette théorie, l’une des plus importantes du domaine des statistiques, permet d’anticiper, d’étudier et de réguler les phénomènes liés au sur-apprentissage. On peut ainsi réguler un système d’apprentissage pour qu’il arbitre au mieux entre une modélisation pauvre (exemple : la moyenne) et une modélisation trop riche qui serait optimisée de façon illusoire sur un nombre d’exemples trop petit, et serait inopérant sur des exemples non encore appris, même proches des exemples appris. Le sur-apprentissage est une difficulté à laquelle doivent faire face tous les systèmes d’apprentissage par l’exemple, que ceux-ci utilisent des méthodes d’optimisation directe (e.g. régression linéaire), itératives (e.g., l'algorithme du gradient), ou itératives semi-directes (gradient conjugué, espérance-maximisation...) et que ceux-ci soient appliqués aux modèles statistiques classiques, aux modèles de Markov cachés ou aux réseaux de neurones formels.

Utilité

Les réseaux de neurones, en tant que système capable d'apprendre, mettent en œuvre le principe de l'induction, c’est-à-dire l'apprentissage par l'expérience. Par confrontation avec des situations ponctuelles, ils infèrent un système de décision intégré dont le caractère générique est fonction du nombre de cas d'apprentissages rencontrés et de leur complexité par rapport à la complexité du problème à résoudre. Par opposition, les systèmes symboliques capables d'apprentissage, s'ils implémentent également l'induction, le font sur base de la logique algorithmique, par complexification d'un ensemble de règles déductives (ex : prolog).

Grâce à leur capacité de classification et de généralisation, les réseaux de neurones sont généralement utilisés dans des problèmes de nature statistique, tels que la classification automatique de codes postaux ou la prise de décision concernant un achat boursier en fonction de l'évolution des cours. Autre exemple, une banque peut générer un jeu de données sur les clients qui ont effectué un emprunt constituées : de leur revenu, de leur âge, du nombre d’enfants à charge… et s’il s’agit d’un bon client. Si ce jeu de données est suffisamment grand, il peut être utilisé pour l’entraînement d’un réseau de neurones. La banque pourra alors présenter les caractéristiques d’un potentiel nouveau client, et le réseau répondra s’il sera bon client ou non, en généralisant à partir des cas qu’il connaît.

Si le réseau de neurones fonctionne avec des nombres réels, la réponse traduit une probabilité de certitude. Par exemple : 1 pour « sûr qu’il sera un bon client », -1 pour « sûr qu’il sera mauvais client », 0 pour « aucune idée », 0,9 pour « presque sûr qu’il sera bon client ».

Le réseau de neurones ne fournit pas toujours de règle exploitable par un humain. Le réseau reste souvent une boîte noire qui fournit une réponse quand on lui présente une donnée, mais le réseau ne fournit pas de justification facile à interpréter.

Les réseaux de neurones sont réellement utilisés, par exemple :

• pour la classification d’espèces animales par espèce étant donnée une analyse ADN.
• reconnaissance de motif ; par exemple pour la Reconnaissance optique de caractères (OCR), et notamment par les banques pour vérifier le montant des chèques, par La Poste pour trier le courrier en fonction du code postal, etc. ; ou bien encore pour le déplacement automatisé de robots mobiles autonomes.
• approximation d’une fonction inconnue.
• modélisation accélérée d’une fonction connue mais très complexe à calculer avec exactitude ; par exemple certaines fonctions d’inversions utilisées pour décoder les signaux de télédétection émis par les satellites et les transformer en données sur la surface de la mer.
• estimations boursières :
  • apprentissage de la valeur d’une entreprise en fonction des indices disponibles : bénéfices, endettements à long et court terme, chiffre d’affaires, carnet de commandes, indications techniques de conjoncture. Ce type d’application ne pose pas en général de problème
  • tentatives de prédiction sur la périodicité des cours boursiers. Ce type de prédiction est très contesté pour deux raisons, l’une étant qu'il n'est pas évident que le cours d’une action ait de façon tout à fait convaincante un caractère périodique (le marché anticipe en effet largement les hausses comme les baisses prévisibles, ce qui applique à toute périodicité éventuelle une variation de période tendant à la rendre difficilement fiable), et l’autre que l’avenir prévisible d’une entreprise détermine au moins aussi fortement le cours de son action, si ce n'est plus encore que peut le faire son passé ; les cas de Pan Am, Manufrance ou IBM permettent de s’en convaincre.
• modélisation de l'apprentissage et amélioration des techniques de l'enseignement.
• en météorologie, pour la classification de conditions atmosphériques et la prévision statistique du temps.

Limites

• Les réseaux de neurones artificiels ont besoin de cas réels servant d’exemples pour leur apprentissage (on appelle cela la base d'apprentissage). Ces cas doivent être d’autant plus nombreux que le problème est complexe et que sa topologie est peu structurée. Par exemple, on peut optimiser un système neuronal de lecture de caractères en utilisant le découpage manuel d’un grand nombre de mots écrits à la main par de nombreuses personnes. Chaque caractère peut alors être présenté sous la forme d’une image brute, disposant d’une topologie spatiale à deux dimensions, ou d’une suite de segments presque tous liés. La topologie retenue, la complexité du phénomène modélisé, et le nombre d’exemples doivent être en rapport. Sur un plan pratique, cela n’est pas toujours facile car les exemples peuvent être soit en quantité absolument limitée ou trop onéreux à collecter en nombre suffisant.

• Il y a des problèmes qui se traitent bien avec les réseaux de neurones, en particulier ceux de classification en domaines convexes (c’est-à-dire tels que si des points A et B font partie du domaine, alors tout le segment AB en fait partie aussi). Des problèmes comme "Le nombre d’entrées à 1 (ou à zéro) est-il pair ou impair ?" se résolvent en revanche très mal : pour affirmer de telles choses sur 2 puissance N points, si on se contente d’une approche naïve mais homogène, il faut précisément N-1 couches de neurones intermédiaires, ce qui nuit à la généralité du procédé.

• Un exemple caricatural, mais significatif est le suivant : disposant en entrée du seul poids d'une personne, le réseau doit déterminer si cette personne est une femme ou un bien un homme. Les femmes étant statistiquement un peu plus légères que les hommes, le réseau fera toujours un peu mieux qu'un simple tirage au hasard : cet exemple dépouillé indique la simplicité et les limitations de ces modèles mais il montre également comment l'étendre : L'information "port d'une jupe", si on l'ajoute, aurait clairement un coefficient synaptique plus grand que la simple information de poids.

Modèle

Structure du réseau

Structure d'un neurone artificiel. Le neurone calcule la somme de ses entrées puis cette valeur passe à travers la fonction d'activation pour produire sa sortie.

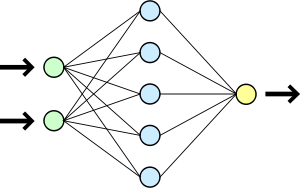
Un réseau de neurones est en général composé d'une succession de couches dont chacune prend ses entrées sur les sorties de la précédente. Chaque couche (i) est composée de Ni neurones, prenant leurs entrées sur les Ni-1 neurones de la couche précédente. À chaque synapse est associée un poids synaptique, de sorte que les Ni-1 sont multipliés par ce poids, puis additionnés par les neurones de niveau i, ce qui est équivalent à multiplier le vecteur d'entrée par une matrice de transformation. Mettre l'une derrière l'autre les différentes couches d'un réseau de neurones reviendrait à mettre en cascade plusieurs matrices de transformation et pourrait se ramener à une seule matrice, produit des autres, s'il n'y avait à chaque couche, la fonction de sortie qui introduit une non linéarité à chaque étape. Ceci montre l'importance du choix judicieux d'une bonne fonction de sortie : un réseau de neurones dont les sorties seraient linéaires n'aurait aucun intérêt.

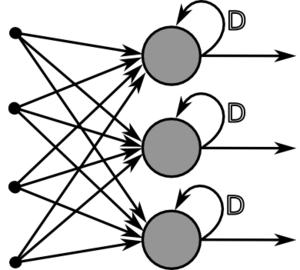
Au-delà de cette structure simple, le réseau de neurones peut également contenir des boucles qui en changent radicalement les possibilités mais aussi la complexité. De la même façon que des boucles peuvent transformer une logique combinatoire en logique séquentielle, les boucles dans un réseau de neurones transforment un simple dispositif de reconnaissance d'entrées en une machine complexe capable de toute sortes de comportements.

Fonction de combinaison

Considérons un neurone quelconque.

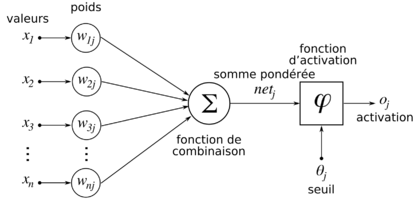
Il reçoit des neurones en amont un certain nombre de valeurs via ses connexions synaptiques, et il produit une certaine valeur en utilisant une fonction de combinaison. Cette fonction peut donc être formalisée comme étant une fonction vecteur-à-scalaire, notamment :

• Les réseaux de type MLP (Multi-Layer Perceptron) calculent une combinaison linéaire des entrées, c’est-à-dire que la fonction de combinaison renvoie le produit scalaire entre le vecteur des entrées et le vecteur des poids synaptiques.
• Les réseaux de type RBF (Radial Basis Function) calculent la distance entre les entrées, c’est-à-dire que la fonction de combinaison renvoie la norme euclidienne du vecteur issu de la différence vectorielle entre les vecteurs d’entrées.

Fonction d’activation

La fonction d’activation (ou fonction de seuillage, ou encore fonction de transfert) sert à introduire une non-linéarité dans le fonctionnement du neurone.

Les fonctions de seuillage présentent généralement trois intervalles :

1. en dessous du seuil, le neurone est non-actif (souvent dans ce cas, sa sortie vaut 0 ou -1) ;
2. aux alentours du seuil, une phase de transition ;
3. au-dessus du seuil, le neurone est actif (souvent dans ce cas, sa sortie vaut 1).

Des exemples classiques de fonctions d’activation sont :

1. La fonction sigmoïde.
2. La fonction tangente hyperbolique.
3. La fonction de Heaviside.

La logique bayésienne, dont le théorème de Cox-Jaynes formalise les questions d’apprentissage, fait intervenir aussi une fonction en S qui revient de façon récurrente :

Propagation de l’information

Ce calcul effectué, le neurone propage son nouvel état interne sur son axone. Dans un modèle simple, la fonction neuronale est simplement une fonction de seuillage : elle vaut 1 si la somme pondérée dépasse un certain seuil ; 0 sinon. Dans un modèle plus riche, le neurone fonctionne avec des nombres réels (souvent compris dans l’intervalle [0,1] ou [-1,1]). On dit que le réseau de neurones passe d'un état à un autre lorsque tous ses neurones recalculent en parallèle leur état interne, en fonction de leurs entrées.

Apprentissage

Base théorique

La notion d’apprentissage, bien que connue déjà depuis Sumer, n’est pas modélisable dans le cadre de la logique déductive : celle-ci en effet procède à partir de connaissances déjà établies dont on tire des connaissances dérivées. Or il s’agit ici de la démarche inverse : par observations limitées, tirer des généralisations plausibles : c'est un procédé par induction.

La notion d’apprentissage recouvre deux réalités souvent traitées de façon successive :

• mémorisation : le fait d’assimiler sous une forme dense des exemples éventuellement nombreux,
• généralisation : le fait d’être capable, grâce aux exemples appris, de traiter des exemples distincts, encore non rencontrés, mais similaires.

Dans le cas des systèmes d’apprentissage statistique, utilisés pour optimiser les modèles statistiques classiques, réseaux de neurones et automates markoviens, c’est la généralisation qui est l’objet de toute l’attention.

Cette notion de généralisation est traitée de façon plus ou moins complète par plusieurs approches théoriques.

• La généralisation est traitée de façon globale et générique par la théorie de la régularisation statistique introduite par Vladimir Vapnik. Cette théorie, développée à l’origine en Union Soviétique, s’est diffusée en Occident depuis la Chute du Mur. La théorie de la régularisation statistique s’est diffusée très largement parmi ceux qui étudient les réseaux de neurones en raison de la forme générique des courbes d’erreurs résiduelles d’apprentissage et de généralisation issues des procédures d’apprentissage itératives telles que les descentes de gradient utilisées pour l’optimisation des perceptrons multi-couches. Ces formes génériques correspondent aux formes prévues par la théorie de la régularisation statistiques ; cela vient du fait que les procédures d’apprentissage par descentes de gradient, partant d’une configuration initiale des poids synaptiques explorent progressivement l’espace des poids synaptiques possibles ; on retrouve alors la problématique de l’augmentation progressive de la capacité d’apprentissage, concept fondamental au cœur de la théorie de la régularisation statistique.
• La généralisation est aussi au cœur de l’approche de l'inférence bayésienne, enseignée depuis plus longtemps. Le théorème de Cox-Jaynes fournit ainsi une base importante à un tel apprentissage, en nous apprenant que toute méthode d’apprentissage est soit isomorphe aux probabilités munies de la relation de Bayes, soit incohérente. C’est là un résultat extrêmement fort, et c’est pourquoi les méthodes bayésiennes sont largement utilisées dans le domaine.

Classe de problèmes solubles

En fonction de la structure du réseau, différents types de fonction sont approchables grâce aux réseaux de neurones :

Fonctions représentables par un perceptron

Un perceptron (un réseau à une unité) peut représenter les fonctions booléennes suivantes : AND, OR, NAND, NOR mais pas le XOR. Comme toute fonction booléenne est représentable à l'aide de AND, OR, NAND et NOR, un réseau de perceptrons est capable de représenter toutes les fonctions booléennes.

Fonctions représentables par des réseaux de neurones multicouches acycliques

• Fonctions booléennes : Toutes les fonctions booléennes sont représentables par un réseau à deux couches. Au pire des cas, le nombre de neurones de la couche cachée augmente de manière exponentielle en fonction du nombre d'entrées.

• Fonctions continues : Toutes les fonctions continues bornées sont représentables, avec une précision arbitraire, par un réseau à deux couches (Cybenko, 1989). Ce théorème s'applique au réseau dont les neurones utilisent la sigmoïde dans la couche cachée et des neurones linéaires (sans seuil) dans la couche de sortie. Le nombre de neurones dans la couche cachée dépend de la fonction à approximer.

• Fonctions arbitraires: N'importe quelle fonction peut être approximée avec une précision arbitraire grâce à un réseau à 3 couches (Théorème de Cybenko, 1988).

Algorithme

La large majorité des réseaux de neurones possède un algorithme « d’entraînement » qui consiste à modifier les poids synaptiques en fonction d’un jeu de données présentées en entrée du réseau. Le but de cet entraînement est de permettre au réseau de neurones « d’apprendre » à partir des exemples. Si l’entraînement est correctement réalisé, le réseau est capable de fournir des réponses en sortie très proches des valeurs d’origines du jeu de données d’entraînement.

Mais tout l’intérêt des réseaux de neurones réside dans leur capacité à généraliser à partir du jeu de test.

On peut donc utiliser un réseau de neurones pour réaliser une mémoire ; on parle alors de mémoire neuronale.

La vision topologique d’un apprentissage correspond à la détermination de l’hypersurface sur où est l’ensemble des réels, et n le nombre d’entrées du réseau.

Apprentissage

Mode supervisé ou non

Un apprentissage est dit supervisé lorsque l’on force le réseau à converger vers un état final précis, en même temps qu’on lui présente un motif.

À l’inverse, lors d’un apprentissage non-supervisé, le réseau est laissé libre de converger vers n’importe quel état final lorsqu’on lui présente un motif.

Surapprentissage

Il arrive souvent que les exemples de la base d'apprentissage comportent des valeurs approximatives ou bruitées. Si on oblige le réseau à répondre de façon quasi parfaite relativement à ces exemples, on peut obtenir un réseau qui est biaisé par des valeurs erronées. Par exemple, imaginons qu'on présente au réseau des couples (xi,f(xi)) situés sur une droite d'équation y=ax+b, mais bruités de sorte que les points ne soient pas exactement sur la droite. S'il y a un bon apprentissage, le réseau répond ax+b pour toute valeur de x présentée. S'il y a surapprentissage, le réseau répond un peu plus que ax+b ou un peu moins, car chaque couple (xi, f(xi) positionné en dehors de la droite va influencer la décision. Pour éviter le surapprentissage, il existe une méthode simple : il suffit de partager la base d'exemples en 2 sous-ensembles. Le premier sert à l'apprentissage et le 2^e sert à l'évaluation de l'apprentissage. Tant que l'erreur obtenue sur le 2^e ensemble diminue, on peut continuer l'apprentissage, sinon on arrête.

Rétropropagation

La rétropropagation consiste à rétropropager l'erreur commise par un neurone à ses synapses et aux neurones qui y sont reliés. Pour les réseaux de neurones, on utilise habituellement la rétropropagation du gradient de l'erreur, qui consiste à corriger les erreurs selon l'importance des éléments qui ont justement participé à la réalisation de ces erreurs : les poids synaptiques qui contribuent à engendrer une erreur importante se verront modifiés de manière plus significative que les poids qui ont engendré une erreur marginale.

Élagage

L'élagage ("pruning", en anglais) est une méthode qui permet d'éviter le surapprentissage tout en limitant la complexité du modèle. Elle consiste à supprimer des connexions (ou synapses), des entrées ou des neurones du réseau une fois l'apprentissage terminé. En pratique, les éléments qui ont la plus petite influence sur l'erreur de sortie du réseau sont supprimés. Les deux algorithmes d'élagage les plus utilisés sont :

• Optimal Brain Damage (OBD) de Y. LeCun et al.
• Optimal Brain Surgeon (OBS) de B. Hassibi et D.G. Stork

Différents types de réseaux de neurones

L’ensemble des poids des liaisons synaptiques détermine le fonctionnement du réseau de neurones. Les motifs sont présentés à un sous-ensemble du réseau de neurones : la couche d’entrée. Lorsqu’on applique un motif à un réseau, celui-ci cherche à atteindre un état stable. Lorsqu’il est atteint, les valeurs d’activation des neurones de sortie constituent le résultat. Les neurones qui ne font ni partie de la couche d’entrée ni de la couche de sortie sont dits neurones cachés.

Les types de réseau de neurones diffèrent par plusieurs paramètres :

• la topologie des connexions entre les neurones ;
• la fonction d’agrégation utilisée (somme pondérée, distance pseudo-euclidienne...) ;
• la fonction de seuillage utilisée (sigmoïde, échelon, fonction linéaire, fonction de Gauss, ...) ;
• l’algorithme d’apprentissage (rétropropagation du gradient, cascade correlation) ;
• d’autres paramètres, spécifiques à certains types de réseaux de neurones, tels que la méthode de relaxation pour les réseaux de neurones (e.g. réseaux de Hopfield) qui ne sont pas à propagation simple (e.g. Perceptron Multicouche).

De nombreux autres paramètres sont susceptibles d’être mis en œuvre dans le cadre de l’apprentissage de ces réseaux de neurones par exemple :

• la méthode de dégradation des pondérations (weight decay), permettant d’éviter les effets de bord et de neutraliser le sur-apprentissage.

Réseaux à apprentissages supervisés

Sans rétropropagation

Perceptron

ADALINE (ADAptive LInear NEuron)

Le réseau ADALINE est proche du modèle Perceptron, seule sa fonction d'activation est différente puisqu'il utilise une fonction linéaire. Afin de réduire les parasites reçus en entrée, les réseaux ADALINE utilisent la méthode des moindres carrés.

Le réseau réalise une somme pondérées de ses valeurs d'entrées et y rajoute une valeur de seuil prédéfinie. La fonction de transfert linéaire est ensuite utilisée pour l'activation du neurone. Lors de l'apprentissage, les coefficients synaptiques des différentes entrées sont modifiées en utilisant la loi de Widrow-Hoff (en). Ces réseaux sont souvent employés en traitement de signaux^[4], notamment pour la réduction de bruit.

Machine de Cauchy

Non détaillés

1. Adaptive Heuristic Critic (AHC)
2. Time Delay Neural Network (TDNN)
3. Associative Reward Penalty (ARP)
4. Avalanche Matched Filter (AMF)
5. Backpercolation (Perc)
6. Artmap
7. Adaptive Logic Network (ALN)
8. Cascade Correlation (CasCor)
9. Extended Kalman Filter(EKF)
10. Learning Vector Quantization (LVQ)
11. Probabilistic Neural Network (PNN)
12. General Regression Neural Network (GRNN)

Avec rétropropagation

Perceptron multicouche

Non détaillés

1. Brain-State-in-a-Box (BSB)
2. Fuzzy Cognitive Map (FCM)
3. Boltzmann Machine (BM)
4. Mean Field Annealing (MFT)
5. Recurrent Cascade Correlation (RCC)
6. Backpropagation through time (BPTT)
7. Real-time recurrent learning (RTRL)
8. Recurrent Extended Kalman Filter (EKF)

Réseaux à apprentissage non supervisé

Avec rétropropagation

Carte auto adaptative

Non détaillés

1. Additive Grossberg (AG)
2. Shunting Grossberg (SG)
3. Binary Adaptive Resonance Theory (ART1)
4. Analog Adaptive Resonance Theory (ART2, ART2a)
5. Discrete Hopfield (DH)
6. Continuous Hopfield (CH)
7. Chaos Fractal^[5],[6],[7]
8. Discrete Bidirectional Associative Memory (BAM)
9. Temporal Associative Memory (TAM)
10. Adaptive Bidirectional Associative Memory (ABAM)
11. Apprentissage compétitif

Dans ce type d'apprentissage non supervisé, les neurones sont en compétition pour être actifs. Ils sont à sortie binaire et on dit qu'ils sont actifs lorsque leur sortie vaut 1. Alors que dans les autres règles plusieurs sorties de neurones peuvent être actives simultanément, dans le cas de l'apprentissage compétitif, un seul neurone est actif à un instant donné. Chaque neurone de sortie est spécialisé pour « détecter » une suite de formes similaires et devient alors un détecteur de caractéristiques. La fonction d’entrée est dans ce cas, h = b-dist(W, X) où b, W et X sont respectivement les vecteurs seuil, poids synaptiques et entrées. Le neurone gagnant est celui pour lequel h est maximum donc si les seuils sont identiques, celui dont les poids sont les plus proches des entrées. Le neurone dont la sortie est maximale sera le vainqueur et sa sortie sera mise à 1 alors que les perdants auront leur sortie mise à 0. Un neurone apprend en déplaçant ses poids vers les valeurs des entrées qui l'activent pour augmenter ses chances de gagner. Si un neurone ne répond pas à une entrée, aucun ajustement de poids n'intervient. Si un neurone gagne, une portion des poids de toutes les entrées est redistribuée vers les poids des entrées actives. L'application de la règle donne les résultats suivants (Grossberg) : Dwij = lr(xj-wij) si le neurone i gagne, Dwij = 0 si le neurone i perd. Cette règle a pour effet de rapprocher le vecteur poids synaptique wij de la forme d'entrée xj.

Exemple : Considérons deux nuages de points du plan que l’on désire séparer en deux classes. x1 et x2 sont les deux entrées, w11 et w12 sont les poids du neurone 1 que l’on peut considérer comme les coordonnées d’un point ‘poids du neurone 1’ et w21 et w22 sont les poids du neurone 2. Si les seuils sont nuls, hi sera la distance entre les points à classer et les points poids. La règle précédente tend à diminuer cette distance avec le point échantillon lorsque le neurone gagne. Elle doit donc permettre à chaque point poids de se positionner au milieu d’un nuage. Si on fixe initialement les poids de manière aléatoire, il se peut que l’un des neurones se positionne près des deux nuages et que l’autre se positionne loin de sorte qu’il ne gagne jamais. Ses poids ne pourront jamais évoluer alors que ceux de l’autre neurone vont le positionner au milieu des deux nuages. Le problème de ces neurones que l’on qualifie de morts peut être résolu en jouant sur les seuils. En effet, il suffit d’augmenter le seuil de ces neurones pour qu’ils commencent à gagner.

Applications : Ce type de réseau et la méthode d'apprentissage correspondant peuvent être utilisés en analyse de données afin de mettre en évidence des similitudes entre certaines données.

Précisions

S’agissant d’un modèle, les réseaux de neurones sont généralement utilisés dans le cadre de simulation logicielle. IMSL et Matlab disposent ainsi de bibliothèques dédiées aux réseaux de neurones. Cependant, il existe quelques implémentations matérielles des modèles les plus simples, comme la puce ZISC.

Voir aussi

• Sciences cognitives
• Intelligence artificielle
• Connexionnisme
• Neurone formel
• Statistiques
• Réseaux bayésiens
• Algorithme émergent
• Analyse multivariée
• Arbre de décision
• Self Organising Map
• Réseau de neurones de Hopfield

Références

• Warren Sturgis McCulloch and Walter Pitts. A logical calculus of the ideas immanent in nervous activity. Bulletin of Mathematical Biophysics, 5:115-133, 1943.
• Franck Rosenblatt. The Perceptron : probabilistic model for information storage and organization in the brain. Psychological Review, 65:386-408, 1958.
• Marvin Lee Minsky and Seymour Papert. Perceptrons : an introduction to computational geometry. MIT Press, expanded edition, 1988.
• John Joseph Hopfield. Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Sciences, 79:2554-2558, 1982.
• Y. Le Cun. Une procédure d’apprentissage pour réseau à seuil asymétrique. COGNITIVA 85, Paris, 4-7 juin 1985.
• D. E. Rumelhart and J. L. Mc Clelland. Parallel Distributed Processing: Exploration in the MicroStructure of Cognition. MIT Press, Cambridge, 1986.
• J. A. Anderson and E. Rosenfeld. Neuro Computing Foundations of Research. MIT Press, Cambridge, 1988.
• Tom Mitchell. Machine Learning. McGraw-Hill Science, 1997.

Notes et références

Bibliographie

• François Blayo et Michel Verleysen, "Les réseaux de neurones artificiels", Presses Universitaires de France, Que Sais-je No 3042, 1ère édition, 1996
• Léon Personnaz et Isabelle Rivals, Réseaux de neurones formels pour la modélisation, la commande et la classification, CNRS Editions, 2003.
• Richard P. Lippman, An Introduction to Computing with Neural Nets, IEEE ASSP Magazine, avril 1987, p. 4-22
• Neural Networks : biological computers or electronic brains - Les entretiens de Lyon – (sous la direction de École normale supérieure de Lyon) - Editions Springer-Verlag 1990.
• Jean-Paul Haton, Modèles connexionnistes pour l’intelligence artificielle, 1989.
• Gérard Dreyfus, Jean-Marc Martinez, Mannuel Samuelides, Mirta Gordon, Fouad Badran, Sylvie Thiria, "Apprentissage statistique : réseaux de neurones, cartes topologiques, machines à vecteurs supports" Eyrolles [2008].
• Simon Haykin, « Neural Networks : A Comprehensive Foundation (2nd Edition) », [1998] Prentice Hall.
• Christopher M. Bishop, « Neural Networks for Pattern Recognition », Oxford University Press [1995].
• Christopher M. Bishop, Pattern Recognition And Machine Learning, Springer, 2006 (ISBN 0-387-31073-8)  [détail des éditions]
• Richard O. Duda, Peter E. Hart, David G. Stork, Pattern classification, Wiley-interscience, 2001 (ISBN 0-471-05669-3)  [détail des éditions]
• Ben Krose et Patrick van der Smagt, «  An Introduction to Neural Networks » [8ème édition, 1996]
• Claude Touzet, Les réseaux de neurones : Introduction connexionnisme, EC2, 1992, 160 p. , téléchargement PDF
• Marc Parizeau, Réseaux de Neurones (Le perceptron multicouche et son algorithme de retropropagation des erreurs), Université Laval, Laval, 2004, 272 p.
• Fabien Tschirhart (dir. Alain Lioret), Réseaux de neurones formels appliqués à l'Intelligence Artificielle et au jeu, ESGI _{(mémoire de master de recherche en multimédia et animation numérique)}, Paris, 2009, 121 p. [mémoire en ligne (page consultée le 8 novembre 2010)]

• Portail des probabilités et des statistiques
• Portail de l'informatique théorique