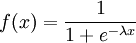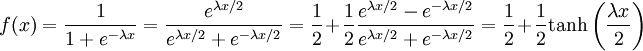Sigmoide (mathematiques)

Sigmoide (mathematiques)

Sigmoïde (mathématiques)

La fonction sigmoïde

En mathématiques, la fonction sigmoïde (dite aussi courbe en S) est définie par :

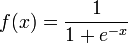f(x)=\frac{1}{1 + e^{- x}} pour tout réel x\,

mais on la généralise à toute fonction dont l'expression est :

f(x)=\frac{1}{1 + e^{-\lambda x}}

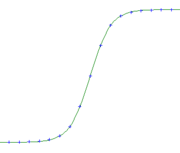
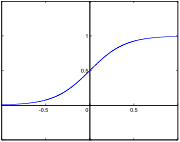
Le nom de « sigmoïde » lui vient de sa forme en S.

Elle est souvent utilisée dans les réseaux de neurones et représente la fonction de répartition de la loi logistique. En particulier, cette fonction est utilisée dans la rétroprogation de l'algorithme de Werbos, concernant le seuil d'activation des neurones (assez efficace en simulation des réseaux neuronaux-simulés, quant aux caractéristiques de la vision, et de la reconnaisance des formes).

Une courbe sigmoïde génère par transformation affine une partie des courbes logistiques et en est donc un représentant privilégié.

Propriétés graphiques

La courbe sigmoïde possède pour asymptotes les droites d'équation y = 0 et y = 1. Elle a pour centre de symétrie le point I (0;1/2) qui en est un point d'inflexion. En ce point, la dérivée seconde est nulle.

La fonction sigmoïde avec λ = 5.

Pour une courbe sigmoïde de paramètre λ la tangente au point d'inflexion est λ/4. Cette propriété permet de paramétrer facilement une sigmoïde en observant la pente au point d'inflexion.

Équation différentielle

Les propriétés de la fonction sigmoïde s'expliquent par celles de sa dérivée. En effet celle-ci est égale à

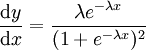\frac{\mathrm dy}{\mathrm dx} = \frac{\lambda e^{-\lambda x}}{(1 + e^{-\lambda x})^2},

qui peut se transformer en

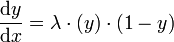\frac{\mathrm dy}{\mathrm dx} = \lambda \cdot ( y ) \cdot (1-y). y varie de 0 à +1.

Cette équation différentielle signifie que la variation de y en fonction de x (souvent le temps d'ailleurs en physique, chimie ou marketing) est proportionnelle à la fois à l'avancement de y depuis 0 et au chemin qui reste à parcourir pour arriver à 1, proportionnalité affectée d'un coefficient λ.

Cette équation différentielle est un cas particulier de modèle de Verhulst et a pour autres solutions des fonctions logistiques.

La dérivée seconde possède aussi quelques propriétés : elle peut se transformer en

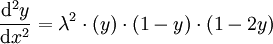\frac{\mathrm d^2y}{\mathrm dx^2} = \lambda^2 \cdot ( y ) \cdot (1-y) \cdot (1-2y).

ce qui vérifie bien qu'un point d'inflexion est le point-milieu y=½. Les autres points d'inflexion sont rencontrés aux extrémités de la courbe (y=0 et y=1), il s'agit plutôt de points asymptotiques de rayon infini.

Ecriture alternative

La fonction sigmoïde peut s'exprimer à l'aide de la fonction tangente hyperbolique dont la courbe représentative a aussi une forme en S mais dont les asympotes ont pour équation y = -1 et y = 1

f(x) = \frac{1}{1+e^{-\lambda x}} = \frac{e^{\lambda x/2}}{e^{\lambda x/2}+e^{-\lambda x/2}}= \frac 12 +\frac 12 \frac{e^{\lambda x/2}- e^{-\lambda x/2}}{e^{\lambda x/2}+e^{-\lambda x/2}} = \frac 12 +\frac 12 \operatorname{tanh}\left(\frac{\lambda x}2\right)
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Sigmo%C3%AFde (math%C3%A9matiques) ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Sigmoide (mathematiques) de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Sigmoïde (mathématiques) — Pour les articles homonymes, voir Sigmoïde. La fonction sigmoïde En mathématiques, la fonction sigmoïde (dite aussi courbe en S) est définie par  …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Courbe logistique — Fonction logistique (Verhulst) Fonction logistique, cas particulier: sigmoïde. En mathématiques les fonctions logistiques sont les fonctions ayant pour expression où K et r sont des réels positifs et a un réel quelconque …   Wikipédia en Français

  • Fonction Logistique (Verhulst) — Fonction logistique, cas particulier: sigmoïde. En mathématiques les fonctions logistiques sont les fonctions ayant pour expression où K et r sont des réels positifs et a un réel quelconque …   Wikipédia en Français

  • Fonction logistique (verhulst) — Fonction logistique, cas particulier: sigmoïde. En mathématiques les fonctions logistiques sont les fonctions ayant pour expression où K et r sont des réels positifs et a un réel quelconque …   Wikipédia en Français

  • Fonction logistique (Verhulst) — Fonction logistique, cas particulier: sigmoïde. En mathématiques, les fonctions logistiques sont les fonctions ayant pour expression où K et r sont des réels positifs et …   Wikipédia en Français

  • Neurone Formel — Un neurone formel est une représentation mathématique et informatique d un neurone biologique. Le neurone formel possède généralement plusieurs entrées et une sortie qui correspondent respectivement aux dendrites et au cône d émergence du neurone …   Wikipédia en Français

  • Neurone formel — Représentation d un neurone formel (ou logique) Un neurone formel est une représentation mathématique et informatique d un neurone biologique. Le neurone formel possède généralement plusieurs entrées et une sortie qui correspondent respectivement …   Wikipédia en Français

  • CROISSANCE (biologie) — La notion de croissance s’est imposée d’abord à l’esprit humain par l’observation de l’augmentation de taille des êtres vivants. Puis l’emploi du mot s’est élargi, soit par application à divers produits de leurs activités ou par métaphore (la… …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”