Gradient conjugué

Gradient conjugué

Méthode du gradient conjugué

En analyse numérique, la méthode du gradient conjugué est un algorithme pour résoudre des systèmes d'équations linéaires dont la matrice est symétrique et définie positive. Cette méthode est une méthode itérative.

La méthode du gradient biconjugué fournit une généralisation pour les matrices non symétriques.

Principe

L'objectif est de minimiser la fonction 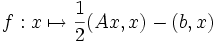f: x \mapsto \frac{1}{2} (Ax,x) -(b,x) où A est une matrice carrée symétrique définie positive de taille n.

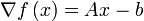Le calcul montre qu'une solution du problème est la solution du système Ax = b : en effet , on a \nabla f \left ( x \right) = Ax-b .

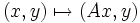La méthode du gradient conjugué consiste donc à construire par récurrence une base de vecteurs de \mathbb{R}^n orthogonaux pour le produit scalaire \left (x , y \right ) \mapsto (Ax,y) , et exprimer le vecteur solution dans cette base.

Implémentation

Un exemple d'implémentation pour Octave:

 function [x] = conjgrad(A,b,x0)
  
 r = b - A*x0;
 w = -r;
 z = A*w;
 a = (r'*w)/(w'*z);
 x = x0 + a*w;
 B = 0;
  
 for i = 1:size(A)(1);
    r = r - a*z;
    if( r < 1e-10 )
         break;
    endif
    B = (r'*z)/(w'*z);
    w = -r + B*w;
    z = A*w;
    a = (r'*w)/(w'*z);
    x = x + a*w;
 end

Liens

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « M%C3%A9thode du gradient conjugu%C3%A9 ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Gradient conjugué de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Methode du gradient conjugue — Méthode du gradient conjugué En analyse numérique, la méthode du gradient conjugué est un algorithme pour résoudre des systèmes d équations linéaires dont la matrice est symétrique et définie positive. Cette méthode est une méthode itérative. La… …   Wikipédia en Français

  • Méthode Du Gradient Conjugué — En analyse numérique, la méthode du gradient conjugué est un algorithme pour résoudre des systèmes d équations linéaires dont la matrice est symétrique et définie positive. Cette méthode est une méthode itérative. La méthode du gradient… …   Wikipédia en Français

  • Méthode du gradient conjugué — En analyse numérique, la méthode du gradient conjugué est un algorithme pour résoudre des systèmes d équations linéaires dont la matrice est définie positive (et par conséquent symétrique). Cette méthode, imaginée en 1950 simultanément par… …   Wikipédia en Français

  • Algorithme du gradient — L algorithme du gradient désigne un algorithme d optimisation différentiable. Il est par conséquent destiné à minimiser une fonction réelle différentiable définie sur un espace euclidien (par exemple, , l espace des n uplets de nombres réels,… …   Wikipédia en Français

  • Méthode du gradient biconjugué — En mathématiques, plus spécifiquement en analyse numérique, la méthode du gradient biconjugué est un algorithme permettant de résoudre un système d équations linéaires Contrairement à la méthode du gradient conjugué, cet algorithme ne nécessite… …   Wikipédia en Français

  • Methode du gradient biconjugue — Méthode du gradient biconjugué En mathématiques, plus spécifiquement en analyse numérique, la méthode du gradient biconjugué est un algorithme permettant de résoudre un système d équations linéaires Contrairement à la méthode du gradient conjugué …   Wikipédia en Français

  • Méthode Du Gradient Biconjugué — En mathématiques, plus spécifiquement en analyse numérique, la méthode du gradient biconjugué est un algorithme permettant de résoudre un système d équations linéaires Contrairement à la méthode du gradient conjugué, cet algorithme ne nécessite… …   Wikipédia en Français

  • Descente De Gradient — Traduction à relire Gradient descent → …   Wikipédia en Français

  • Descente de gradient — Traduction à relire Gradient descent → …   Wikipédia en Français

  • Direction de descente — En optimisation différentiable, qui est une discipline d analyse numérique en mathématiques étudiant en particulier les algorithmes minimisant des fonctions différentiables sur des ensembles, une direction de descente est une direction le long de …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”