Rigueur mathématique

La logique mathématique est née à la fin du XIX^e siècle de la logique au sens philosophique du terme. Ses débuts furent marqués par la rencontre entre deux idées nouvelles :

• la volonté chez Frege, Russell, Peano et Hilbert de donner une fondation axiomatique aux mathématiques ;
• la découverte par George Boole de l'existence de structures algébriques permettant de définir un « calcul de vérité ».

La logique mathématique a repris l'objectif de la logique, d'étudier le raisonnement, mais en se restreignant au langage des mathématiques qui présente l'avantage d'être extrêmement normalisé.

Avant de trouver son nom actuel, attribué à Giuseppe Peano, elle s'est appelée « logique symbolique » (en opposition à la logique philosophique) et « métamathématique » (terminologie de Hilbert).

Au cours du XX^e siècle, la logique mathématique s'est ramifiée en de nombreux sous-domaines :

• la théorie des ensembles ;
• la théorie de la démonstration ;
• la théorie des modèles ;
• la théorie de la calculabilité.

Cette classification en quatre grands axes, généralement admise, est celle proposée par Jon Barwise éditeur de l'ouvrage collectif Handbook of Mathematical Logic. Depuis, un cinquième grand axe semble se dessiner avec les travaux sur la théorie des types.

Sommaire 1 Quelques données d'histoire 2 Quelques résultats fondamentaux 3 Système logique 3.1 Définition 3.2 Syntaxe et sémantique 3.3 Systèmes de déduction 4 Le calcul des propositions 4.1 Connecteurs les plus fréquents 4.2 En logique classique un unique connecteur suffit 5 Le calcul des prédicats 5.1 Substitution 5.2 Les quantificateurs 5.3 Utilisation des quantificateurs 6 Quelques systèmes déductifs 7 La théorie des ensembles 7.1 L’égalité 7.2 L’appartenance 8 Notes et références 9 Bibliographie 10 Voir aussi

Quelques données d'histoire

Les premières tentatives de traitement formel des mathématiques sont dues à Leibniz et Lambert ; Leibniz a en particulier introduit une grande partie de la notation mathématique moderne (usage des quantificateurs, symbole d'intégration, etc.). Toutefois on ne peut parler de logique mathématique qu'à partir du milieu du XIXe siècle avec les travaux de George Boole (et dans une moindre mesure ceux d'Auguste De Morgan) qui introduit un calcul de vérité où les combinaisons logiques comme la conjonction, la disjonction et l'implication, sont des opérations analogues à l'addition ou la multiplication des entiers, mais portant sur les valeurs de vérité faux et vrai (ou 0 et 1) ; ces opérations booléennes se définissent au moyen de tables de vérité.

Le calcul de Boole semblait une piste fructueuse afin de résoudre les problèmes de fondation des mathématiques dus à leur complexification et à l'apparition des paradoxes, mais il ne permettait pas de prendre en compte la notion de variable. Dès lors, nombre de mathématiciens ont cherché à l'étendre au cadre général du raisonnement mathématique et on a vu apparaître les systèmes logiques formalisés ; l'un des premiers est dû à Frege au tournant du XX^e siècle.

En 1900 au cours d'une très célèbre conférence au congrès international de mathématiques à Paris, David Hilbert a proposé une liste des 23 problèmes non résolus les plus importants des mathématiques d'alors. Le deuxième était celui de la cohérence de l'arithmétique, c’est-à-dire de démontrer par des moyens finitistes la non-contradiction des axiomes de l'arithmétique.

Le programme de Hilbert a suscité de nombreux travaux en logique dans le premier quart du siècle, notamment le développement de systèmes d'axiomes pour les mathématiques : les axiomes de Peano pour l'arithmétique, ceux de Zermelo complété par Skolem et Fraenkel pour la théorie des ensembles et le développement par Whitehead et Russell d'un programme de formalisation des mathématiques, les Principia Mathematica. C'est également la période où apparaissent les principes fondateurs de la théorie des modèles : notion de modèle d'une théorie, théorème de Löwenheim-Skolem.

En 1929 Kurt Gödel montre dans sa thèse de doctorat son théorème de complétude qui énonce le succès de l'entreprise de formalisation des mathématiques : tout raisonnement mathématique peut en principe être formalisé dans le calcul des prédicats. Ce théorème a été accueilli comme une avancée notable vers la résolution du programme de Hilbert, mais un an plus tard, Gödel démontrait le théorème d'incomplétude (publié en 1931) qui montrait irréfutablement l'impossibilité de réaliser ce programme.

Ce résultat négatif n'a toutefois pas arrêté l'essor de la logique mathématique. Les années 30 ont vu arriver une nouvelle génération de logiciens anglais et américains, notamment Alonzo Church, Alan Turing, Stephen Kleene, Haskell Curry et Emil Post, qui ont grandement contribué à la définition de la notion d'algorithme et au développement de la théorie de la complexité algorithmique (théorie de la calculabilité, théorie de la complexité). La théorie de la démonstration de Hilbert a également continué à se développer avec les travaux de Gerhard Gentzen qui a produit la première démonstration de cohérence relative et initié ainsi un programme de classification des théories axiomatiques.

Le résultat le plus spectaculaire de l'après-guerre est dû à Paul Cohen qui démontre en utilisant la méthode du forcing l'indépendance de l'hypothèse du continu en théorie des ensembles, résolvant ainsi le 1^er problème de Hilbert. Mais la logique mathématique subit également une révolution due à l'apparition de l'informatique ; la découverte de la correspondance de Curry-Howard qui relie les preuves formelles au lambda-calcul de Church et donne un contenu calculatoire aux démonstrations va déclencher un vaste programme de recherche.

Quelques résultats fondamentaux

Quelques résultats importants ont été établis pendant la décennie 1930 :

• Le théorème de complétude du calcul des prédicats du premier ordre que Gödel a montré dans sa thèse de doctorat, un an avant son célèbre théorème d'incomplétude. Ce théorème énonce que toute démonstration mathématique peut être représentée dans le formalisme du calcul des prédicats (qui est donc complet).

• L'ensemble des théorèmes du calcul des prédicats n'est pas calculable, c'est-à-dire qu'aucun algorithme ne permet de vérifier si un énoncé donné est prouvable ou non. Il existe, cependant, un semi-algorithme : celui-ci prend en entrée une formule du premier ordre ; il s'interrompt en répondant «oui» si la formule est universellement valide, et continue indéfiniment sinon. Même si ce semi-algorithme s'exécute pendant des milliards d'années, il peut ne pas conclure qu'une proposition n'est pas universellement valide. En d'autres termes, l'ensemble des formules du premier ordre universellement valide est « récursivement énumérable » ; on dit qu'il est « semi-décidable ».

• La cohérence (non contradiction) d'un système d'axiomes (par exemple : les axiomes de Peano pour l'arithmétique) n'est pas une conséquence de ces seuls axiomes sauf dans des cas triviaux (notamment lorsque les axiomes sont contradictoires entre eux). C'est le fameux second théorème d'incomplétude de Gödel.

• L'ensemble de toutes les formules universellement valides du second ordre n'est pas énumérable, même récursivement. Ceci est une conséquence du théorème d'incomplétude.

• Tout théorème purement logique peut être démontré en n'utilisant à tout moment que des propositions qui sont des sous-formules de son énoncé. Connu sous le nom de théorème de la sous-formule, il est une conséquence du théorème d'élimination des coupures en calcul des séquents de Gerhard Gentzen.
  • Accessoirement, ce théorème de la sous-formule fournit un théorème de cohérence pour la logique, car il interdit la dérivation de la formule vide (identifiée à l'absurdité).

D'autres résultats importants ont été établis pendant la deuxième partie du XX^e siècle.

• L'indépendance de l'hypothèse du continu par rapport aux autres axiomes de la théorie des ensembles (ZF) est achevée en 1963 par Paul Cohen^[1].
• La théorie de la calculabilité se développe.
• Au tournant de la décennie 1980, la correspondance de Curry-Howard identifie la simplification des démonstrations et les programmes, créant ainsi un pont entre mathématiques et informatique.
• En 1990, cette correspondance est étendue à la logique classique.

Système logique

Définition

Un système logique ou système de déduction est constitué de trois composantes. Les deux premières définissent sa syntaxe, la troisième sa sémantique :

• Un ensemble de formules, ou faits ; dans les systèmes de logique classique ou intuitionniste, les formules représentent des énoncés mathématiques exprimés formellement. Les formules sont définies par des moyens combinatoires : suites de symboles, arbres étiquetés, graphes...

• Un ensemble de déductions ; les déductions sont également définies par des moyens combinatoires. Une déduction permet de dériver des formules (les formules prouvables ou théorèmes) à partir de formules de départ (les axiomes) au moyen de règles (les règles d'inférence).

• Une interprétation des formules ; il s'agit d'une fonction associant à toute formule un objet dans une structure abstraite appelée modèle, ce qui permet de définir la validité des formules.

Syntaxe et sémantique

La caractéristique principale des formules et des déductions est qu'il s'agit d'objets finis ; plus encore, chacun des ensembles de formules et de déductions est récursif, c'est-à-dire que l'on dispose d'un algorithme qui détermine si un objet donné est une formule correcte ou une déduction correcte du système.

La sémantique, au contraire, échappe à la combinatoire en faisant appel (en général) à des objets infinis. Elle a d'abord servi à « définir » la vérité. Par exemple, en calcul des propositions, les formules sont interprétées par des éléments d'une algèbre de Boole ; les formules valides sont celles qui sont interprétées par le plus grand élément.

Une mise en garde est de rigueur ici, car Kurt Gödel (suivi par Alfred Tarski) a montré avec son théorème d'incomplétude l'impossibilité de définir mathématiquement la vérité mathématique. C'est pourquoi il est plus approprié de voir la sémantique comme une métaphore : les formules — objets syntaxiques — sont projetées dans un autre monde, plus abstrait, par exemple les algèbres de Boole. Cette technique — plonger les objets dans un monde plus vaste pour mieux raisonner dessus — est couramment utilisée en mathématique et a amplement démontré son efficacité.

Ainsi la sémantique ne sert pas qu'à « définir » la vérité. Par exemple, la sémantique dénotationnelle est une interprétation, non des formules, mais des déductions visant à capturer leur contenu calculatoire.

Systèmes de déduction

En logiques classique et intuitionniste, on distingue deux types d'axiomes : les axiomes logiques qui expriment des propriétés purement logiques comme par exemple 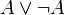(principe du tiers exclu, valide en logique classique mais pas en logique intuitionniste) et les axiomes extra-logiques qui définissent des objets mathématiques, par exemple les axiomes de Peano qui définissent l'arithmétique ou les axiomes de Zermelo-Fraenkel qui définissent la théorie des ensembles. Quand le système possède des axiomes extra-logiques, on parle de théorie axiomatique. L'étude des différents modèles d'une même théorie axiomatique est l'objet de la théorie des modèles.

Deux systèmes de déduction peuvent être équivalents au sens où ils ont exactement les mêmes théorèmes. On démontre cette équivalence en fournissant des traductions des déductions de l'un dans les déductions de l'autre. Par exemple, il existe (au moins) trois types de systèmes de déduction équivalents pour le calcul des prédicats : les systèmes à la Hilbert, la déduction naturelle et le calcul des séquents. On y ajoute parfois le style de Fitch qui est une variante de la déduction naturelle dans laquelle les démonstrations sont présentées de façon linéaire.

Alors que la théorie des nombres démontre des propriétés des nombres, on notera la principale caractéristique de la logique en tant que théorie mathématique : elle « démontre » des propriétés de systèmes de déduction dans lesquels les objets sont des « théorèmes ». Il y a donc un double niveau dans lequel il ne faut pas se perdre. Pour clarifier les choses, les « théorèmes » énonçant des propriétés des systèmes de déduction sont parfois appelés des « métathéorèmes ». Le système de déduction que l'on étudie est appelé la « théorie » et le système dans lequel on énonce et démontre les métathéorèmes est appelé la « métathéorie ».

Les propriétés fondamentales des systèmes de déduction sont les suivantes.

• La correction : La correction énonce que les théorèmes sont valides dans tous les modèles. Cela signifie que les règles d'inférence sont bien adaptées à ces modèles, autrement dit que le système de déduction est une manière de bien raisonner dans ces modèles.

• La cohérence : Un système de déduction est cohérent (on dit aussi qu'il est consistant par mimétisme avec l'anglais) s'il admet un modèle non trivial, c'est-à-dire un modèle qui a au moins deux éléments. Cela revient à affirmer que dans ce système de déduction, il existe des propositions qui ne sont pas des théorèmes.

• La complétude : Elle se définit par rapport à une famille de modèles. Un système de déduction est complet par rapport à une famille de modèles, si toute proposition qui est valide dans tous les modèles de la famille est un théorème. En bref, un système est complet si tout ce qui est valide est démontrable.

Une autre propriété des systèmes de déduction apparentée à la complétude est la cohérence maximale. Un système de déduction est maximalement cohérent, si l'ajout d'un nouvel axiome qui n'est pas lui-même un théorème rend le système incohérent.

Affirmer « tel système est complet pour telle famille de modèles » est un exemple typique de métathéorème.

Dans ce cadre, la notion intuitive de vérité donne lieu à deux concepts formels : la validité et la démontrabilité. Les trois propriétés de correction, cohérence et complétude précisent comment ces notions peuvent être reliées, espérant qu'ainsi la vérité, quête du logicien, puisse être cernée.

Le calcul des propositions

Les propositions sont des assemblages de symboles et de lettres formés en suivant certaines règles de syntaxe. Les symboles de base du calcul des propositions sont appelés connecteurs, ils servent essentiellement à créer de nouvelles propositions à partir de propositions déjà créées. Dans le calcul des propositions, les propositions de base que l'on appelle aussi les variables propositionnelles n'ont pas de contenu (n'ont pas de signification) a priori. On peut remplacer une variable propositionnelle par «il pleut», mais ce n'est pas le contenu météorologique qui intéresse le logicien, mais la façon dont les propositions de base sont combinées pour construire des raisonnements.

Connecteurs les plus fréquents

Les connecteurs sont présentés avec leur interprétation en logique classique.

La disjonction

La disjonction de deux propositions P et Q est la proposition notée P ∨ Q ou « P ou Q » qui est vraie si l’une au moins des deux propositions est vraie, et fausse si les deux propositions sont fausses.

La négation

La négation d’une proposition P, est la proposition notée ¬P, ou « non P » qui est vraie lorsque P est fausse et fausse lorsque P est vraie.

À partir de ces deux connecteurs, on peut construire d’autres connecteurs ou abréviations utiles :

La conjonction

La conjonction de deux propositions P et Q est la proposition suivante :

¬((¬P) ∨ (¬Q)) c'est-à-dire non ( (non P) ou (non Q) )

Celle-ci est notée P ∧ Q ou « P et Q » et n’est vraie que lorsque P et Q sont vraies et fausse si l’une des deux propositions est fausse.

L'implication

L'implication de Q par P est la proposition (¬P) ∨ Q, notée « P ⇒ Q » ou « P implique Q », et qui est fausse seulement si P est une proposition vraie et Q fausse.

L'équivalence

L'équivalence logique de P et Q est la proposition ( (P ⇒ Q) ∧ ( Q ⇒ P) ) ( ((P implique Q) et (Q implique P) )), notée « P ⇔ Q » ou (P est équivalent à Q), et qui n'est vraie que si les deux propositions P et Q ont même valeur de vérité.

Le ou exclusif

Le ou exclusif ou disjonction exclusive de P et Q est la proposition P ∨∨ Q (parfois aussi notée^[2] P ⊕ Q ou encore ^[3] P | Q) qui correspond à (P ∨ Q) ∧ ¬(P ∧ Q), c'est-à-dire en français: soit P, soit Q (mais pas les deux à la fois). Le ou exclusif de P et Q correspond à P ⇔ ¬Q ou encore à ¬(P ⇔ Q). Cette proposition n'est vraie que si P et Q ont des valeurs de vérités distinctes.

En logique classique un unique connecteur suffit

Une caractéristique du calcul propositionnel dit « classique » est que toutes les propositions envisageables peuvent s'exprimer à partir de deux connecteurs : par exemple ∨ et ¬ (ou et non). Mais d'autres choix sont possibles : ainsi, ⇒ (implication) et ⊥ (faux). On sait aussi que l'on peut aussi n'utiliser qu'un seul connecteur, le symbole de Sheffer « | » (Henry M. Sheffer, 1913), appelé « stroke » par son concepteur et appelé aujourd'hui Nand et noté par les concepteurs de circuits ; on peut aussi n'utiliser que le connecteur Nor (noté 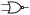) comme l'a remarqué Charles Sanders Peirce (1880) sans le publier.

Le premier article porte sur les aspects de logique mathématique, tandis que le second porte sur les aspects pragmatiques tels qu'ils sont vus par les électroniciens.

Le calcul des prédicats

Substitution

Il est également possible de construire à partir d’une proposition P, d’autres propositions en remplaçant un objet mathématique indéterminé x dans la proposition partout où il intervient, par un autre objet mathématique a.

Par exemple, la proposition P : « 8 est un nombre pair », peut être représentée sous la forme P{8}, où P est le prédicat « est un nombre pair », et 8 est son argument.
Ou par exemple, la proposition « Les droites D et D’ sont parallèles » peut être représentée sous la forme P{D, D’} où P est le prédicat « sont parallèles » et les droites D et D’ sont les arguments.

Si P est une proposition, x un objet indéterminé, et a un objet mathématique, l’assemblage obtenu en remplaçant x par a dans P est encore une proposition notée

(a|x)P

et s’appelle proposition obtenue par substitution de x par a dans P.

Pour mettre en évidence un objet indéterminé x dans une proposition P, on écrit la proposition sous la forme P{x} ; et on note P{a} la proposition (a|x)P.

Soit P une proposition, x un objet indéterminé, et a un objet mathématique donné. Si P est vraie, alors P{a} est vraie.

Et tout cela se généralise au cas de plusieurs objets indéterminés.

Les quantificateurs

Il existe encore un autre procédé logique, permettant de construire d’autres propositions à partir d’une proposition.

Soit une proposition P et x un objet indéterminé. Nous pouvons considérer la proposition :

il existe un objet a, tel que (a|x)P soit vraie

c'est-à-dire

il existe un objet a, tel que P{a} soit vraie

« il existe un objet » signifie intuitivement « nous pouvons trouver au moins un objet ».

Symboliquement, nous écrivons :

∃ a P

ou

∃ a P{a}

ce qui se lit :

« il existe a tel que P »

Ce signe ∃ s’appelle le quantificateur existentiel.

Nous définissons, à partir de ∃ le symbole ∀  :

Soit P une proposition et x un objet indéterminé, la proposition notée ∀ x P est la proposition

¬( ∃x ¬P )

et se lit « pour tout x, P »
ou « quel que soit x, on a P vraie »

∀ s’appelle le quantificateur universel.

Évidemment, la proposition (∀ x P) est fausse si et seulement si (∃ x ¬ P) est vraie.

Utilisation des quantificateurs

Propriétés élémentaires

Soient P et Q deux propositions et x un objet indéterminé.

• ¬(∃ x P) ⇔ (∀ x ¬ P)
• (∀ x) (P∧Q) ⇔ ( (∀ x) P ∧ (∀ x) Q )
• (∀ x) P ∨ (∀ x) Q ⇒ (∀ x) (P ∨ Q )
  (Implication réciproque fausse en général)
• (∃ x) (P∨Q) ⇔ ( (∃ x) P ∨ (∃ x) Q )
• (∃ x) (P∧Q) ⇒ ( (∃ x) P ∧ (∃ x) Q )
  (Implication réciproque fausse en général)

Propriétés utiles

Soient P une proposition et x et y des objets indéterminés.

• (∀ x) (∀ y) P ⇔ (∀ y) (∀ x) P
• (∃ x) (∃ y) P ⇔ (∃ y) (∃ x) P
• (∃ x) (∀ y) P ⇒ (∀ y) (∃ x) P
  (Implication réciproque fausse en général)

La dernière implication dit que s’il existe un x, tel que pour tout y, on ait P vraie, alors pour tout y, il existe bien un x (celui obtenu avant) tel que P soit vraie.

Intuitivement, l’implication réciproque est fausse en général, parce que si pour chaque y, il existe un x tel que P soit vraie, ce x pourrait dépendre de y et varier suivant y. Ce x pourrait donc ne pas être le même pour tout y tel que P soit vraie.

Quelques systèmes déductifs

• Les systèmes à la Hilbert ;
• La déduction naturelle ;
• Le calcul des séquents ;

La théorie des ensembles

La théorie des ensembles est à la base de nombreuses théories mathématiques. Outre les symboles de logique énumérés précédemment, cette théorie utilise des autres symboles = et ∈ permettant de mettre des objets mathématiques en relation. Les objets mathématiques sont appelés des ensembles.

L’égalité

Le signe de l’égalité se note

=

et représente la relation d’égalité entre objets mathématiques.

Nous nous contenterons de la définition intuitive :

Soient a et b deux objets. a = b signifie que a et b représentent des objets identiques, et se lit « a est égal à b »

≠ est définie par a ≠ b si ¬(a = b)

Propriétés :

• (∀ x) (x = x) vraie (réflexivité de =)
• (∀ x) (∀ y) ( (x = y) ⇔ (y = x) ) vraie (symétrie de =)
• (∀ x) (∀ y) (∀ z) ( ((x = y) ∧ (y = z)) ⇒ (x = z) ) (transitivité de =)

La relation = étant réflexive, symétrique et transitive, on dit que la relation = est une relation d'équivalence

• Soit P(x) une propriété contenant une variable libre x. Soient a et b des constantes d'individu telles que a = b. Alors les propositions P(a) et P(b) (obtenues en remplaçant respectivement x par a et x par b dans P(x)) sont équivalentes.

• Soit F(x) une fonction contenant une variable libre x. Soient a et b des constantes d'individu telles que a = b. Alors les propositions F(a) et F(b) (obtenues en remplaçant respectivement x par a et x par b dans F(x)) sont égales.

Ces deux dernières propriétés expriment intuitivement que = est la plus fine des relations d'équivalence.

L’appartenance

Le signe de l’appartenance se note :

∈

et représente la relation d’appartenance d’un objet à un autre.

Si a et b sont deux objets a ∈ b se lit :

« a appartient à b »

ou encore

« a est élément de b »

∉ se définit par a ∉ b si ¬(a ∈ b) vraie.

a ∉ b se lit « a n’appartient pas à b »

Théorème :

Soient a et b deux objets mathématiques.

a = b ⇔ ( (∀x) (x ∈ a ⇔ x ∈ b) )

Pour les règles d'utilisation de ces symboles, reportez-vous à l'article langage formel mathématique.

Notes et références

Bibliographie

• Alonzo Church, Introduction to mathematical logic, Princeton University Press, ISBN 0691029067
• Stephen Kleene, logique mathématique, Armand Colin, 1971 ou Gabay 1987, ISBN 2876470055
• Yannis Delmas-Rigoutsos et René Lalement, La Logique ou l'art de raisonner, 2000 [détail des éditions] 
• R. David, K. Nour et C. Raffalli, Introduction à la logique. Théorie de la démonstration. Cours et exercices corrigés, Dunod, 2001, ISBN 2100067966
• Gilles Dowek, La logique, Coll. Dominos, Flammarion (1995).
• René Cori, Daniel Lascar, Logique mathématique tomes 1 et 2, ISBN 210005452X et ISBN 2100054538
• René Lalement, Logique, réduction, résolution, Masson, 1990

Voir aussi

• logique, logique classique, logique intuitionniste, logique minimale, logique linéaire.
• syllogisme
• idéographie
• lambda-calcul
• Logiques multi-valuées
• Logique de description

• Portail des mathématiques
• Portail de la logique