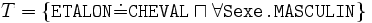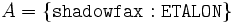Logique De Description

Logique de description

Les logiques de description aussi appelé logiques descriptives (LDs) sont une famille de langages de représentation de connaissance qui peuvent être utilisés pour représenter la connaissance terminologique d'un domaine d'application d'une manière formelle et structurée. Le nom de logique de description se rapporte, d'une part à la description de concepts utilisée pour décrire un domaine et d'autre part à la sémantique basée sur la logique qui peut être donnée par une transcription en logique des prédicats du premier ordre. La logique de description a été développée comme une extension des frames et des réseaux sémantiques, qui ne possédaient pas de sémantique formelle basée sur la logique.

Sommaire

1 Origines et applications des logiques de description
2 Définition des logiques de description
3 Les tâches de raisonnement
4 Références
5 Voir aussi
6 Liens externes

Origines et applications des logiques de description

Les logiques de description ont été conçues à partir des réseaux sémantiques de Quillian (ref) qui sont des graphes orientés étiquetés auxquels on associe des concepts aux nœuds et des relations aux arcs, et de la sémantique des cadres de Minsky (ref) où l'on a des concepts représentés par des cadres qui sont caractérisés par un certain nombre d'attributs (appelés aussi slots) qui contiennent de l'information sur leur contenu.

Les logiques de description forment une famille de langages de représentation de connaissance qui peuvent être utilisées pour représenter la connaissance terminologique d'un domaine d'application d'une façon structurée et formelle. Le nom « logique de description » peut être interprété de deux manières. D'une part ces langages ont été élaborés pour écrire la « description » des concepts pertinents d'un domaine d'application. D'autre part, une caractéristique cruciale de ces langages est qu'ils ont une sémantique formelle définie en logique du premier ordre (à la différence des propositions précédentes comme les cadres de Minsky). Dans ce sens, nous pouvons dire que les LDs ont une sémantique « descriptive » formelle.

Les logiques de description sont utilisées pour de nombreuses applications (voir International Workshop on Description Logics et Workshop on Applications of Description Logics). Sans être exhaustif, nous pouvons dire que ces applications font partie des domaines suivants :

le web sémantique (e.g., représentation d'ontologies, et recherche d'information basée sur la logique)
médecine/bio-informatique (e.g., représenter et gérer des ontologies biomédicales)
traitement automatique des langues et représentation de la connaissance
Ingénierie de processus (e.g., représenter des descriptions de service)
Ingénierie de la connaissance (e.g., représenter des ontologies)
Ingénierie logicielle (e.g., représenter la sémantique des diagrammes de classe UML)

Définition des logiques de description

La plupart des logiques de description divisent la connaissance en deux parties :

les informations terminologiques: définition des notions basiques ou dérivées et de comment elles sont reliées entre elles. Ces informations sont "génériques" ou "globales", vraies dans tous les modèles et pour tous les individus.
les informations sur les individus: ces informations sont "spécifiques" ou "locales", vraies pour certains individus particuliers.

Toutes les informations connues sont alors modélisées comme un couple 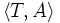$\langle T,A \rangle$ , où $T$ est un ensemble de formules relatives aux informations terminologiques (la T-Box) et $A$ est un ensemble de formules relatives aux informations sur les assertions (la A-Box).

Une autre manière de voir la séparation entre ces informations, est d'associer la T-Box aux règles qui régissent notre monde (e.g., la physique, la chimie, la biologie, ...), et d'associer les individus de notre monde à la A-Box (e.g., Jean, Marie, un chat, ...).

La sémantique

Les logiques de description utilisent les notions de concept, de rôle et d'individu. Les concepts correspondent à des "classes d'éléments" et sont interprétés comme un ensemble dans un univers donné. Les rôles correspondent aux "liens entre les éléments" et sont interprétés comme des relations binaires sur un univers donné. Les individus correspondent aux éléments d'un univers donné. La sémantique des logiques de description est définie comme suit :

Définition 1 :

Soit 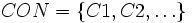$CON = \lbrace C1,C2,\dots \rbrace$ un ensemble fini de concepts atomiques, 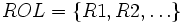$ROL = \lbrace R1,R2,\dots \rbrace$ un ensemble fini de rôles atomiques et 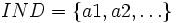$IND = \lbrace a1,a2,\dots \rbrace$ un ensemble fini d'individus. Pour

C O N

R O L

I N D

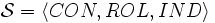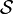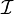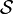disjoint deux à deux, $\mathcal{S} = \langle CON,ROL,IND \rangle$ est une signature. Une fois qu'une signature $\mathcal{S}$ est fixée, une interprétation $\mathcal{I}$ pour $\mathcal{S}$ est un tuple 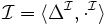$\mathcal{I} = \langle \Delta^\mathcal{I},\cdot^\mathcal{I} \rangle$ , où :

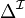$\Delta^\mathcal{I}$ est un ensemble non-vide.
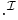est une fonction assignant :
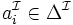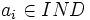- un élément $a_i^\mathcal{I} \in \Delta^\mathcal{I}$ à chaque individu $a_i \in IND$ ;
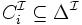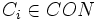- un sous-ensemble $C_i^\mathcal{I} \subseteq \Delta^\mathcal{I}$ à chaque concept atomique $C_i \in CON$ ;
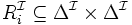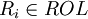- et une relation $R_i^\mathcal{I} \subseteq \Delta^\mathcal{I} \times \Delta^\mathcal{I}$ à chaque rôle atomique $R_i \in ROL$ .

En d'autres mots, une interprétation de la logique de description n'est rien de plus qu'un modèle pour un type particulier de signature du première ordre, où seulement les prédicats unaires et binaires sont autorisés et l'ensemble des symboles de fonctions est vide.

La base de connaissance

Typiquement, la base de connaissance standard utilisée par les logiques de description est définie de la manière suivante :

Définition 2 :

Étant donné un langage de description 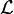$\mathcal{L}$ et une signature 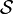$\mathcal{S}$ , une base de connaissance

Σ

dans 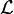$\mathcal{L}$ est une paire 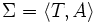$\Sigma = \langle T,A \rangle$ tel que :

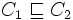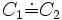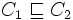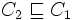$T$ est la T(erminologique)-Box, un ensemble fini, qui peut être vide, d'expressions appelées GCI (General Concept Inclusion) de la forme $C_1 \sqsubseteq C_2$ où $C 1$ et $C 2$ sont des concepts sans restriction. $C_1 \dot{=} C_2$ est une notation pour $C_1 \sqsubseteq C_2$ et $C_2 \sqsubseteq C_1$ . Les formules de $T$ sont appelées des axiomes terminologiques.
$A$ est la A(ssertion)-Box, un ensemble fini, qui peut être vide, d'expressions de la forme $a : C$ ou $(a, b): R$ où $C$ est un concept sans restriction, $R$ un rôle qui n'est pas forcément atomique et $a$ , $b$ appartiennent à $I N D$ . Les formules de $A$ sont appelées des assertions.

Les axiomes terminologiques ont été pensés à l'origine comme une définition, et nombre de conditions plus restrictives ont été imposées. Les deux restrictions les plus importantes sont les suivantes :

axiome terminological simple : dans tous les axiomes terminologiques 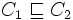$C_1 \sqsubseteq C_2$ , $C 1$ est un concept atomique dans $C O N$ , et chaque concept atomique dans $C O N$ apparaît au plus une fois dans la partie gauche d'un axiome terminologique de la T-Box.
définition acyclique : le graphe obtenu en assignat un nœud $n A$ à chaque concept atomique $A$ de la T-Box, et un arc orienté entre deux nœuds $n A$ et $n B$ s'il existe un axiome terminologique 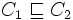$C_1 \sqsubseteq C_2$ dans $T$ tel que $A$ apparaît dans $C 1$ et $B$ dans $C 2$ , ne contienne pas de cycles.

Ces restrictions sont liées à l'idée de considérer les axiomes terminologiques comme des définitions de concepts.

Les différentes logiques de description

Les logiques de descriptions ont une base commune enrichie de différentes extensions (voir tableau ci-dessous). On peut dès lors avoir des concepts complexes composés de concepts atomiques, et de même pour les rôles.

Lettre	Constructeur	Syntaxe	Sémantique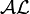
$\mathcal{AL}$	nom de concept	$C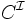$	$C^\mathcal{I}$
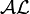
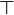
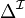
$\mathcal{AL}$	top	$\top$	$\Delta^\mathcal{I}$
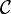
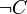
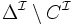
$\mathcal{C}$	négation de concepts non nécessairement primitifs	$\neg C$	$\Delta^\mathcal{I} \setminus C^\mathcal{I}$
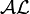
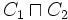
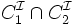
$\mathcal{AL}$	conjonction	$C_1 \sqcap C_2$	$C_1^\mathcal{I} \cap C_2^\mathcal{I}$
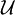
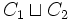
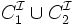
$\mathcal{U}$	disjonction	$C_1 \sqcup C_2$	$C_1^\mathcal{I} \cup C_2^\mathcal{I}$
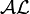
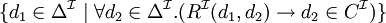
$\mathcal{AL}$	quantificateur universel	$\forall R.C$	$\lbrace d_1\in\Delta^\mathcal{I} \mid \forall d_2 \in \Delta^\mathcal{I}.(R^\mathcal{I}(d_1,d_2) \rightarrow d_2 \in C^\mathcal{I}) \rbrace$
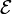
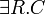
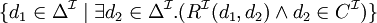
$\mathcal{E}$	quantificateur existentiel typé	$\exists R.C$	$\lbrace d_1\in\Delta^\mathcal{I} \mid \exists d_2 \in \Delta^\mathcal{I}.(R^\mathcal{I}(d_1,d_2) \wedge d_2 \in C^\mathcal{I}) \rbrace$
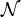
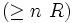
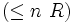
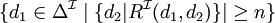
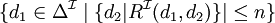
$\mathcal{N}$	restriction de nombre	$(\geq n~R)$ $(\leq n~R)$	$\lbrace d_1\in\Delta^\mathcal{I} \mid \lbrace d_2 \vert R^\mathcal{I}(d_1,d_2) \rbrace \vert \geq n \rbrace$ $\lbrace d_1\in\Delta^\mathcal{I} \mid \lbrace d_2 \vert R^\mathcal{I}(d_1,d_2) \rbrace \vert \leq n \rbrace$
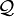
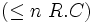
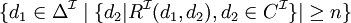
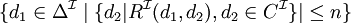
$\mathcal{Q}$	restriction de nombre qualifiée	$(\geq n~R.C)$ $(\leq n~R.C)$	$\lbrace d_1\in\Delta^\mathcal{I} \mid \lbrace d_2 \vert R^\mathcal{I}(d_1,d_2),d_2 \in C^\mathcal{I} \rbrace \vert \geq n \rbrace$ $\lbrace d_1\in\Delta^\mathcal{I} \mid \lbrace d_2 \vert R^\mathcal{I}(d_1,d_2),d_2 \in C^\mathcal{I} \rbrace \vert \leq n \rbrace$
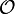
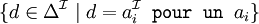
$\mathcal{O}$	un-de	$\lbrace a_1,\dots,a_n \rbrace$	$\lbrace d \in\Delta^\mathcal{I}\mid d = a_i^\mathcal{I} \texttt{~pour~un~} a_i \rbrace$
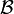
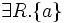
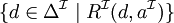
$\mathcal{B}$	role filler	$\exists R.\lbrace a \rbrace$	$\lbrace d \in\Delta^\mathcal{I}\mid R^\mathcal{I}(d,a^\mathcal{I}) \rbrace$
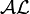
$\mathcal{AL}$	nom de rôle	$R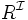$	$R^\mathcal{I}$
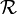
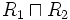
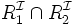
$\mathcal{R}$	conjonction de rôles	$R_1 \sqcap R_2$	$R_1^\mathcal{I} \cap R_2^\mathcal{I}$
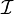
$\mathcal{I}$	rôles inverses	$R - 1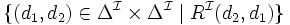$	$\lbrace (d_1,d_2)\in\Delta^\mathcal{I}\times\Delta^\mathcal{I} \mid R^\mathcal{I}(d_2,d_1) \rbrace$
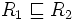
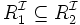
$\mathcal{H}$	hiérarchie des rôles	$R_1\sqsubseteq R_2$	$R_1^\mathcal{I} \subseteq R_2^\mathcal{I}$
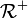
$\mathcal{R^+}$	transitivité des rôles	$R +$	Plus petite relation transitive contenant 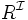$R^\mathcal{I}$

L'une des premières logiques de description est le langage 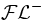$\mathcal{FL^-}$ [Brachman and Levesque, 1984], qui est défini comme une logique de description permettant l'utilisation des quantificateurs universels, de la conjonction, et des quantificateurs existentiels de la forme 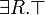$\exists R.\top$ . Le langage 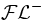$\mathcal{FL^-}$ a été proposé comme un formalisme pour la sémantique des cadres de Minsky. La conjonction de concepts est implicite dans la structure d'un cadre, qui requiert un ensemble de conditions pour être satisfait. La quantification des rôles permet de caractériser les slots.

La logique 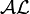$\mathcal{AL}$ [Schmidt-Schauss and smolka, 1991], a étendu la logique 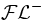$\mathcal{FL^-}$ en y ajoutant la négation des concepts atomiques. Cette logique peut-être considérée comme la logique de base des autres logiques de descriptions.

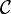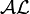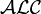Les logiques de description qui existent sont des combinaisons des différents éléments du tableau ci-dessus. Par exemple, si on rajoute la négation complète $\mathcal{C}$ à la logique $\mathcal{AL}$ , on obtient la logique $\mathcal{ALC}$ .

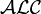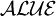Certaines logiques sont équivalentes, notamment $\mathcal{ALC}$ et $\mathcal{ALUE}$ . Ces deux logiques augmentées par 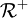$\mathcal{R}^+$ sont notées 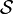$\mathcal{S}$ . Les langages utilisés par OWL en sont une extension, respectivement 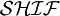$\mathcal{SHIF}$ pour OWL-Lite et 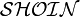$\mathcal{SHOIN}$ pour OWL-DL.

Inférences

En LD, la notion d'inférence est décrite comme ci-dessous:

Définition 3 :

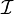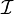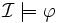Soit $\mathcal{I}$ une interprétation et $\varphi$ un axiome terminologique ou une assertion. Alors $\mathcal{I}$ modélise $\varphi$ (notation $\mathcal{I} \models \varphi$ ) si :

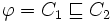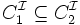$\varphi = C_1 \sqsubseteq C_2$ et $C_1^\mathcal{I} \subseteq C_2^\mathcal{I}$ , ou
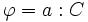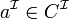$\varphi = a:C$ et $a^\mathcal{I} \in C^\mathcal{I}$ , ou
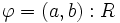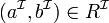$\varphi = (a,b):R$ et $(a^\mathcal{I},b^\mathcal{I}) \in R^\mathcal{I}$ .

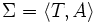Soit $\Sigma = \langle T,A \rangle$ une base de connaissance et 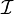$\mathcal{I}$ une interprétation, alors 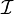$\mathcal{I}$ est un modèle de $Σ$ (notation, 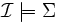$\mathcal{I} \models \Sigma$ ) si pour tous 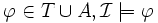$\varphi \in T \cup A, \mathcal{I} \models \varphi$ . Nous disons dans ce cas que 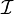$\mathcal{I}$ est un modèle de la base de connaissance $Σ$ . 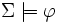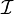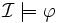Étant donné une base de connaissance $Σ$ et un axiome terminologique ou une assertion $\varphi$ , $\Sigma \models \varphi$ si pour tout modèle $\mathcal{I}$ de $Σ$ nous avons $\mathcal{I} \models \varphi$ .

Les tâches de raisonnement

En LD, l'expression raisonnement sur la T-Box fait référence à la capacité de réaliser des inférences depuis une base de connaissance 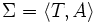$\Sigma = \langle T,A \rangle$ où $T$ est non-vide, et d'une manière similaire, raisonnement sur la A-Box est l'implication pour une A-Box non vide.

Définition 4 :

Soit

Σ

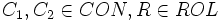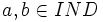une base de connaissances, $C_1,C_2 \in CON, R \in ROL$ et $a,b \in IND$ , nous définissons les tâches de déduction suivantes :

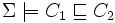
Subsomption, $\Sigma \models C_1 \sqsubseteq C_2$
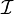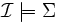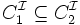Vérifie si pour toutes les interprétations $\mathcal{I}$ tel que $\mathcal{I} \models \Sigma$ , nous avons $C_1^\mathcal{I} \subseteq C_2^\mathcal{I}$ .
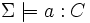
Vérification d'instance, $\Sigma \models a:C$
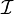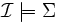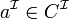Vérifie si pour toutes les interprétations $\mathcal{I}$ tel que $\mathcal{I} \models \Sigma$ , nous avons $a^\mathcal{I} \in C^\mathcal{I}$ .
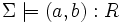
Vérification de relations $\Sigma \models (a,b):R$
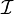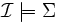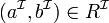Vérifie si pour toutes les interprétations $\mathcal{I}$ tel que $\mathcal{I} \models \Sigma$ , nous avons $(a^\mathcal{I},b^\mathcal{I}) \in R^\mathcal{I}$ .
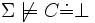
Cohérence de concept, $\Sigma \not \models C \dot{=} \bot$
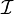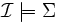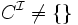Vérifie si pour toutes les interprétations $\mathcal{I}$ tel que $\mathcal{I} \models \Sigma$ , nous avons $C^\mathcal{I} \not = \lbrace \rbrace$ .
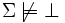
Cohérence de la base de connaissances, $\Sigma \not \models \bot$
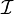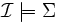Vérifie s'il existe $\mathcal{I}$ tel que, $\mathcal{I} \models \Sigma$ .

Les tâches de déduction de base peuvent être utilisées pour définir des tâches plus complexes. En particulier:

Recherche : étant donné un concept, trouver les individus mentionnés dans la base de connaissance qui sont des instances de ce concept.
Réalisation : étant donné un individu mentionné dans la base de connaissance, trouver le concept le plus spécifique, en accord avec les relations de subsomption, duquel l'individu est une instance.

La saturation de la A-Box sert à compléter les informations de la A-Box en accord avec les connaissances de la T-Box, on obtient donc: Définition 5 :

Étant donné une base de connaissance 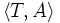$\langle T,A \rangle$ , nous disons que

A

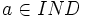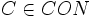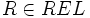est saturé si pour chaque individu $a \in IND$ , concept atomique $C \in CON$ et rôle $R \in REL$ :

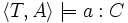
l'assertion $a : C$ si et seulement si $\langle T,A \rangle \models a:C$
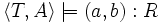
l'assertion $(a, b): R$ si et seulement si $\langle T,A \rangle \models (a,b):R$

Exemple

Soit

Σ

une base de connaissance 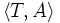$\langle T,A \rangle$ où:

$T = \lbrace \texttt{ETALON} \dot{=} \texttt{CHEVAL} \sqcap \forall \texttt{Sexe.MASCULIN} \rbrace$
$A = \lbrace \texttt{shadowfax}:\texttt{ETALON} \rbrace$

La formule de $T$ dit que les chevaux de sexe masculin sont des étalons, et la formule de $A$ dit que le cheval shadowfax est un étalon. La sémantique formelle que nous donnons dans la définition 3 nous permet de vérifier que $Σ$ a au moins un modèle (i.e., il est cohérent). 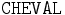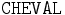Et à partir de $Σ$ nous pouvons déduire plusieurs informations comme, par exemple, que le concept $\texttt{CHEVAL}$ est cohérent avec $Σ$ (il existe une certaine interprétation satisfaisant $Σ$ qui assigne une extension non-vide à $\texttt{CHEVAL}$ :

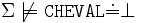
$\Sigma \not \models \texttt{CHEVAL} \dot{=} \bot$

Notons qu'à cause des limitations syntaxiques dans la définition de base des assertions, il n'est pas possible de représenter les implications fortes (qui proviennent de 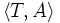$\langle T,A \rangle$ ) telle que par exemple le fait que dans tous les modèles de 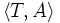$\langle T,A \rangle$ , l'extension de 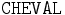$\texttt{CHEVAL}$ est non-vide:

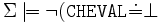$\Sigma \models \neg (\texttt{CHEVAL} \dot{=} \bot$ )

Avec 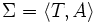$\Sigma = \langle T,A \rangle$ comme connaissance de base on a la A-Box saturé :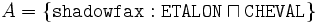

$A = \lbrace \texttt{shadowfax}:\texttt{ETALON} \sqcap \texttt{CHEVAL}\rbrace$

Références

F. Baader, D. Calvanese, D. L. McGuiness, D. Nardi, P. F. Patel-Schneider: The Description Logic Handbook: Theory, Implementation, Applications. Cambridge University Press, Cambridge, UK, 2003. (ISBN 0-52178-176-0)
M.L. Minsky. A Framework for Representing Knowledge. Report A.I MEMO 306, Massachusetts Institute of Technology, A.I. Lab., Cambridge, Massachusetts, juin 1974. McGraw-Hil, P.H. Winston (Éd.), "Psychology of Computer Vision", 1975.

Voir aussi

Liens externes

(en) Description Logics maintenu par Carsten Lutz
(en) 'Introduction to Description Logics DL course par Enrico Franconi, Faculty of Computer Science, Free University of Bozen-Bolzano, Italy
(en) Navigator on Description Logic Complexity
(fr) Une introduction aux logiques de description

Ce document provient de « Logique de description ».

Catégories : Logique | Informatique théorique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Logique De Description de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Logique de description — Les logiques de description aussi appelé logiques descriptives (LDs) sont une famille de langages de représentation de connaissance qui peuvent être utilisés pour représenter la connaissance terminologique d un domaine d application d une manière … Wikipédia en Français
Logique descriptive — Logique de description Les logiques de description aussi appelé logiques descriptives (LDs) sont une famille de langages de représentation de connaissance qui peuvent être utilisés pour représenter la connaissance terminologique d un domaine d… … Wikipédia en Français
Logique (mathématiques) — Logique mathématique La logique mathématique est née à la fin du XIXe siècle de la logique au sens philosophique du terme. Ses débuts furent marqués par la rencontre entre deux idées nouvelles : la volonté chez Frege, Russell, Peano et… … Wikipédia en Français
Logique Mathématique — La logique mathématique est née à la fin du XIXe siècle de la logique au sens philosophique du terme. Ses débuts furent marqués par la rencontre entre deux idées nouvelles : la volonté chez Frege, Russell, Peano et Hilbert de donner une … Wikipédia en Français
Logique mathematique — Logique mathématique La logique mathématique est née à la fin du XIXe siècle de la logique au sens philosophique du terme. Ses débuts furent marqués par la rencontre entre deux idées nouvelles : la volonté chez Frege, Russell, Peano et… … Wikipédia en Français
Logique — Pour les articles homonymes, voir Logique (homonymie). Gregor Reisch« La logique présente ses thèmes centraux », Margarita Philosophica, 1503/08 … Wikipédia en Français
Logique mathématique — La logique mathématique, ou logique formelle, est une discipline des mathématiques introduite à la fin du XIXe siècle et qui s est donnée comme objet l étude des mathématiques en tant que langage. Les objets fondamentaux de la logique… … Wikipédia en Français
DESCRIPTION ET EXPLICATION — Certaines disciplines sont descriptives: astronomie, anatomie, zoologie. Une description peut être plus qu’une simple collection non ordonnée de faits ou de données, l’exemple des taxinomies le montre. La géographie comporte une partie… … Encyclopédie Universelle
LOGIQUE MATHÉMATIQUE — La logique au sens étroit du terme, c’est à dire la logique formelle par opposition à l’épistémologie ou à la théorie de la connaissance, se propose de donner une théorie de l’inférence formellement valide. Elle considère comme valide toute… … Encyclopédie Universelle
Description Définie — Une description définie est une expression de la forme le X, dans laquelle X est un nom commun ou une locution nominale décrivant un individu ou un objet déterminé, et un seul (par exemple, « le premier singe de l espace » ou « le… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Logique De Description