Revêtement (mathématiques)

Revêtement (mathématiques)
Page d'aide sur l'homonymie Pour les articles homonymes, voir Revêtement.
Revêtement du cercle X par une hélice Y, les ensembles disjoints Si sont projetés homéomorphiquement sur U.

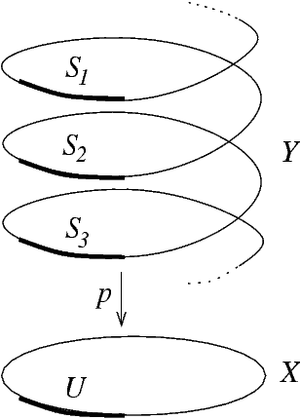
En mathématiques, et plus particulièrement en topologie et en topologie algébrique, un revêtement d'un espace topologique B par un espace topologique E est une application continue et surjective p : E → B telle que tout point b\in B admette un voisinage ouvert U tel que l'image réciproque de U par p soit une union disjointe d'ouverts de E, chacun homéomorphe à U par p.

Il s'agit d'un cas particulier de fibré, localement trivial, à fibre discrète. Les revêtements jouent un rôle pour calculer le groupe fondamental et les groupes d'homotopie d'un espace. Un résultat de la théorie des revêtements est que si B est connexe par arcs et localement simplement connexe, il y a une correspondance bijective entre les revêtements connexes par arcs de B, à isomorphisme près, et les sous-groupes du groupe fondamental de B.

Sommaire

Définition mathématique et terminologie

Homéomorphismes locaux au-dessus de B

Soient X et B deux espaces topologiques.

Un homéomorphisme local[1] est une application continue \pi : X\to B~, appelée projection, telle que pour tout point x de X , il existe un voisinage ouvert U de x et un voisinage ouvert V de π(x) tels que la restriction de π à l'ouvert U soit un homéomorphisme sur V.

Un espace X muni d'un homéomorphisme local \pi : X\to B~ est dit étalé[2] au-dessus de B. L'espace d'arrivée (B) de la projection est appelé la base de l'homéomorphisme local.

Pour tout point b\in B, on appelle fibre de X au-dessus du point b et on note X(b) le sous espace \pi^{-1}(b)\subset X.

On appelle section (continue) de π[1], ou de X, au-dessus de B, une application continue \sigma : B\to X~ telle que \pi\circ\sigma = Id_B.

Par exemple, une submersion entre variétés différentielles de même dimension est un homéomorphisme local.

Conséquences de la définition :

  • un homéomorphisme local est une application ouverte et continue[1],
  • une section est une application injective et continue[1].

Revêtements

Un revêtement d'un espace topologique B est un espace X, muni d'un homéomorphisme local \pi : X\to B~ surjectif, tel que si b est un point de B, il existe un voisinage V de b, un espace discret F (non vide) et un homéomorphisme \Phi : \pi^{-1}(V)\to V\times F~ qui commute avec les projections sur l'espace B, c'est-à-dire que si f\in F, π(Φ − 1(b,f)) = b.

La définition précédente est celle d'un fibré, localement trivial, à fibre discrète avec la remarque que si la base B n'est pas connexe, la fibre F dépend du point base b et s'identifie à la fibre π − 1(b).

Chaque application b\mapsto \Phi^{-1} (b,f) est une section de π − 1(V) au-dessus de l'ouvert V. Autrement dit {\pi}^{-1}(V)~ est la réunion disjointe des ouverts V_f=\Phi^{-1} (V\times f)~ tous homéomorphes par π à V.

Théorème : Soit p un homéomorphisme local dont toutes les fibres sont finies de même cardinal n (non nul), alors p est un revêtement fini.

Revêtements triviaux

Si F est un espace discret, l'application (b,f)\mapsto b définit un revêtement B\times F \to B~ au-dessus de B. Plus généralement, un revêtement est dit trivial si on peut prendre V=B dans la définition, c'est-à-dire s'il existe un espace discret F et un homéomorphisme \Phi : X\to B\times F~ qui commute avec les projections sur l'espace B, c'est-à-dire que si f\in F, π(Φ − 1(b,f)) = b. Un homéomorphisme est un exemple de revêtement trivial.

Exemples

Revêtement du cercle par une droite

Soit S1 le cercle dans le plan \mathbb{R}^2=\mathbb{C}. La droite réelle \mathbb{R} est alors un revêtement de S1 défini par l'application :

p : \mathbb{R} \to S^1, \quad p(t)=(\cos(2\pi t), \sin(2\pi t))=e^{2i\pi t}.

Chaque fibre est ici infinie dénombrable (p^{-1}(p(x))=x+\mathbb{Z}).

La construction se généralise au revêtement exponentiel du tore : \mathbb{R}^n\to \mathbb{T}^n=\mathbb{S}^1\times\mathbb{S}^1\times\ldots\times\mathbb{S}^1\subset \mathbb{R}^{2n}

La fibre est dénombrable : (p^{-1}(0)=\mathbb{Z}^n).

Les fonctions puissances

L'application p du plan complexe privé de l'origine \mathbb{C}^*

p : \mathbb{C}^*\to \mathbb{C}^*, \quad p(z)=z^n définit un revêtement.

Chaque fibre est ici finie et a n élements.

L'application exponentielle

L'application p = exp  du plan complexe \mathbb{C}

p : \mathbb{C}\to \mathbb{C}^*, \quad p(z)=e^z définit un revêtement.

Chaque fibre est ici infinie dénombrable (p^{-1}(p(x))=x+2i\pi\mathbb{Z}).

Revêtement à deux feuillets du ruban de Möbius, homéomorphe à un cylindre. Le ruban de Möbius vient se glisser entre les deux feuillets.

La bande de Möbius

Article détaillé : Ruban de Möbius.

Le cylindre (ou anneau) \mathbb{S}^1\times [0; 1] est un revêtement à deux feuillets de la bande de Möbius.

La bande de Möbius est une variété topologique non orientable alors que son revêtement est orientable. On montre plus généralement que tout variété connexe non orientable possède un revêtement connexe à deux feuillets orientable. C'est le cas notamment du plan projectif dont le revêtement est une sphère (voir ci-dessous), et de la bouteille de Klein dont le revêtement est le tore.

Revêtement de l'espace projectif

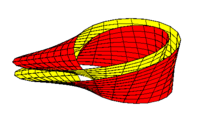
Pour n>1, l'application canonique \mathbb{S}^n\to\mathbb{RP}^n est un revêtement de l'espace projectif (réel) ; la fibre a deux éléments.

Dans le cas du plan projectif dont une représentation dans \mathbb R^3 est donnée par la surface de Boy, il est possible de transformer la sphère par immersion en un revêtement à deux feuillets de cette surface de Boy. Si on fait se traverser ces deux feuillets, on procède alors à un retournement de la sphère[3].

On procède de même pour le retournement du tore, après avoir fait coïncider celui-ci en un revêtement à deux feuillets de la bouteille de Klein.

Constructions de revêtements

Produit fibré, Somme directe, Changement de base

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue !

Soit X, Y et Z trois espaces topologiques, φ un morphisme (application continue) de X dans Z et ψ de Y dans Z. On appelle produit fibré de X et Y par rapport à Z, noté X \otimes _ Z Y, un espace topologique, X \otimes _ Z Y, un morphisme, pX, de ce produit dans X et pY de ce produit dans Y tels que pour tout espace topologique, A et deux morphismes, f (de A dans X) et g (de A dans Y) tels que \varphi \circ f = \psi \circ g, alors il existe un morphisme, pA de A dans le produit, tel que p _ X \circ p _ A = f et p _ Y \circ p _ A = g.

Article détaillé : Produit fibré.

Groupes discrets opérant proprement et librement

Soit G un groupe discret opérant proprement et librement sur un espace localement compact E, la projection E\to E/G~ définit un revêtement de fibre G.

En particulier, si \Gamma~ est un sous-groupe discret du groupe topologique G, la projection G\to G/\Gamma~ est un revêtement de fibre \Gamma~.

Construction de revêtements par recollement

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue !

Théorie des revêtements

Morphismes et transformations de revêtements

Un morphisme de revêtements au-dessus de B est une application continue f : X\to X'~ (où X et X' sont des revêtements) qui commute avec les projections πX et πX', c'est-à-dire telle que :

\pi_{X'}\circ f=\pi_X

.

Les applications identiques IdX sont des morphismes de revêtements.
La composée de deux morphismes de revêtements est un morphisme.

Par conséquent, les revêtements de base B avec leurs morphismes forment une catégorie Rev_B~.

Revêtements sur un segment

Théorème — Tout revêtement sur un intervalle compact [a;b] de R est trivial.

C'est un cas particulier du théorème plus général :

Théorème — Tout espace fibré, localement trivial, sur un intervalle compact [a;b] de R est trivial.

Relèvement des chemins

Proposition — Soit (X,π) un revêtement de B, b un point de B, soit x\in X(b). Soit c un chemin d'origine b Alors il existe un chemin \tilde{c} et un seul dans X d'origine x tel que \pi\circ \tilde{c}=c.

Monodromie des lacets et relèvement des applications

Le groupe fondamental de la base, \pi_1(B,b)~, opère par une action de groupe à droite sur la fibre X(b)=\pi^{-1}(b)~.

Revêtements galoisiens et groupe de Galois d'un revêtement

Un revêtement est dit galoisien (ou régulier ou normal) s'il est connexe par arcs et le groupe des automorphismes agit transitivement sur la fibre de chaque point.

Revêtements universels

Un revêtement universel d'un espace B est un revêtement galoisien E tel que tout revêtement soit isomorphe à un revêtement associé à E (non nécessairement connexe). C’est-à-dire que pour tout revêtement D de B, il existe un morphisme de E sur D.

Deux revêtements universels sont isomorphes et tout revêtement d'un revêtement universel est trivial.

Théorème — Un revêtement simplement connexe E est un revêtement universel.

Théorème — Un espace (connexe par arcs) B admet un revêtement simplement connexe si et seulement s'il est semi-localement simplement connexe.

En particulier tout graphe, toute variété topologique admet un revêtement simplement connexe.

Classification des revêtements et théorie de Galois

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue !

Applications

Graphes et groupes libres

Théorème de Nielsen-Schreier — Tout sous-groupe d'un groupe libre est un groupe libre.

théorème de Van Kampen

Article détaillé : théorème de Van Kampen.

Revêtements ramifiés et surfaces de Riemann

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue !

Revêtements des groupes topologiques

Article détaillé : Revêtement de groupe (en).
Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue !

Bibliographie (en français)

  • Adrien Douady et Régine Douady, Algèbre et théories galoisiennes [détail des éditions]
  • Claude Godbillon, Éléments de topologie algébrique [détail des éditions]
  • Pierre Dolbeault (de), Analyse complexe
  • Jean Dieudonné, Eléments d'Analyse, tome 3

Notes et références

  1. ↑ a, b, c et d Claude Godbillon, Éléments de topologie algébrique [détail des éditions], 1971, p. 105.
  2. ↑ Adrien Douady et Régine Douady, Algèbre et théories galoisiennes [détail des éditions]
  3. ↑ Bernard Morin et Jean-Pierre Petit, Le retournement de la sphère, Les Progrès des mathématiques, Pour la Science, Belin, 1981 ISBN 2-902918-14-3, p. 32–45

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Revêtement (mathématiques) de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Revetement (mathematiques) — Revêtement (mathématiques) Pour les articles homonymes, voir Revêtement. Revêtement du cercle X par une hélice Y, les ensembles disjoints …   Wikipédia en Français

  • Revêtement (mathématique) — Revêtement (mathématiques) Pour les articles homonymes, voir Revêtement. Revêtement du cercle X par une hélice Y, les ensembles disjoints …   Wikipédia en Français

  • Revêtement galoisien — Revêtement (mathématiques) Pour les articles homonymes, voir Revêtement. Revêtement du cercle X par une hélice Y, les ensembles disjoints …   Wikipédia en Français

  • Revêtement universel — Revêtement (mathématiques) Pour les articles homonymes, voir Revêtement. Revêtement du cercle X par une hélice Y, les ensembles disjoints …   Wikipédia en Français

  • Revetement — Revêtement Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. D une manière générale, le mot revêtement peut désigner l action de revêtir quelque chose ou son résultat. Il est employé dans plusieurs… …   Wikipédia en Français

  • Revêtement — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. D une manière générale, le mot revêtement peut désigner l action de revêtir quelque chose ou son résultat. Il est employé dans plusieurs domaines :… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • GROUPES (mathématiques) - Groupes de Lie — La théorie des groupes de Lie, fondée dans la période de 1870 1880 par le mathématicien norvégien Sophus Lie, a d’abord été considérée comme une partie assez marginale des mathématiques, liée à des problèmes touchant les équations différentielles …   Encyclopédie Universelle

  • Anneau de Möbius — Ruban de Möbius Pour les articles homonymes, voir Moebius. Réalisation à partir d une bande de papier En topologie, le r …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”