Theoreme de van Kampen

Theoreme de van Kampen

Théorème de van Kampen

En topologie algébrique, le théorème de van Kampen, également appelé théorème de Seifert-Van Kampen, est un résultat permettant de calculer le groupe fondamental d'un espace topologique qui se décompose en des espaces plus simples dont les groupes fondamentaux sont déjà connus.

Sommaire

Énoncé

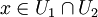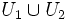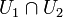Soient U1, U2 des ouverts connexes par arcs ainsi que leur intersection, et soit x \in U_1 \cap U_2. Alors le groupe fondamental de U_1 \cup U_2 en x est égal à la somme amalgamée[1] de la famille des groupes fondamentaux de U1 et U2 au-dessus de celui de U_1 \cap U_2 :

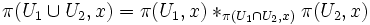\pi(U_1 \cup U_2, x) = \pi(U_1, x) *_{\pi(U_1 \cap U_2, x)} \pi(U_2,x).

Un cas particulier essentiel est celui où 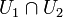U_1 \cap U_2 est simplement connexe : 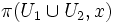\pi(U_1 \cup U_2, x) est alors le produit libre π(U1,x) * π(U2,x) des groupes fondamentaux de U1 et U2.

Par exemple, un tore percé d'un trou est homéomorphe à la réunion de deux cylindres d'intersection simplement connexe. Le théorème de van Kampen montre que son groupe fondamental est 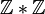\mathbb Z* \mathbb Z, c'est à dire le groupe libre sur deux générateurs. De façon similaire, le groupe fondamental du plan projectif est le groupe à deux éléments.

Cas de deux sous-espaces fermés

Le théorème énoncé ci-dessus reste valide si U1, U2 et 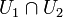U_1\cap U_2 sont des sous-espaces fermés connexes par arcs[2].

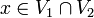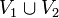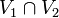Soient V1, V2 des sous-espaces fermés connexes par arcs qui admettent des revêtements simplement connexes, ainsi que leur intersection, et soit x \in V_1 \cap V_2. Alors le groupe fondamental de V_1 \cup V_2 en x est égal à la somme amalgamée de la famille des groupes fondamentaux de V1 et V2 au-dessus de celui de V_1 \cap V_2 :

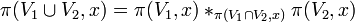\pi(V_1 \cup V_2, x) = \pi(V_1, x) *_{\pi(V_1 \cap V_2, x)} \pi(V_2,x).

Notes et références

  1. ↑ Michel Zisman, Topologie algébrique élémentaire ; N. Bourbaki, Algèbre, chapitre I, pages I.80-84, A. Douady, Algèbre et théories galoisiennes, 2e édition, page 252 (la somme amalgamée était appelée produit libre amalgamé dans le tome 2 de la première édition)
  2. ↑ A. Douady, Algèbre et théories galoisiennes, tome 2, qui suppose que les espaces admettent un revêtement universel pointé.

Bibliographie

  • Michel Zisman, Topologie algébrique élémentaire, ed. Armand Colin
  • A. Douady, Algèbre et théories galoisiennes, première édition, ed. Cedic/Fernand Nathan et deuxième édition, ed. Cassini.
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de van Kampen ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de van Kampen de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Théorème de Van Kampen — En topologie algébrique, le théorème de van Kampen, également appelé théorème de Seifert Van Kampen, est un résultat permettant de calculer le groupe fondamental d un espace topologique qui se décompose en des espaces plus simples dont les… …   Wikipédia en Français

  • Théorème de van kampen — En topologie algébrique, le théorème de van Kampen, également appelé théorème de Seifert Van Kampen, est un résultat permettant de calculer le groupe fondamental d un espace topologique qui se décompose en des espaces plus simples dont les… …   Wikipédia en Français

  • Théorème de van Kampen — En topologie algébrique, le théorème de van Kampen (en), également appelé théorème de Seifert (en) Van Kampen, est un résultat permettant de calculer le groupe fondamental d un espace topologique qui se décompose en des espaces plus… …   Wikipédia en Français

  • Groupe fondamental — Pour les articles homonymes, voir Groupe de Poincaré. En mathématiques, et plus spécifiquement en topologie algébrique, le groupe fondamental, ou groupe de Poincaré, est un invariant topologique. Le groupe fondamental d un espace topologique… …   Wikipédia en Français

  • Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Liste des theoremes — Liste des théorèmes Liste des théorèmes par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le… …   Wikipédia en Français

  • Liste des théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Revetement (mathematiques) — Revêtement (mathématiques) Pour les articles homonymes, voir Revêtement. Revêtement du cercle X par une hélice Y, les ensembles disjoints …   Wikipédia en Français

  • Revêtement (mathématique) — Revêtement (mathématiques) Pour les articles homonymes, voir Revêtement. Revêtement du cercle X par une hélice Y, les ensembles disjoints …   Wikipédia en Français

  • Revêtement (mathématiques) — Pour les articles homonymes, voir Revêtement. Revêtement du cercle X par une hélice Y, les ensembles disjoints Si sont projeté …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”