Groupe Libre

Le groupe libre sur un ensemble S est le groupe F contenant S et caractérisé par la propriété universelle suivante : pour tout groupe G et toute application ensembliste f de S dans G, il existe un unique morphisme de groupe de F dans G prolongeant f.

Soit encore, un groupe G est dit libre s'il existe un sous-ensemble S de G tel que chaque élément de G puisse être écrit d'une unique façon sous la forme d'un produit d'un nombre fini d'éléments de S et de leur inverse. Un tel groupe est unique à isomorphisme près ce qui jusitifie le qualificatif le dans la définition. En général, on le notera F_S ou L(S). Intuitivement, F_S est le groupe engendré par S sans relation entre les éléments de S.

Attention : cette notion diffère de celle de groupe abélien libre.

Sommaire 1 Histoire 2 Construction 3 Premières propriétés 4 Exemples 5 Sous-groupes d'un groupe libre 6 Référence

Histoire

Walther von Dyck étudie en 1882 le concept de groupe libre, sans y donner de nom, dans son article Gruppentheoretishe Sudien (Étude de la théorie des groupes) publié dans Mathematische Annalen (annales mathématiques). Le terme de groupe libre a été introduit par Jakob Nielsen en 1924.

Construction

Introduisons un ensemble S' équipotent à S et disjoint de S. Il existe alors une bijection de S vers S'. Pour chaque élément s de S, on note s' l'élément correspondant dans S'.

Notons M l'ensemble des mots sur la réunion de S et de S', c'est-à-dire les chaînes finies de caractères constituées d'éléments de S et de S'. Deux telles chaînes seront dites équivalentes si on peut passer de l'une à l'autre en enlevant ou en rajoutant des chaînes de la forme ss' ou s's. Ceci définit une relation d'équivalence R sur M. On définit F_S comme l'ensemble des classes d'équivalence modulo R. On identifie chaque élément s de S avec sa classe dans F_S pour avoir l’inclusion .

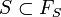La concaténation de deux mots définit une loi sur M préservée par l'équivalence. Par passage au quotient, on obtient un loi de groupe sur F_S. L'élément neutre est la classe du mot vide, et l'inverse de la classe de est la classe de .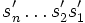

Vérification de la propriété universelle : Si G est un groupe, toute application ensembliste 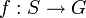se prolonge en un morphisme de monoïdes 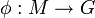défini par. Ce morphisme est constant sur les classes d'équivalence, et induit donc un morphisme de groupes 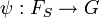qui prolonge f.

Premières propriétés

• Si S et T ont même cardinal, alors F_S et F_T sont isomorphes. En effet, une bijection entre S et T donne lieu à des morphismes de F_S dans F_T et de F_T dans F_S, morphismes qui sont réciproques l'un de l'autre. Réciproquement, si F_S et F_T sont isomorphes, on peut montrer que S et T ont même cardinal. D’ailleurs, si S est infini, F_S a le même cardinal que S.
• Soit G un groupe, et soit S un système générateur de G. Alors G est un quotient du groupe libre F_S sur S. En particulier, n’importe quel groupe est le quotient d'un groupe libre, d’où la notion de présentation d'un groupe (par générateurs et relations).

Exemples

• Le groupe libre sur l'ensemble vide est le groupe trivial, et le groupe libre sur un singleton est isomorphe à 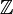. Ce sont les deux seuls groupes libres commutatifs.

• Soit n un entier naturel. Le groupe fondamental du plan privé de n points est un groupe libre sur un ensemble de cardinal n.

Sous-groupes d'un groupe libre

• Les sous-groupes d'un groupe libre sont libres (Théorème de Nielsen-Schreier). La démonstration de ce résultat n'est pas immédiate^[1].
• Le groupe libre à 2 générateurs F_{a,b} contient la famille libre infinie 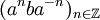, et le sous-groupe engendré par cette dernière n’admet aucun système fini de générateurs.

Ainsi, on n’a pas d’analogue non abélien du résultat suivant : tout sous-groupe d'un groupe abélien libre de type fini est un sous-groupe abélien libre de type fini.

Référence

• (en) Marshall Hall, The theory of groups [détail des éditions], chapitre 7.

• Portail des mathématiques