Groupes d'homotopie

Groupes d'homotopie

Groupe d'homotopie

En mathématiques, et plus particulièrement en topologie et topologie algébrique, les groupes d'homotopie sont des invariants qui généralisent la notion de groupe fondamental aux dimensions supérieures.

Sommaire

Définition mathématique

Il y a plusieurs définitions équivalentes possibles. La première définition :

Soit X un espace topologique et x0 un point de X. Soit 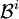\mathcal{B}^i la boule unité de dimension i de l'espace euclidien 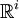\mathbb{R}^i. Son bord 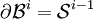\partial \mathcal{B}^i = \mathcal{S}^{i-1} est la sphère unité de dimension i − 1.

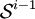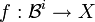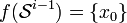Le i-ième groupe d'homotopie supérieur πi(X,x0) est l'ensemble des classes d'homotopie relative à \mathcal{S}^{i-1} d'applications continues f : \mathcal{B}^i\to X telle que : f(\mathcal{S}^{i-1}) = \{x_0\}.

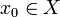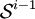Un élément de πi(X,x0) est donc représenté par une fonction continue de la i-boule vers X, qui envoie la (i − 1)-sphère vers le point de référence x_0\in X, la fonction étant définie modulo homotopie relative à \mathcal{S}^{i-1}.


La deuxième définition :

En identifiant le bord du disque en un point s0, on obtient une sphère 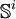\mathbb{S}^i et chaque élément de πi(X,x0) se définit par les classes d'homotopie des applications 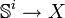\mathbb{S}^i\to X par lesquelles le point base de la sphère s0 se transforme en x0. 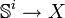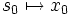On peut dire que les éléments du groupe πi(X,x0) sont les composantes connexes de l'espace topologique des applications \mathbb{S}^i\to X pour lesquelles on a : s_0\mapsto x_0.

Produit sur l'ensemble des classes d'homotopie

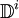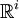Pour définir une opération sur les classes d'homotopie, il est utile d'identifier le disque \mathbb{D}^i avec le cube \mathbb{I}^i=[0; 1]^i de dimension i dans \mathbb{R}^i.

La définition du produit est la suivante : La somme de deux applications du cube 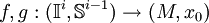f,g : (\mathbb{I}^i,\mathbb{S}^{i-1})\to (M,x_0) est l'application 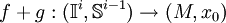f+g : (\mathbb{I}^i,\mathbb{S}^{i-1})\to (M,x_0) définie par la formule :

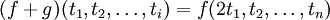(f + g)(t_1, t_2,\ldots, t_i) = f(2t_1, t_2, \ldots, t_n) pour t_1\in [0 ; {1\over 2}]

et

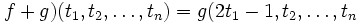(f + g)(t_1, t_2, \ldots, t_n) = g(2t_1-1, t_2, \ldots, t_n) pour t_1\in [{1\over2} ; 1].

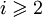Lorsque l'on passe aux classes d'homotopie, la loi de composition obtenue est associative, unifère, tout élément admet un inverse et la loi est commutative si i\geqslant 2.

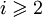On définit donc un groupe commutatif si i\geqslant 2.

On obtient le groupe fondamental si i = 1

Propriétés et outils

Suite exacte longue d'homotopie d'une fibration et fonctorialité

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Groupes d'homotopie relatifs et suite exacte longue d'homotopie d'un couple

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Homologie et homotopie : le théorème de Hurewicz

Pour un espace topologique X, on a deux familles de groupes associés à X : Les groupes d'homotopie (relatifs) notés πi(X,A,x0) et les groupes d'homologie singulière (relatifs) notés Hi(X,A). Les groupes d'homologie sont plus faciles à calculer que les groupes d'homotopie, et on s'interroge sur le liens entre ces deux familles de groupes.

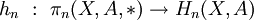On a un morphisme de groupes naturel h_n\ :\ \pi_n(X,A,*)\to H_n(X,A).


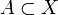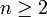Si A\sub X sont connexes par arcs et si le couple (X,A) est n-1-connexe, n\geq 2,

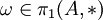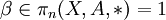le théorème de Hurewicz relatif affirme que Hi(X,A) = 0 (i<n) et que le morphisme de Hurewicz est un épimorphisme dont le noyau est engendré par les éléments ω(β) − β avec \omega\in\pi_1(A,*) et \beta\in\pi_n(X,A,*)=1. En particulier, si π1(A, * ) = 1, alors hn est un isomorphisme.

Le théorème de Hurewicz absolu (A=*) affirme que si X est n-1-connexe, 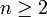n\geq 2, on a Hi(X, * ) = 0 (i<n) et que le morphisme de Hurewicz est un isomorphisme.

Pour n=1, voir Théorème d'Hurewicz

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Le théorème de Whitehead pour les CW-complexes (complexes cellulaires)

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Théorèmes de périodicité de Bott

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Espaces asphériques, espaces d'Eilenberg MacLane et théorie de l'obstruction

Un espace est dit asphérique ou un K(π,1) si les groupes d'homotopies sont triviaux sauf le π1

Méthodes de calcul

Contrairement au groupe fondamental (i=1) et aux groupes d'homologie et de cohomologie, il n'y a pas de méthode simple de calcul des groupes d'homotopie dès que 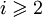i\geqslant 2 (Il manque un analogue des théorèmes d'excision et de Van-Kampen).

Groupes d'homotopie des sphères

Article détaillé : Groupes d'homotopie des sphères.

Cas des groupes de Lie

Le groupe fondamental est commutatif. L'action du π1 sur les πi est triviale.

Bibliographie en français

  • Doubrovine, Novikov, Fomenko : Géométrie contemporaine, tomes 2 et 3, ed. Mir (Moscou)
  • Jean Dieudonné : Eléments d'analyse, tome 9, ed. Jacques Gabais
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Groupe d%27homotopie ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Groupes d'homotopie de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Groupes D'homotopie Des Sphères — En mathématiques, et plus spécifiquement en topologie algébrique, les groupes d homotopie des sphères sont des invariants qui décrivent, en termes algébriques, comment des sphères de dimensions égales ou différentes peuvent s enrouler l une sur l …   Wikipédia en Français

  • Groupes d'homotopie des spheres — Groupes d homotopie des sphères En mathématiques, et plus spécifiquement en topologie algébrique, les groupes d homotopie des sphères sont des invariants qui décrivent, en termes algébriques, comment des sphères de dimensions égales ou… …   Wikipédia en Français

  • Groupes d'homotopie des sphères — Enroulement d une sphère à deux dimensions autour d une autre sphère En mathématiques, et plus spécifiquement en topologie algébrique, les groupes d homotopie des sphères sont des invariants qui décrivent, en termes algébriques, comment des… …   Wikipédia en Français

  • GROUPES (mathématiques) - Groupes de Lie — La théorie des groupes de Lie, fondée dans la période de 1870 1880 par le mathématicien norvégien Sophus Lie, a d’abord été considérée comme une partie assez marginale des mathématiques, liée à des problèmes touchant les équations différentielles …   Encyclopédie Universelle

  • Homotopie — Les deux jeux de lettres : bleu et rouge, peuvent être définis par des fonctions homotopes. L homotopie est une notion de topologie algébrique. Elle formalise la notion de déformation continue d un objet à un autre. Deux lacets sont dits… …   Wikipédia en Français

  • GROUPES (mathématiques) — LES IDÉES de symétrie et de régularité se retrouvent dans toutes les civilisations, bien avant que ne fût conçue la notion de groupe: par exemple, presque tous les groupes discrets de déplacements du plan (il y en a dix sept types non isomorphes) …   Encyclopédie Universelle

  • Groupe d'homotopie — En mathématiques, et plus particulièrement en topologie et topologie algébrique, les groupes d homotopie sont des invariants qui généralisent la notion de groupe fondamental aux dimensions supérieures. Sommaire 1 Définition mathématique 2 Produit …   Wikipédia en Français

  • TOPOLOGIE - Topologie algébrique — Inventée au début du XXe siècle pour résoudre des problèmes géométriques, la topologie algébrique connut un grand développement grâce à l’introduction de constructions algébriques de plus en plus abstraites. Pour clarifier l’exposé, on a… …   Encyclopédie Universelle

  • Groupe fondamental — Pour les articles homonymes, voir Groupe de Poincaré. En mathématiques, et plus spécifiquement en topologie algébrique, le groupe fondamental, ou groupe de Poincaré, est un invariant topologique. Le groupe fondamental d un espace topologique… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”